Python 解决数学问题-SymPy库的使用

王茂南

3045
文章

75
评论

2021年3月27日07:39:17

评论 3378字阅读11分15秒

摘要本文会介绍 Python 中的 SymPy 库。该库可以用来进行一些数学运算。本文会根据五个例子（分别是解方程，求极限，求积分，解微分方程，矩阵运算）来简单说明 SymPy 的功能。

文章目录(Table of Contents)

简介

本章会介绍使用 SymPy 来解决一些数学问题，包括解方程组，解决微积分的相关问题，化简矩阵。SymPy 是一个符号数学的 Python 库（符号计算）。它的目标是成为一个全功能的计算机代数系统，同时保持代码简洁、易于理解和扩展。 SymPy 完全是用 Python 写的，并不需要外部的库。

首先我们使用 pip 来安装 SymPy 库：

sudo pip3 install sympy

本节的内容会从下面的五个例子来进行说明，对 SymPy 有一个大致的了解：

使用 SymPy 库解线性方程组;
使用 SymPy 库求极限;
使用 SymPy 来计算积分（包含定积分和不定积分）;
使用 SymPy 库解微分方程;
使用 SymPy 库化简矩阵;

参考资料

SymPy, 官网的相关说明；
使用 Python 解数学方程，主要参考自这个教程；

SymPy 的简单例子

使用 SymPy 解决线性方程

首先我们使用 SymPy 来解决线性方程。这里使用下面的方程组来作为例子，一共有三个未知数，分别为 x、y、z。

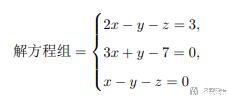
我们使用 SymPy 来解上面的方程组。完整的代码如下所示，我们首先定义三个变量，接着使用 SymPy 中的 solve 来解出上面的方程组。

from sympy import Symbol, solve
# 定义变量
x = Symbol(’x’)
y = Symbol(’y’)
z = Symbol(’z’)
# 解线性方程组
result = solve([2 * x - y - z - 3, 3 * x + y - 7, x - y -z],[x, y, z])
print(result)
"""
{x: 3, y: -2, z: 5}
"""

其中 solve 中的第一个参数为要解的方程，这里要求右端等于 0；例如上面的第一个式子 2x − y − z = 3, 我们需要修改为 2x − y − z − 3 = 0。第二个参数为要解的未知数。

最终上面的方程组的解为如下所示：

使用 SymPy 求极限

第二个例子我们使用 SymPy 来求极限。我们使用下面的作为例子，求下面极限的结果：

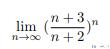
使用 SymPy 中的 limit 来求上面的极限。完整的代码如下所示：

from sympy import Symbol, limit, oo
n = Symbol(’n’)
s = ((n+3)/(n+2))**n # 定义极限的式子
# 求极限, 计算 n 在 oo (正无穷) 的极限
limit_value = limit(s, n, oo)
print(limit_value)
"""E
"""

这里对上面的 limit 函数进行简单的解释：

这里 limit ：
- 第一个输入 s 为式子（要求极限的式子）
- 第二和第三个表示变量 n 在 ∞ 时式子 s 的值;
oo (两个字母 o) 表示无穷大，这个也是要从 sympy 中进行 import 的;
E 表示常数 e;

使用 SymPy 求积分

第三个例子我们使用 SymPy 来求积分。这里我们会分别来看计算定积分和不定积分。首先看一个不定积分的例子，我们口算可以得到积分结果是 x^6，我们使用 SymPy 计算以一下结果是否相同。

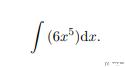
具体来讲，我们使用 SymPy 中的 integrate 来验证一下结果是否正确。具体的代码如下所示，最终的结果和我们计算得到的相同。

from sympy import Symbol, integrate
# 不定积分
x = Symbol(’x’)
print(integrate(6*x**5, x))
"""x**6
"""

接下来看一下求解定积分，看下面的例子：

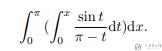
我们还是首先定义变量 x 和 t，接着计算小括号里面的式子（得到关于 x 的函数），最后再计算整个式子。完整的代码如下所示，需要注意这里 sin 函数和常数 π 需要提前从 SymPy 中 import 进来：

from sympy import Symbol, integrate, sin, pi
t = Symbol(’t’)
x = Symbol(’x’)
f_x = integrate(sin(t)/(pi-t), (t, 0, x))
print(f_x)
"""Si(x - pi) + Si(pi)
"""
print(integrate(f_x, (x, 0, pi)))
"""2
"""

最终的定积分的结果为 2。上面中间结果中的 Si(x) 是菲涅耳正弦积分。

使用 SymPy 求微分方程

第四个例子我们尝试使用 SymPy 来求解微分方程。在求解微分方程之前，我们首先看一下如何使用 SpmPy 来进行求导操作。

使用 SymPy 求导

下面分别使用 SpmPy 来求一阶导和二阶导。

from sympy import Function, Symbol, diff
# 使用 sympy 进行求导
x = Symbol(’x’)
print(diff(x**3, x, 1)) # 一阶导数
"""3*x**2
"""
print(diff(x**3, x, 2)) # 二阶导数
"""6*x
"""

使用 SymPy 解微分方程

在了解如何使用 SymPy 如何求导之后，我们来解下面的微分方程。

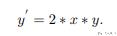
我们使用 dsolve 函数来解决微分方程（differential equation）。需要注意的是，上面的 y 是一个关于 x 的式子，即可以写成 y(x)。在 SymPy 中，关于 x 的函数可以使用 Function 来定义。完整的代码如下所示：

from sympy import Function, Symbol, diff, dsolve
y = Function(’y’)
x = Symbol(’x’)
print(dsolve(diff(y(x),x) - 2*y(x)*x, y(x)))
"""Eq(y(x), C1*exp(x**2))
"""

使用 SymPy 进行矩阵运算

第五个例子尝试使用 SymPy 来解决线性代数中的问题。例如我们想要完成以下的矩阵运算：

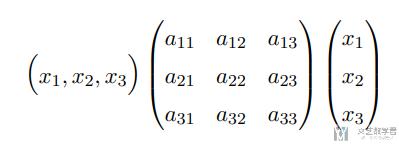
在 SymPy 中，矩阵可以使用 Matrix 来进行定义。例如 (x1, x2, x3) 可以按下面这样定义：

from sympy import symbols, Matrix
# 矩阵的定义
x1, x2, x3 = symbols(’x1␣x2␣x3’)
m = Matrix([[x1, x2, x3]])
print(m)
"""Matrix([[x1, x2, x3]])
"""

知道了矩阵如何定义之后，我们就可以对上面的矩阵运算进行化简。完整的代码如下所示：

from sympy import symbols, Matrix
# 矩阵的定义
x1, x2, x3 = symbols('x1 x2 x3')
m = Matrix([[x1, x2, x3]])
print(m)
# 矩阵运算
x1, x2, x3 = symbols('x1 x2 x3')
a11, a12, a13, a21, a22, a23, a31, a32, a33 = symbols('a11 a12 a13 a21 a22 a23 a31 a32 a33')
m = Matrix([[x1, x2, x3]])
print(m)
"""Matrix([[x1, x2, x3]])
"""
a = Matrix([[a11, a12, a13], [a21, a22, a23], [a31, a32, a33]])
print(a)
"""Matrix([[a11, a12, a13], [a21, a22, a23], [a31, a32, a33]])
"""
v = Matrix([[x1],[x2],[x3]])
print(v)
"""Matrix([[x1], [x2], [x3]])
"""
print(m*a*v)
"""Matrix([[x1*(a11*x1 + a21*x2 + a31*x3) + x2*(a12*x1 + a22*x2 + a32*x3) + x3*(a13*x1 + a23*x2 + a33*x3)]])
"""