数据结构与算法基础-开篇

简介

从这一篇开始, 会记录数据结构与算法的相关内容, 每一篇会介绍相关的内容和leetcode上的例题分析. 也是第一次开始写这个, 就慢慢往里面进行补充.

这第一篇, 介绍一下时间复杂度, 包括递归问题的时间复杂度的计算. 最后包含一些常见递归算法的时间复杂度. 最后写一下自己练习的方式, 要每天坚持练习.

时间复杂度

关于时间复杂度, 我们通常使用Big-O来表示程序最坏情况下的时间复杂度. 有下面几种情况.

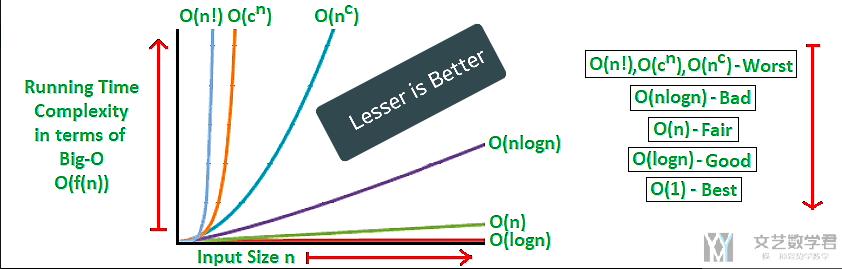
下面对每一种进行一些介绍, 什么情况下会出现.

• O(1)
• O(logn): for (i=1, i<n, i=i*2), 后面会给出详细介绍
• O(n): for循环
• O(n^2): 双重循环
• O(2^n): for中, 包含i<2^n, (i=1, i<2^n, i++)
• O(n!): for中, 包含i<n!, (i=1, i<n!, i++)

关于O(logn)的时间复杂度, 我们在这里多介绍一些, 即为什么(i=1, i<n, i=i*2)的复杂度是logn.

关于递归问题的时间复杂度

关于递归问题的时间复杂度需要使用Master theorem, 参考链接, Master theorem (analysis of algorithms). 我们这里就看一个简单的例子, 使用fibonacci sequence作为例子.

比如我们要计算f(5), 这时候就需要计算f(5)=f(4)+f(3), 最终的递归树如下所示:

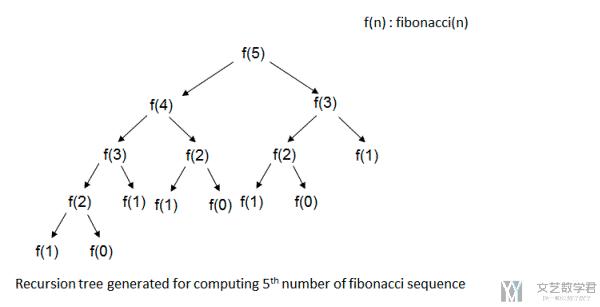
从上面递归树可以看出, 此时需要计算15次. 其实这里大概的次数是2^n, 也就是这里如果使用递归计算, 计算第N个数字, 时间复杂度是O(2^n).

参考资料: Time and Space Complexity of Recursive Algorithms

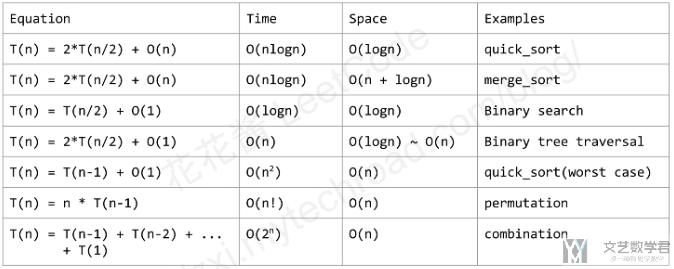
常见递归算法时间复杂度

• Binary search(二分查找): O(logn)
• Binary Tree Traversal(二叉树遍历): O(n)
• Merge Sort(归并排序): O(n*logn)
• Quick Sort(快排): O(n*logn)

练习方式

这个系列的内容都会基于leetcode上的习题, 之后每次记录内容的时候自己也会去leetcode上做题. 在做题的时候, 需要注意下面的点.

• 读题, 注意数据的范围
• 把所有可能的解法都想一下, 综合时间复杂度使用一个最佳的解法
• 做完题目之后, 查看leetcode上的反馈, 查看discussion