文章目录(Table of Contents)
简介
这一部分介绍动态规划的相关内容, 主要从两个例子出发, 来介绍动态规划的主要想法, 和如何使用动态规划来解决实际的问题. 下面四个是动态规划的四个核心点, 可以带着这四个点往下面看例子.
- 递归+记忆化, 我们可以用递归的角度去思考, 接着加上记忆化, 再从初始状态开始考虑, 这样推导出动态规划.
- 定义状态, 这里的状态类似于上面的记忆化, 可以记状态为opt.
- 有状态转移方程, 也叫dp方程, 状态之间转换的关系.
- 存在最优子结构, 因为存在最优子结构, 所以我们才可以把大问题拆分为小的问题解决.
参考资料
Algorithms: Memoization and Dynamic Programming
从斐波那契数列开始
这一部分的截图来自, Algorithms: Memoization and Dynamic Programming.
最简单的递归
我们用斐波那契数列作为例子, 一步一步看一下如何从递归写到动态规划. 我们首先从递归开始, 例如要求fib(6), 那么可以写成要求fib(6)=fib(5)+fib(4), 于是依次这样分解到fib(1).
- def fib_01(n):
- """直接使用递归解决
- """
- # 结束条件
- if n <= 1:
- return n
- # 调用递归
- a = fib_01(n-1) + fib_01(n-2)
- # 进行处理
- return a
但是上面的递归会存在一些问题, 也就是存在很多值进行了重复的计算. 如下图所示, 我们可以看到fib(3)被重复计算了3次.
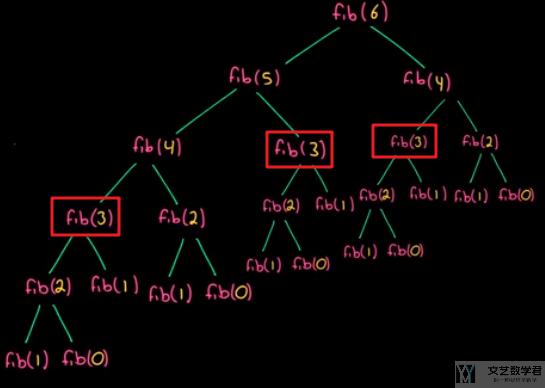
递归加存储
为了解决上面的问题, 我们在递归的过程中加入了存储, 也就是保存计算过的fib的值. 也就是对应下面的memo, 我们用一个字典类型来记录计算过的值. 例如memo[3]就是记录fib(3)的值.
需要注意的是, 在递归调用的时候, memo类似于一个全局变量的感觉. 关于递归函数参数的说明, 可以查看这个链接, python查看内存地址
- def fib_02(n, memo={}, level=0):
- """递归+记忆化(memo记录fib(n)的值)
- """
- # 结束条件
- if n <= 1:
- memo[n] = n
- print('='*level, end='')
- print('> level:{}, n:{}, memo:{}'.format(level, n, memo))
- return memo[n]
- # 调用递归
- if n not in memo:
- memo[n] = fib_02(n-1, level=level+1) + fib_02(n-2, level=level+1)
- # 进行处理
- print('='*level, end='')
- print('> level:{}, n:{}, memo:{}'.format(level, n, memo))
- return memo[n]
加入记忆之后, 整个计算流程变成了下面的样子. 因为我们每次计算都会存储相应的值, 所以就只需要如下图的计算.
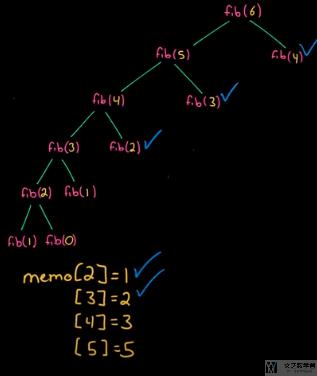
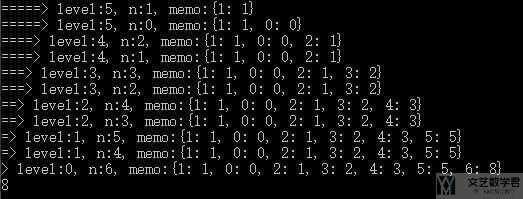
我们看一下实际运算的输出值, 与上面的树状图对应一下. 我们从level=0开始看起.
- 为了计算fib(6), 需要计算fib(5)+fib(4), level=0的内容.
- 接着是fib(5)=fib(4)+fib(3), level=2的内容. 上面level=1中的fib(4)还没开始计算, 要先将左侧的计算完毕. 也就是先从fib(4)继续往下递归. fib(3)会是从下向上返回的时候用到, 那个时候可以直接从memo中进行读取.
- 接着是fib(4)=fib(3)+fib(2), level=3的内容.
- 接着是fib(3)=fib(2)+fib(1), level=4的内容.
- 接着是fib(2)=fib(1)+fib(0), level=5的内容.
动态规划(从初始状态开始写)
有了上面的思路之后, 动态规划就是可以从初始状态向上进行推导. 也就是, 我们的初始状态是fib(0)和fib(1), 接着计算fib(2).
也就是上面的树状图是从下往上进行推导的. 同样在这里也是需要memo的, 需要记录下每一个状态的值. 样例代码如下所示.
- def fib_03(n, memo={0:0, 1:1}):
- """递推(将递归用正序来写)+记忆化(memo记录fib(n)的值)
- """
- # 直接按照dp方程写出式子
- for i in range(2, n+1):
- memo[i] = memo[i-1] + memo[i-2]
- # 进行处理
- return memo[n]
计算路径个数
上面斐波那契数列的dp公式比较好推出, 下面我们看一下一个比较复杂的问题. 计算路径的个数. 如下图所示, 我们要计算从起点(start)开始, 到终点(end), 一共有多少种不同的走法. 其中有红色涂色的地方表示是不可以通行的. 且我们只能向右或是向下行走.
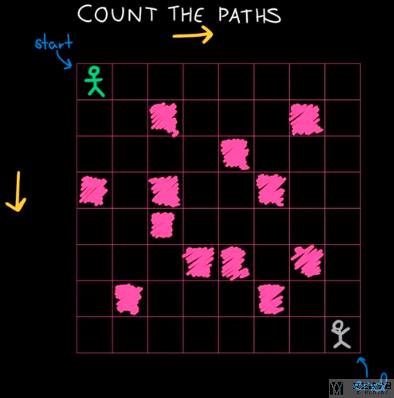
使用递归解决
我们要计算从起点到终点的路径的总的个数, 可以将问题转换为计算从A到终点的路径总和加上B到终点的路径总和.

也就是paths(start, end)=paths(A, end) + paths(B, end). 我们用同样的想法计算paths(A, end)和paths(B, end). 也就是可以用下图进行表示.
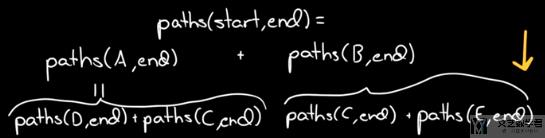
我们直接使用递归来进行解, 代码如下, 还是按照上面的思路, 还是按照结束条件, 递归步骤, 数据处理进行实现.
- def paths(endX, endY, x, y, level=0):
- # 初始化陷阱位置
- traps = ((1,2),(1,6),
- (2,4),
- (3,0),(3,2),(3,5),
- (4,2),
- (5,3),(5,4),(5,6),
- (6,1),(6,5))
- # 结束条件
- if (x==endX-1 and y==endY) or (x==endX and y==endY-1): # 终点
- return 1
- if (x>7) or (y>7): # 边界
- return 0
- if (x,y) in traps: # 陷阱
- return 0
- # 进行的递归
- a = paths(endX, endY, x+1, y, level=level+1) + paths(endX, endY, x, y+1, level=level+1)
- # 处理数据
- return a
递归加存储
同样, 在上面的计算过程中, 有很多的节点是被重复计算的. 例如下图中paths(c, end)就被重复计算了两次.

于是我们在这里加上存储. 来加快速度. 也就是每个点我们知道了路径条数之后, 就存储起来.
- import numpy as np
- def paths(endX, endY, x, y, level=0):
- # 初始化陷阱位置
- traps = ((1,2),(1,6),
- (2,4),
- (3,0),(3,2),(3,5),
- (4,2),
- (5,3),(5,4),(5,6),
- (6,1),(6,5))
- # 结束条件
- if (x==endX-1 and y==endY) or (x==endX and y==endY-1): # 终点
- panel[x,y] = 1
- return 1
- if (x>7) or (y>7): # 边界
- return 0
- if (x,y) in traps: # 陷阱
- panel[x,y] = 0
- return 0
- # 进行的递归
- if panel[x,y] == -1:
- panel[x,y] = paths(endX, endY, x+1, y, level=level+1) + paths(endX, endY, x, y+1, level=level+1)
- print('='*level, end='')
- print('> level:{}, (x:{}, y:{}), Result:{}'.format(level, x, y, panel[x,y]))
- # 处理数据
- return panel[x,y]
- if __name__ == "__main__":
- global panel # 保存整个棋盘, 使用全局变量
- panel=-1*np.ones((8,8))
- print(paths(endX=7, endY=7, x=0, y=0))
- print(panel)
我们在这里为了更加清楚, 使用全局变量panel来进行存储. 于是最后从每个点出发, 到end的路径条数都计算出来了.
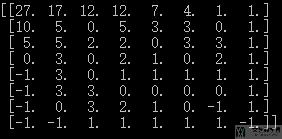
动态规划(从初始状态开始写)
现在我们倒过来想, 从终点开始, 设整个格子用变量panel表示, 为一个8*8的向量.
- 初始状态为panel[7, 7]=1, panel[7, 6]=1, panel[6, 7]=1
- dp方程为:
- panel[i, j] = panel[i+1, j] + panel[i, j+1]
- panel[i, j] = 0, 如果(i, j)是不能走的地方
- panel[i, j] = 0, 如果i>7或是j>7(超出棋盘)
完整的代码如下所示, 注意还是使用了全局变量.
- import numpy as np
- def paths(endX, endY):
- # 初始化陷阱位置
- traps = ((1,2),(1,6),
- (2,4),
- (3,0),(3,2),(3,5),
- (4,2),
- (5,3),(5,4),(5,6),
- (6,1),(6,5))
- # 状态初始化
- starts = ((7,7),(7,6),(6,7))
- panel[7,7] = 1
- panel[7,6] = 1
- panel[6,7] = 1
- # dp方程
- for i in range(endX, -1, -1):
- for j in range(endY, -1, -1):
- if (i, j) in traps:
- panel[i, j] = 0
- elif (i,j) in starts:
- pass
- elif i == endX: # 边界处理
- panel[i, j] = panel[i, j+1]
- elif j == endY: # 边界处理
- panel[i, j] = panel[i+1, j]
- else:
- panel[i, j] = panel[i+1, j] + panel[i, j+1]
- if __name__ == "__main__":
- global panel # 保存整个棋盘, 使用全局变量
- panel=-1*np.ones((8,8))
- print(paths(endX=7, endY=7))
- print(panel)
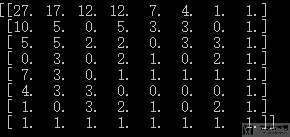
最终的panel的输出结果如下, 需要注意的是, 这里的结果和上面用递推的结果会有些不一样. 例如上面会存在-1, 这是因为存在一些障碍, 导致从起点开始, 有一些节点我们是走不到的, 所以用递推的时候最终结果会存在-1, 不过结果是一样的:
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-






评论