文章目录(Table of Contents)
简介
这里单独介绍一些动态规划的习题. 上一篇我们讲了动态规划的基础内容, 数据结构与算法基础-动态规划, 但是动态规划里面有很多的习题, 还是要多看些习题去了解动态规划. 所以单独拿出一篇来, 来总结一些我见过的动态规划的习题. 这个题目也是不定时往里面更新, 做了新的题目就往里面增加.
爬楼梯问题
这是leetcode上第70题, Climbing Stairs. 这一题的要求就是, 爬一个N级的楼梯, 每次可以走一级或是两级, 一共有多少种不同的走法.
我们可以这样来思考, 如果要上N级的台阶, 我们可以从N-2级上去, 或是从N-1级上去. 于是上N级台阶的总的走法是N-2级与N-1级走法的和.
- 写出dp方程就是: obj(N) = obj(N-1)+obj(N-1). 这个是和斐波那契数列的递推公式是一样的.
- 初始值是, obj(1)=1, obj(2)=2
于是, 我们就根据上面的dp方程写出相应的代码.(这里就不多解释了, 这个就和斐波那契数列是一样的)
- class Solution:
- def climbStairs(self, n: int) -> int:
- obj = {1:1, 2:2}
- for i in range(3, n+1):
- obj[i] = obj[i-1] + obj[i-2]
- return obj[n]
三角形最短路径和
这是leetcode上第120题, Triangle. 题目要求是, 计算从三角形最顶端到三角形底端的最小路径和. 且移动的时候只能移动到相邻的点. 例如下面的这个例子, 5只能移动到1和8.
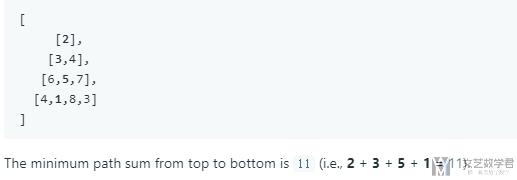
这一题还是使用动态规划来进行解决. 关于使用动态规划来进行问题的解决, 还是分为两个步骤: 1. 状态的定义; 2. dp方程的定义.
- 这里, 状态obj[i,j]定义为从(i,j)这个点到末尾的最短路径. (注意是从这个点出发, 到底部的最短路径)
- dp方程为, obj[i, j] = min(obj[i+1, j], obj[i+1, j+1]) + triangle[i, j]
- 初始状态为所有三角形的底部元素.
于是, 我们按照上面的思路可以写出下面的代码.
- class Solution:
- def minimumTotal(self, triangle: List[List[int]]) -> int:
- # 初始条件
- lenT = len(triangle) # 三角的层数
- obj = {}
- for index, value in enumerate(triangle[-1]):
- obj[(lenT-1,index)] = value
- # dp方程
- for i in range(lenT-2, -1, -1): # 层
- for index, value in enumerate(triangle[i]): # 每一层元素
- obj[(i,index)] = min(obj[(i+1,index)], obj[(i+1,index+1)]) + value
- return(obj[(0,0)])
这里和贪心的区别是, 不是只看当前的最小值, 而是看从当前到底部的最小值. 对未来有一个预见性.
代码优化版本(逻辑没上面清楚)
上面的代码是比较容易理解的版本, 我们可以进一步缩小存储空间, 不使用二维数组去保存, 使用一维数组进行保存, 每次只保存上一层的所有值(这个没有上一个版本逻辑清楚).
- class Solution:
- def minimumTotal(self, triangle: List[List[int]]) -> int:
- # 初始条件
- lenT = len(triangle)
- obj = triangle[-1]
- # dp方程
- for i in range(lenT-2, -1, -1): # 层
- print('obj:{}'.format(obj))
- for index, value in enumerate(triangle[i]): # 每一层元素
- obj[index] = min(obj[index], obj[index+1])+value
- return(obj[0])
- if __name__ == "__main__":
- sol = Solution()
- tr = [[2],[3,4],[6,5,7],[4,1,8,3]]
- print(sol.minimumTotal(triangle=tr))
这里关键是在两层循环里面那行语句, 我们每次都使用obj这个一维数组. 因为是三角形, 后面的行的元素一定比上面的多, 所以我们每次将新的行的元素对应的值保存在这个数组里面.
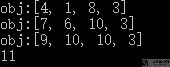
我们看一下这里obj的变化. 第一次打印, 我们将三角形最底端的值保存进去, 也就是[4, 1, 8, 3]. 接着对上一行进行处理, 第二行的第一个值的计算方式, 7=min(4, 1)+6, 对应上面的dp方程.
在最后一轮, 因为第二层只有两个数, 所以数组的第一个元素=min(9, 10)+2, 所以我们返回obj[0]即可.
这里就是一个额外的介绍, 正常我们还是可以使用二位数组来进行计算, 思路会更加清楚一些.
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-






评论