数据结构与算法基础-递归与分治

王 茂南
王 茂南
王 茂南
2825
文章
75
评论
2020年4月17日07:25:58
评论 2342字阅读7分48秒
摘要这一篇介绍关于算法的内容, 递归和分治的介绍. 会有递归和分治基础的介绍和相关的示例题目.

简介

这一篇介绍递归(recursion)与分治(divde and conquer). 会首先介绍递归(recursion)与分治(divide)的基础知识, 后面介绍几个leetcode上可以使用递归思想解决的问题.

 

基础知识-递归

递归就是函数自己调用自己. 用一个比较经典的电影<盗梦空间>来说明就是:

  • 我们可以从一个梦境进入下一个梦境, 直到进入最后一个(递归的结束条件);
  • 接着我们从最后一个梦境向前面的梦境返回, 返回的时候通常会对从上一个梦境带来的内容进行操作(递归的时候的数据处理, 所以数据处理的步骤要写在函数调用自己的后面).
  • 最后就是走出梦境(结束递归)

总的过程如下图所示, 先下到最后的梦境, 再逐层返回, 返回的过程中对数据处理.

数据结构与算法基础-递归与分治

下面来看递归的例子, 详细看代码部分的结构.

 

递归的例子-阶乘的计算

我们用阶乘来详细说明一下递归. 并说明一下写递归程序的时候程序大致的结构. 阶乘写成递归的式子如下所示.

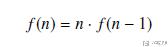
数据结构与算法基础-递归与分治

且递归的结束条件是, n=1的时候, 返回1. 于是, 整体的代码可以写成下面这个样子. 一般在写递归的时候, 我们在函数里面定义一个level, 查看一下在递归的哪一层.

  1. def Factorial(n, level=0):
  2.     # 递归结束条件
  3.     if n <= 1:
  4.         print('='*level, end='')
  5.         print('> level:{}, n:{}, result:{}'.format(level, 1, 1))
  6.         return 1
  8.     # 递归(调用自己)
  9.     a = Factorial(n-1, level=level+1)
  11.     # 完成上面递归之后执行的操作
  12.     a = n*a
  13.     print('='*level, end='')
  14.     print('> level:{}, n:{}, result:{}'.format(level, n, a))
  15.     return a
  17. if __name__ == "__main__":
  18.     print(Factorial(6))

上面整体代码分为三个部分, 分别是:

  • 递归结束条件
  • 递归(调用自身)
  • 完成上面递归之后执行的操作.

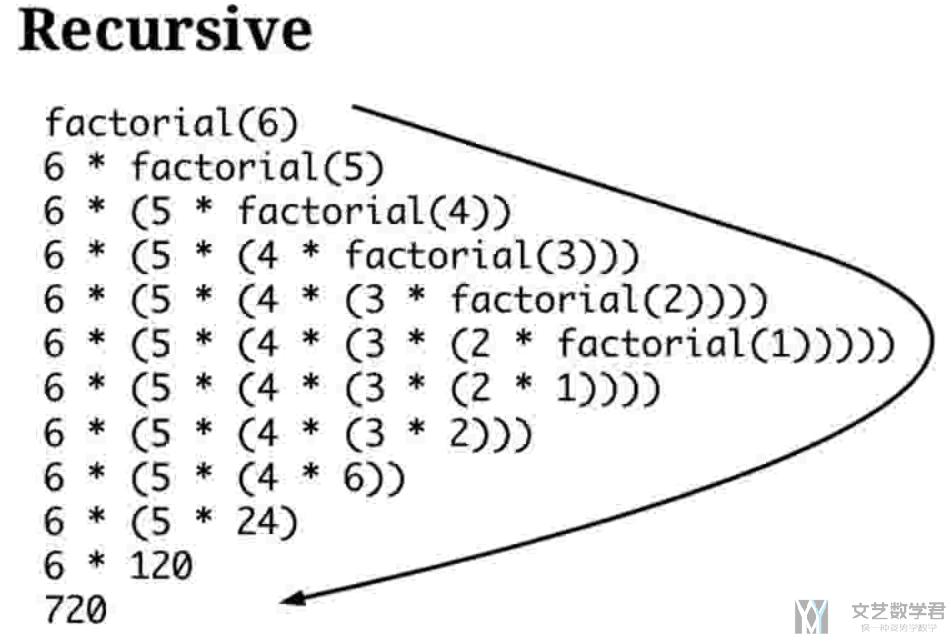
于是上面的输出结果如下所示, 最先输出的是最后一层, 也就是level=5的地方(梦境的最下面), 接着逐层返回, 返回的时候将返回的结果乘上n返回到上一层.

例如在下面的图中, level=3中, 返回的值是level=4的result=2乘上level=3的n=3, 于是将6返回给level=2的层级.

数据结构与算法基础-递归与分治

这里总体的流程如下图所示, 逐层展开, 到最底层, 再逐层向上:

数据结构与算法基础-递归与分治

 

 

基础知识-分治

分治就是divde and conquer. 也就是将一个大问题划分为小问题, 再对小问题一一进行解决. 分治在计算的时候, 需要中间没有很多重复变量. 像计算斐波那契数列, 中间会有重复的值用到多次, 直接使用分治的方法就不会很快, 我们可以选择将中间的量进行存储.

 

分治的例子-计算n次方

接下来看一个leetcode上第50题, powx n. 这里需要计算x^n, 也就是计算pow(x,n). 比如说2^10=1024. 如果直接使用循环来解决这个问题, 世家你复杂度是O(n).

我们用分治(递归)的方法来解决这个问题. 我们首先写出总体的思路.

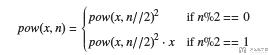
数据结构与算法基础-递归与分治

例如2^7就是2^7=(2^3)(2^3)2. 也就是对应上面n为基数的情况. 这时候, 时间复杂度为O(logN). 下面看一下具体的代码.

  1. class Solution(object):
  2.     def showTrace(self, level, n, a):
  3.         """打印递归过程函数
  4.         """
  5.         print('='*level, end='')
  6.         print('> level:{}, 2^n, n:{}, Result:{}'.format(level, n, a))
  9.     def myPow(self, x: float, n: int, level=0) -> float:
  10.         # 终止条件
  11.         if n == 0:
  12.             self.showTrace(level, n, a=1)
  13.             return 1
  14.         elif n == -1:
  15.             self.showTrace(level, n, a=1/x)
  16.             return 1/x
  18.         # 调用递归
  19.         a = self.myPow(x=x, n=n//2, level=level+1)
  21.         # 进行处理
  22.         if n % 2 == 0:
  23.             a = a * a
  24.             self.showTrace(level, n, a=a)
  25.         elif n % 2 == 1:
  26.             a = a * a * x
  27.             self.showTrace(level, n, a=a)
  28.         return a
  30. if __name__ == "__main__":
  31.     sol = Solution()
  32.     sol.myPow(x=2, n=17)

最终的结果如下所示:

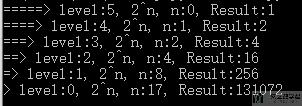
数据结构与算法基础-递归与分治

可以看到, 为了计算2^17:

  • 首先拆分为(2^8)*(2^8)*2.
  • 接着计算2^8, 拆分为(2^4)*(2^4)
  • 接着计算2^4, 拆分为(2^2)*(2^2)
  • 接着计算2^2, 拆分为(2^1)*(2^1)
  • 接着计算2^1, 拆分为(2^0)*(2^0)*2.
  • 有了2^1, 就可以逐层向上倒推了.

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2020年4月17日07:25:58
  • 转载请务必保留本文链接：https://mathpretty.com/12162.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: