最优停止与选择心仪对象

简介

在生活中，我们经常面临需要在不完全信息下做出决策的情形。从挑选伴侣、购买房产到职业选择，如何在恰当的时刻做出最佳选择是一个普遍而复杂的问题。

本文将介绍数学中的「最优停止问题」，会描述这个问题，并探讨如何应用这一理论来优化决策过程，增加成功的概率。这个问题其实也就是：你将要穿过一片麦田，在不能回头的前提下，如何摘下一株最大的麦穗？下面是这个问题的结论：

对于这类最优停止问题，可以采取的措施为：先拒绝前面的一定比例的候选人（或是事），用来观察和建立一个「标准」，然后从剩下的中选择第一个比之前所有候选人都好的人。这里比例通常为 37%，也就是接近 1/3。

参考资料

• 死理性派恋爱法：拒绝掉前面37%的人；
• 如何选择心仪对象，非常有意思的博客；
• 男生追女生的数学模型，非常有意思的论文；
• 最优停止理论——如何适“可”而止，部分的推导是从这里借鉴的，进行了一些完善；

问题描述

最优停止问题介绍

最优停止问题是决策理论中的一个经典问题，它涉及在一系列选择中决定最佳停止点的问题。这类问题的特点是：选项是顺序出现的，一旦放弃了某个选项，就无法再回头选择。同时我们也不清楚未来会遇到什么样子的方案，即未来是不可知的。因此，决策者必须在没有完全信息的情况下，基于已有的观察来做出最佳选择。

最优停止问题例子

一个广为人知的最优停止问题是「秘书问题」，或是被称为「相亲问题」，「苏丹的嫁妆问题」。这个问题假设是：你需要聘请一名秘书，有多个候选人按随机顺序进行面试。你在每次面试后都必须决定是否聘用当前的候选人。如果拒绝了，就不能再回头选择他。问题的关键在于找到一种策略，使得选择最佳候选人的概率最大化。

面对这类问题，Merrill M. Flood 在1949年首次提出 37% 法则。他所采取的的策略为：

1. 首先对前面一部分面试者，无论优秀与否都直接拒绝，只考察目标，收集数据，用于确定「最基本的满意标准」。
2. 然后对剩下的人进行面试，如果遇到一位比之前面试的人都优秀的面试者，那么就立即出手，直接聘请这个人，否则就继续面试

通过计算，Flood发现 37% 是一个最优停止点，也就是说选择前37%的人直接拒绝时，得到最适合担任秘书的人的概率最大。下面我们分享一下 37% 是如何计算得到的。

数学描述

问题描述

假设有 n 那个候选人，他们的质量顺序是随机的。你需要在面试过程中决定是否雇佣当前的候选人。一旦你拒绝了一个候选人，就不能再回头选择他。问题是确定一个策略，使得选择最优候选人的概率最大化。

策略选择

最优策略是：先拒绝前面的一定比例的候选人，用来观察和建立一个「标准」，然后从剩下的候选人中选择第一个比之前所有候选人都好的人。问题的关键是确定应该拒绝前面多少个候选人。

确定最优拒绝比例

下面开始推导最优的拒绝比例。首先我们定义变量：

• n：候选人总数。
• r：观察的候选人数，这些候选人只用于设定标准，不会被选择。
• k：表示第 k 个人是最优的候选人。

现在我们假设有两个事件，事件 A_k 表示第 k 个人被选中，事件 B_k 表示第 k 个人是最优秀的。于是我们希望最大化 k 取不同数值时候，P(A_k, B_k) 的概率，也就是：

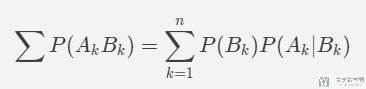
对于 P(B_k)，表示第 k 个人是最优秀的，概率是 1/n，这个会随机出现 n 个候选人中的一个。此时上面的式子可以化简为如下的式子，我们将求和拆开：

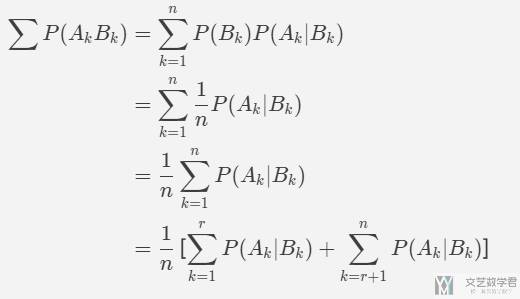
这里 P(A_k|B_k) 表示第 k 个人被选中的概率。由于我们的策略是：

• 当 k<=r 的时候，我们不会进行任何选择，因此此时 P(A_k|B_k)=0；
• 对于 k>r 的时候，若选择第 k 个人，则表示在 r+1~k-1 里面，没有比 k 更好的人。或者可以说 0~k-1 之间的最大值，出现在 0~r 之间，此时的概率为 r/(k-1)。

于是上面的式子可以进一步化简，变为：

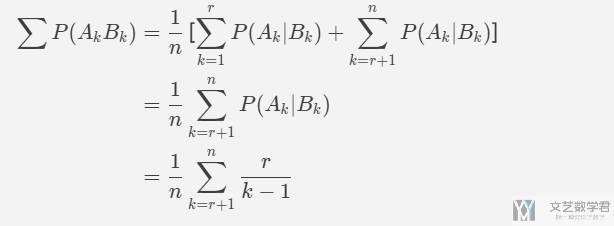
我们希望上面的概率最大，于是将其转换为积分的形式：

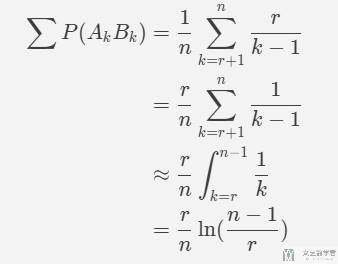
对于上面的积分运算，可以参考下面是式子：

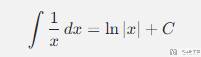
为了求上面式子最大，我们对其进行求导，也就是

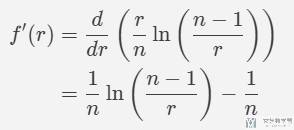
我们使得导数为 0，对上面式子求解，得到 r=(n-1)/e，也就是差不多总人数 37% 左右。

仿真实验

接下来我们进行仿真实验。首先测试选择比例都接近 0.37 的时候，此时选择是最优的概率如下表所示。可以看到选中最优的概率是接近 0.37 的。

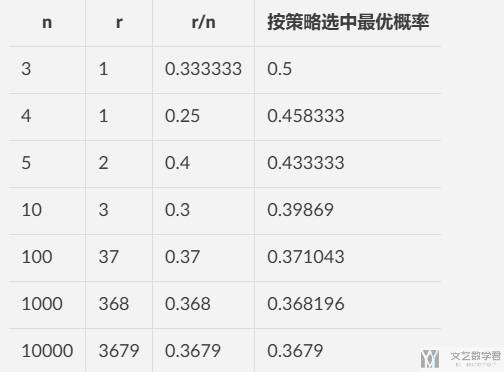
接下来我们测试不同的拒绝比例（也就是不同的 r/n）对结果的影响。结果如下图所示，可以看到在接近 0.35-0.45 之间的时候，按策略可以选中最优的概率是最大的：

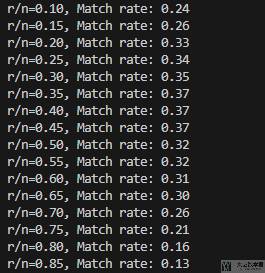
下面是对于的代码，大家可以尝试不同的参数来验证结果：

当然，上面讲了这么多，只是为了解决一个最优化的问题。很多时候，比如谈恋爱（可能我们是有先验条件的），那这个结论不再成立（所以，也不要对照着这个来谈恋爱），如果一开始就很合适，也是可以在一起的。

最后在生活中，我们需要灵活的应用37%法则，结合自己的经验，寻找到那个令人满意的「可」之所在。