优化均方根误差检验的预测问题

这一篇也是自己在整理文件的时候发现的，是一次在参加数据挖掘比赛的时候看到的。大概内容是关于需要预测一组数据，有三次提交的机会，使用均方根误差来做检验预测是否正确。

在这种情况下，我们除了在改进模型的，还有什么办法可以使得预测得更加精确呢，下面就提供了一种方法。

我还是直接使用手写的公式推导来完成相关的介绍。（感觉这次字写得好丑呀）

下面截一下当时ppt上的图片，帮助理解：

对于上面的公式，我们使用python来实现以下：

我们看一下运行的结果：

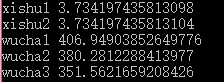
对于上面的打印结果，我们分析以下：

• xishu1是真实的优化系数，是拿真实值计算的，实际情况我们是算不出的；
• xishu2是我们通过上面的方法计算得到的，可以看到与真实的相差不大
• wucha1，wucha2分别是前两次预测的误差
• wucha3是我们优化后的预测值的误差，可以看到比前面两个都小，可以看到是有效果的

以上就是关于优化均方根误差检验的预测问题，希望以后自己在遇到这种问题可以使用到这种优化的方法（其实实际使用下来，误差不会减小这么多，但是也是会减小的，在无法优化模型的情况下，可以使用这种方法进行优化）。