Mathematica散点图美化

散点图是我们在可视化里经常会使用的一种图形，这一篇文章会讲一下一种关于散点图的美化方式，增加颜色和大小。（这里不使用ListPlot进行绘制，而是使用了另外的一个方法）

同时，如果我们把颜色和大小也看成两个维度的话，我们就可以使用二维的散点图画出有四个维度的数据来，还是很方便的。

增加散点的色彩

我们首先增加散点图的颜色，颜色是可以用来分类的。如有三种不同类型的产品的散点图，我们就可以用三种颜色来表示，我们看一下下面的实现方法：

(*pts中的数据类似{名字,横座标,纵座标,大小,随机数(用来控制最后的颜色)}*)
pts = Table[{"Name" <> ToString[i], RandomReal[20], RandomReal[20],  17, RandomReal[]}, {i, 100}];
(*画出圆盘的位置和对应的大小*)
fp[{name_, x_, y_, size_, c_}] := Style[Disk[{x, y}, Sqrt[size]/10], Hue[c]];
(*对pts中每个数据做fp函数的作用*)
Graphics[fp /@ pts, Axes -> True, AxesOrigin -> {0, 0}]

所以的注释都已经写在代码中了，运行上面的代码，可以得到如下的图：

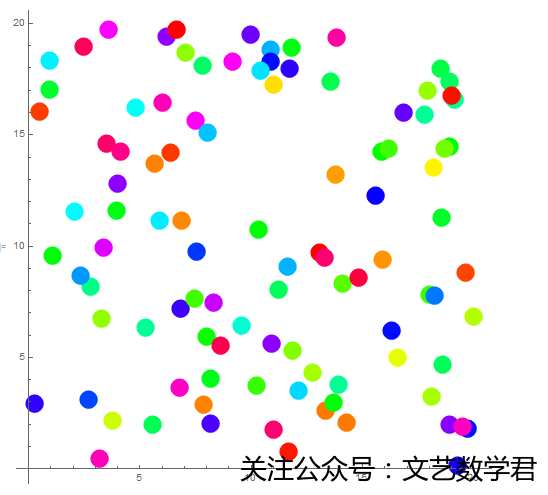
上面这个颜色是随机的，下面看一下我们在实际中可能会遇到的情况：

(*pts中的数据类似{名字,横座标,纵座标,大小,随机数(用来控制最后的颜色)}*)
pts1 = Table[{"Name" <> ToString[i], RandomReal[20], RandomReal[20], 17, .3}, {i, 30}];
pts2 = Table[{"Name" <> ToString[i], RandomReal[20], RandomReal[20], 17, .5}, {i, 30}];
pts3 = Table[{"Name" <> ToString[i], RandomReal[20], RandomReal[20], 17, .7}, {i, 30}];
(*画出圆盘的位置和对应的大小*)
fp[{name_, x_, y_, size_, c_}] := Style[Disk[{x, y}, Sqrt[size]/10], Hue[c]];
(*对pts中每个数据做fp函数的作用*)
Graphics[fp /@ (Flatten[{pts1, pts2, pts3}, 1]), Axes -> True,  AxesOrigin -> {0, 0}]

上面的pts1,pts2,pts3就代表三种数据，然后我们就可以使用颜色来区分三种数据，可以得到下面的图：

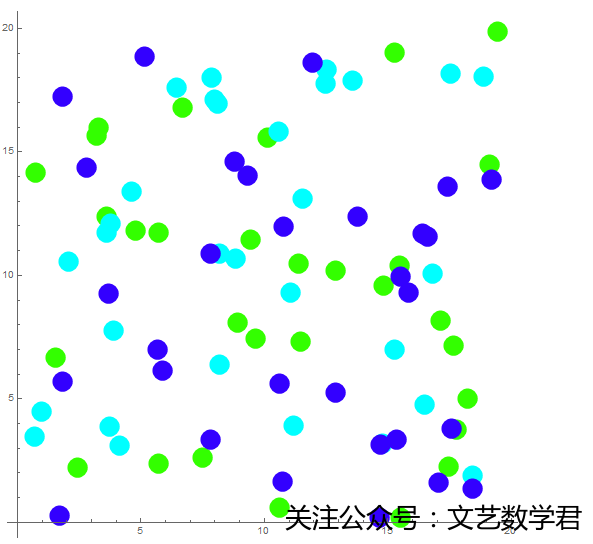
关于修改颜色就到这里，下面看一下如何修改大小。

增加散点的大小

下面我们看一下如何修改散点的大小，其实上面的代码注释上已经写得很明白了，下面还是直接看代码：

(*pts中的数据类似{名字,横座标,纵座标,大小,随机数(用来控制最后的颜色)}*)
pts = Table[{"Name" <> ToString[i], RandomReal[20], RandomReal[20],  RandomInteger[50], RandomReal[]}, {i, 100}];
(*画出圆盘的位置和对应的大小*)
fp[{name_, x_, y_, size_, c_}] :=  Style[Disk[{x, y}, Sqrt[size]/10], Hue[c]];
(*对pts中每个数据做fp函数的作用*)
Graphics[fp /@ pts, Axes -> True, AxesOrigin -> {0, 0}]

在这一副图中我们随机了点的大小和颜色。

最后我们来看一下颜色固定，来修改大小的情况：

(*pts中的数据类似{名字,横座标,纵座标,大小,随机数(用来控制最后的颜色)}*)
pts1 = Table[{"Name" <> ToString[i], RandomReal[20], RandomReal[20],  RandomReal[20], .3}, {i, 30}];
pts2 = Table[{"Name" <> ToString[i], RandomReal[20], RandomReal[20],  RandomReal[{10, 30}], .5}, {i, 30}];
pts3 = Table[{"Name" <> ToString[i], RandomReal[20], RandomReal[20],  RandomReal[{20, 40}], .7}, {i, 30}];
(*画出圆盘的位置和对应的大小*)
fp[{name_, x_, y_, size_, c_}] :=   Style[Disk[{x, y}, Sqrt[size]/10], Hue[c]];
(*对pts中每个数据做fp函数的作用*)
Graphics[fp /@ (Flatten[{pts1, pts2, pts3}, 1]), Axes -> True,  AxesOrigin -> {0, 0}]

于是就能得到下面的这幅图：

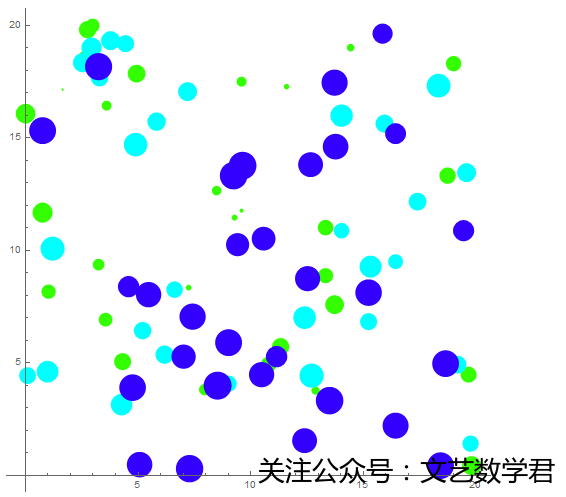
到这里，我们就能灵活对散点图进行灵活的绘制了。