文章目录(Table of Contents)
前言
好久没有使用mathematica了,今天正好看到一个求圆相交情况下阴影的面积的问题(然后没有能够手算出来是多少),就想使用mathematica来计算一下结果,算完之后正好把其他的几种情况也都算了一下,放在这里。
好久没用mathematica,发现还是一样好用。
问题合集
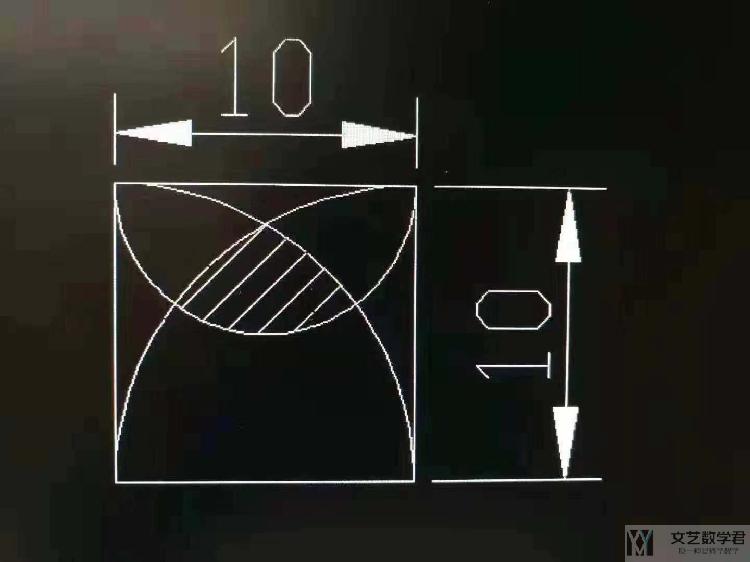
问题一:三圆相交,求阴影面积
要求下图的阴影面积,我尝试了好几次没试出来,<( )>,就用mathematica来计算了。
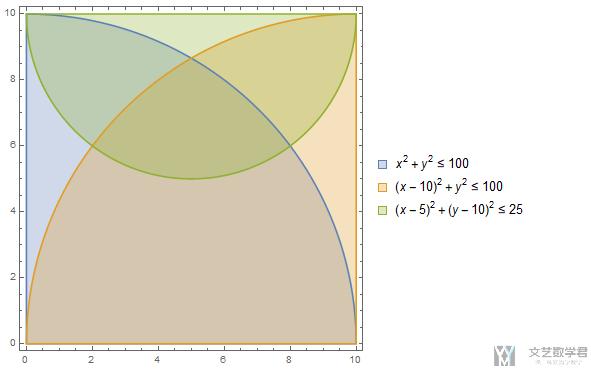
我们首先先把图像画出来看一下:
- RegionPlot[{x^2 + y^2 <= 100, (x - 10)^2 + y^2 <= 100, (x - 5)^2 + (y - 10)^2 <= 25}, {x, 0, 10}, {y, 0, 10}, PlotLegends -> "Expressions"]
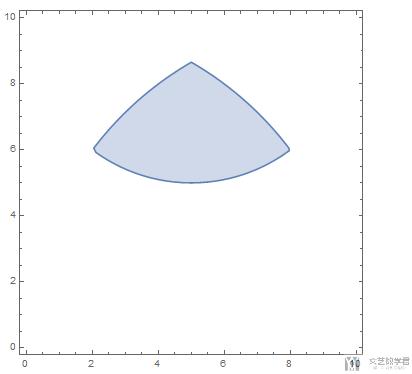
我们再把阴影部分的形状画出来:
- RegionPlot[{x^2 + y^2 <= 100 && (x - 10)^2 + y^2 <= 100 && (x - 5)^2 + (y - 10)^2 <= 25}, {x, 0, 10}, {y, 0, 10}]
下面我们来计算该阴影部分的面积,我们直接使用积分进行计算:
- res = Integrate[Boole[x^2 + y^2 <= 100 && (x - 10)^2 + y^2 <= 100 && (x - 5)^2 + (y - 10)^2 <= 25], {x, 0, 10}, {y, 0, 10}]

上面图片压缩了有点看不清,这里再说一下,解析解是:
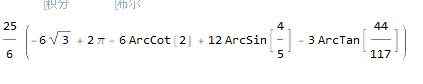
到这里把第一个的阴影部分面积计算完毕了,大家如果有知道如何手算出解析解的,可以在下面留言。
问题二:三圆两两相交圆心,求阴影面积
这是第二个问题,求下面三个圆相交部分的阴影面积:
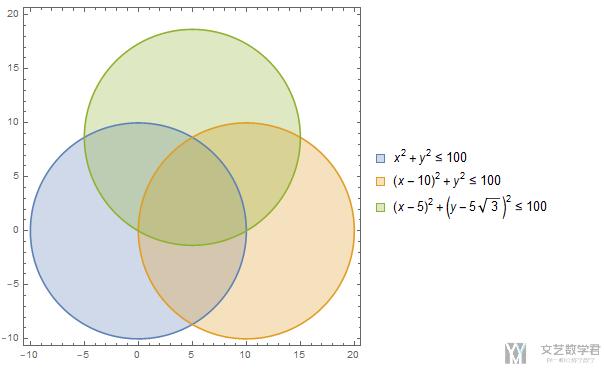
求面积的方法还是和上面一样的方法,就不详细的截图了,看一下阴影部分的形状:
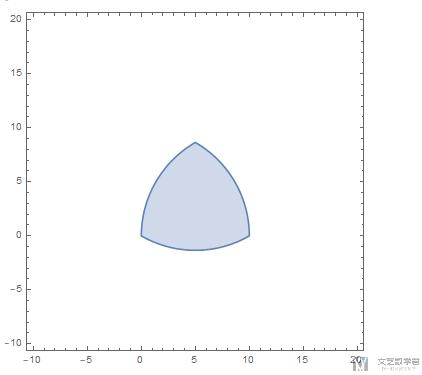
下面就直接求阴影部分的面积:
- res = Integrate[Boole[x^2 + y^2 <= 100 && (x - 10)^2 + y^2 <= 100 && (x - 5)^2 + (y - 5 Sqrt[3])^2 <= 100], {x, -10, 20}, {y, -10, 20}]
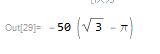
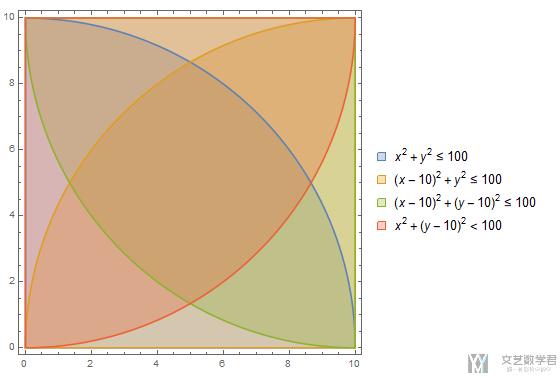
问题三:四圆相交,求阴影面积
跟上面都是一样的步骤,这里就更加简略一些了,首先画出图像:
- RegionPlot[{x^2 + y^2 <= 100, (x - 10)^2 + y^2 <=100, (x - 10)^2 + (y - 10)^2 <= 100, x^2 + (y - 10)^2 < 100}, {x, 0, 10}, {y, 0, 10}, PlotLegends -> "Expressions"]
接着画出相交部分的面积:
- RegionPlot[{x^2 + y^2 <= 100 && (x - 10)^2 + y^2 <=100 && (x - 10)^2 + (y - 10)^2 <= 100 && x^2 + (y - 10)^2 < 100}, {x, 0, 10}, {y, 0, 10}]
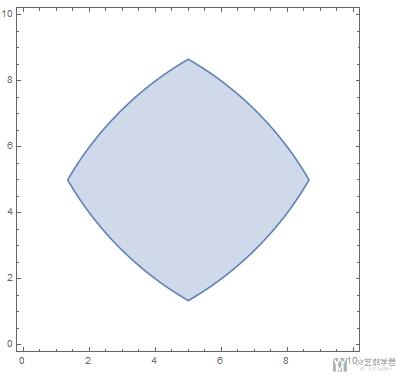
最后求出上面这部分的面积:
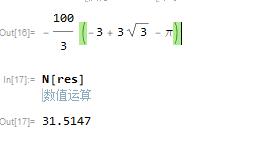
- res = Integrate[Boole[x^2 + y^2 <= 100 && (x - 10)^2 + y^2 <= 100 && (x - 10)^2 + (y - 10)^2 <= 100 && x^2 + (y - 10)^2 < 100], {x, 0, 10}, {y, 0, 10}]
结语
怎么说呢,其实写这一篇文章就是想写写关于mathematica的东西吧,好久没有写了吗,以前有一段时间特别喜欢用,现在开始用的越来越少了。
不知道怎么说,真的很神奇。总之就记录下来吧。
有一篇类似的文章,是求圆柱与球相交的体积的,与这个类似,我把链接放在这里:
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-













评论