Mathematica制作傅里叶变换动图

这是一段在百度贴吧里看到的代码，最后作出的动画效果很有意思，记录在此。

FourierF[a_, t_] := a.Table[Sin[2 Pi i t], {i, Length[a]}]; 
FourierAnim[a_, t_] := Module[{A = Accumulate[a*Table[Cos[2 Pi i t], {i, Length[a]}]],  B = Accumulate[a*Table[Sin[2 Pi i t], {i, Length[a]}]]},  PrependTo[A, 0];
 PrependTo[B, 0];
  Show[Graphics[ Table[{Circle[{A[[i]], B[[i]]}, a[[i]]], Darker[Red],  If[i != Length@a,     Line[{{A[[i]], B[[i]]}, {A[[i + 1]], B[[i + 1]]}}], {Red,    Dashed, Line[{{A[[i]], B[[i]]}, {2, B[[i]]}}]}]}, {i,    Length@a}], PlotRange -> {{-1.5, 3}, {-1, 1}}],  Plot[FourierF[a[[;; -2]], t - \[Tau]], {\[Tau], 2, 3}]]]; 
 a = Table[(1 - (-1)^i)/i, {i, 16}]/Pi;
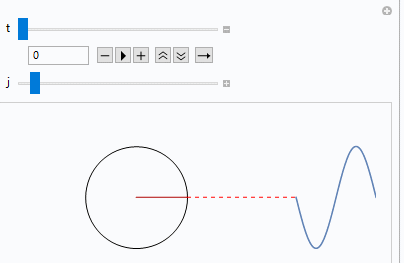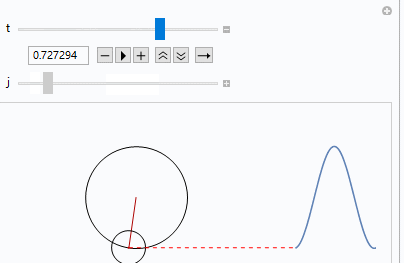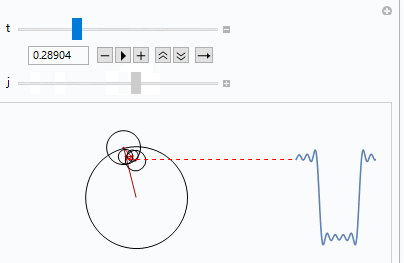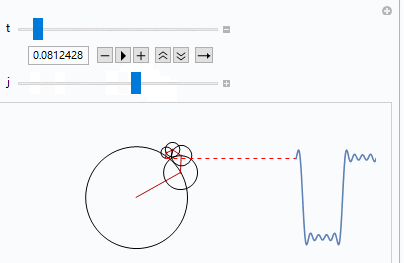
Manipulate[FourierAnim[a[[;; j]], t], {t, 0, 1}, {j, 1, Length@a, 1}]

上面的代码运行出的效果如下：

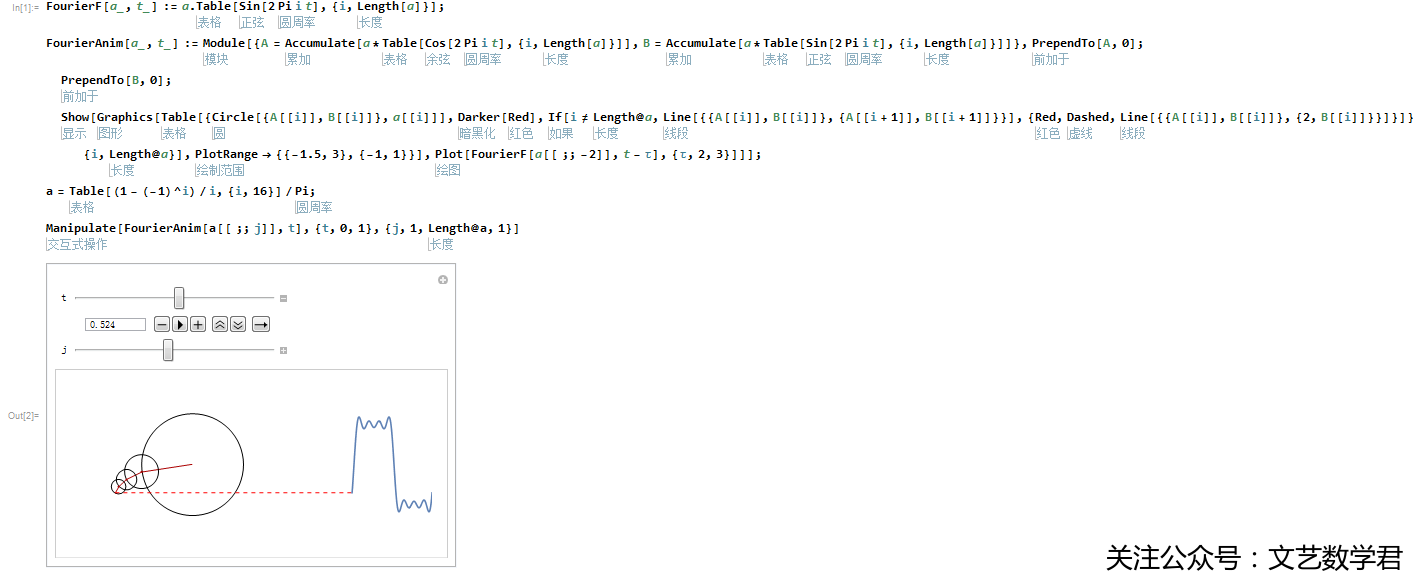
这个图有点小，我们再放大看一下

最后我们来看一下动图