文章目录(Table of Contents)
介绍
阿基米德螺线,也称等速螺线,得名于公元前三世纪希腊数学家阿基米德。阿基米德螺线是一个点匀速离开一个固定点的同时又以固定的角速度绕该固定点转动而产生的轨迹。阿基米德在其著作《螺旋线》中对此作了描述。
数学表达式
阿基米德螺线的极坐标方程式为:
![]()
其中 a 和 b 均为实数。当 ![]()
时,a为起点到极坐标原点的距离。
![]()
b为螺旋线旋转的角速度。改变参数 a相当于旋转螺线,而参数 b 则控制相邻两条曲线之间的距离。
相关自然界现象
自然界中,在千姿百态的生命体上发现了不少螺旋。如原生动物门中的砂盘虫;软体动物门中梯螺科中的尖高旋螺,凤螺科中的沟纹笛螺,明螺科中的明螺,又如塔螺科的爪哇拟塔螺、奇异宽肩螺、笋螺科的拟笋螺等大多数螺类,它们的外壳曲线都呈现出各种螺旋状;在植物中,则有紫藤、茑萝、牵牛花等缠绕的茎形成的曲线,烟草螺旋状排列的叶片,丝瓜、葫芦的触须,向日葵籽在盘中排列形成的曲线;甚至构成生命的主要物质——蛋白质、核酸及多糖等生物大分子也都存在螺旋结构,如人类遗传基因(DNA)中的双螺旋结构。其中,自然界中的砂盘虫化石,蛇盘绕起来形成的曲线等都可以构成阿基米德螺线。
螺线之所以在生命体中广泛存在,是由于螺线的若干优良性质所确定。而这些优良性质直接或间接地使生命体在生存斗争中获得最佳效果。

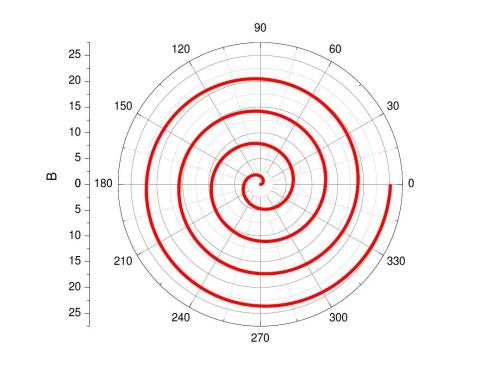
绘制介绍
这里为了显示的效果,直接将图片截图在这里。
参考链接
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-











评论