Python科学运算–简单汇总

王 茂南
王 茂南
王 茂南
3132
文章
75
评论
2019年3月30日20:40:58
评论1 4386字阅读14分37秒
摘要这一篇会简单记录一下在Python中进行科学运算的方式, 也是方便自己之后的使用.

前言

这一篇记录一下关于Python在科学运算上的一些操作，方便查询。之后会不定期补充。

矩阵运算

  1. import numpy as np
  2. x_test = np.array([[1,2,3],[3,4,6],[4,7,11]])
  3. print(x_test)
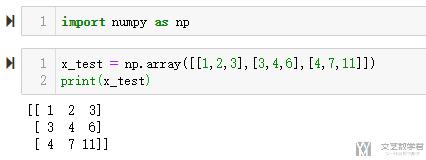
Python科学运算–简单汇总

矩阵转置

  1. # 求矩阵转置
  2. np.transpose(x_test)
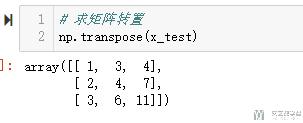
Python科学运算–简单汇总

当然，也可以通过下面方式求转置

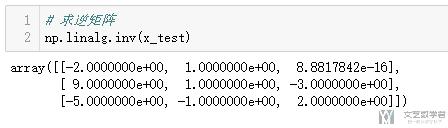
Python科学运算–简单汇总

矩阵求逆

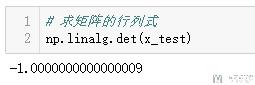
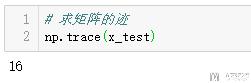
Python科学运算–简单汇总

矩阵求行列式

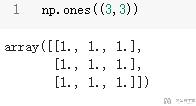
Python科学运算–简单汇总

矩阵求迹

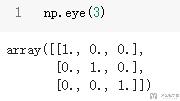
Python科学运算–简单汇总

生成全1矩阵

Python科学运算–简单汇总

生成对角矩阵

Python科学运算–简单汇总

特征值与特征向量

  1. # 求矩阵的特征值与特征向量
  2. w, v = np.linalg.eig(x_test)
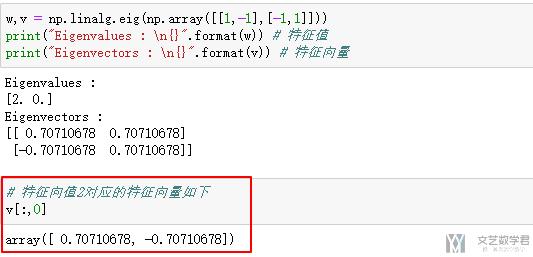
  3. print("Eigenvalues : \n{}".format(w)) # 特征值
  4. print("Eigenvectors : \n{}".format(v)) # 特征向量
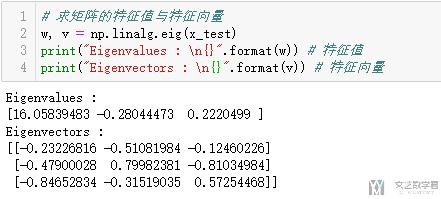
Python科学运算–简单汇总

特别要注意的是，特征值w[i]对应的特征向量为v[:,i]，我们看一下下面的例子：

Python科学运算–简单汇总

SVD分解

  1. x_test = np.array([[1,2],[3,4],[5,6]])
  2. # 进行svd分解
  3. u,e,v = np.linalg.svd(x_test)
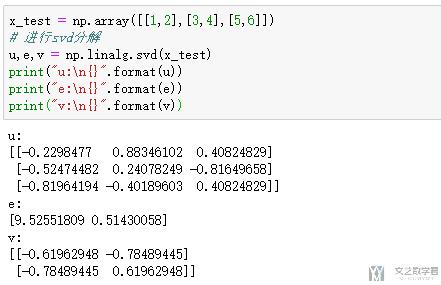
  4. print("u:\n{}".format(u))
  5. print("e:\n{}".format(e))
  6. print("v:\n{}".format(v))
Python科学运算–简单汇总
  1. # 将e矩阵补齐
  2. e_n = np.zeros([3,2])
  3. for i in range(2):
  4.     e_n[i][i] = e[i]
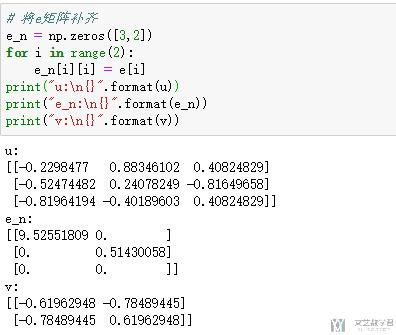
  5. print("u:\n{}".format(u))
  6. print("e_n:\n{}".format(e_n))
  7. print("v:\n{}".format(v))
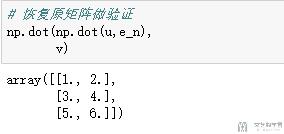
Python科学运算–简单汇总

下面验证一下SVD分解的结果是否正确

  1. # 恢复原矩阵做验证
  2. np.dot(np.dot(u,e_n),
  3.        v)
Python科学运算–简单汇总

矩阵乘法

  1. x_test = np.array([[1,2,3],[4,5,6]])
  2. np.dot(x_test, x_test.T) # 2*3 3*2
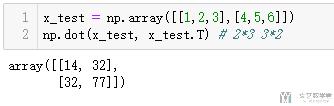
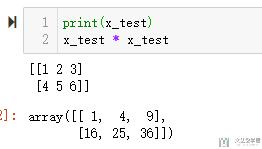
Python科学运算–简单汇总

若直接使用乘法, 只是元素间的两两相乘;

Python科学运算–简单汇总

统计相关

均值, 方差, 标准差

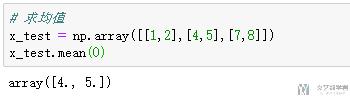
  1. # 求均值
  2. x_test = np.array([[1,2],[4,5],[7,8]])
  3. x_test.mean(0)
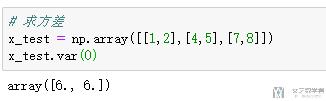
Python科学运算–简单汇总
  1. # 求方差
  2. x_test = np.array([[1,2],[4,5],[7,8]])
  3. x_test.var(0)
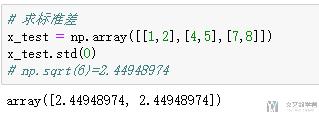
Python科学运算–简单汇总
  1. # 求标准差
  2. x_test = np.array([[1,2],[4,5],[7,8]])
  3. x_test.std(0)
  4. # np.sqrt(6)=2.44948974
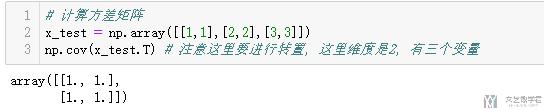
Python科学运算–简单汇总

协方差矩阵

  1. # 计算方差矩阵
  2. x_test = np.array([[1,1],[2,2],[3,3]])
  3. np.cov(x_test.T) # 注意这里要进行转置, 这里维度是2, 有三个变量
Python科学运算–简单汇总

相关系数矩阵

  1. x_test = np.random.randint(2,10,(100,3)) # 随机生成一组数据
  2. pd.DataFrame(x_test).corr() # 相关系数矩阵
Python科学运算–简单汇总

 

协方差矩阵与相关系数矩阵可视化

有时候，我们会把相关系数矩阵绘制成heatmap，这样可以更加直观的显示出效果；

  1. import seaborn as sns
  2. import matplotlib.pyplot as plt
  3. %matplotlib inline
  5. # 这里数据集是我之前的一个数据, 具体使用的时候进行修改即可
  6. dfData = data_guess.iloc[:,:7].cov()
  7. plt.subplots(figsize=(9, 9)) # 设置画面大小
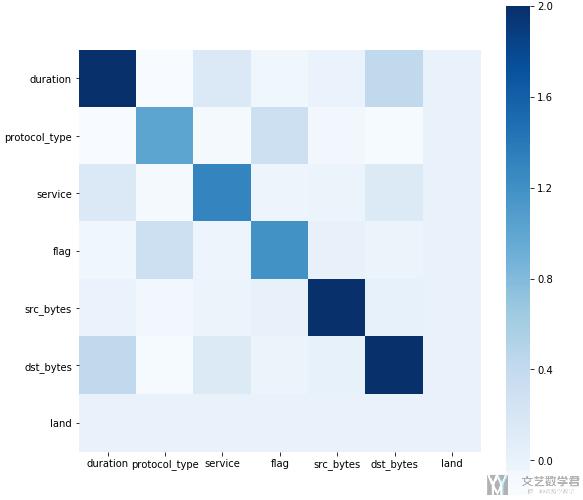
  8. sns.heatmap(dfData,square=True, cmap="Blues")

上面代码的绘制效果如下所示：

Python科学运算–简单汇总

 

数据预处理

  1. from sklearn import preprocessing

首先介绍一下标准化的几个式子，下面截图来自知乎：

Python科学运算–简单汇总

一般把第一种叫做归一化,第三种叫做标准化。关于详细的介绍，可以查看知乎的链接，标准化和归一化什么区别？

StandardScaler

在sklearn中，可以有两种方式进行实现数据的标准化，分别是使用函数scale和使用类StandardScaler()，下面分别来看一下：

使用scale进行计算：

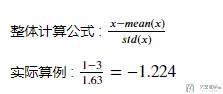
Python科学运算–简单汇总
  1. x_tt = np.array([[1,2],[3,4],[5,6]])
  2. preprocessing.scale(x_tt.astype(float))

我们看一下实际的计算结果

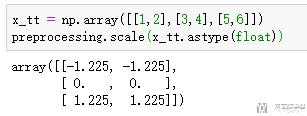
Python科学运算–简单汇总

当然，我们可以使用StandardScaler()来进行计算，使用这种方式可以查看每一维特征的均值和方差。

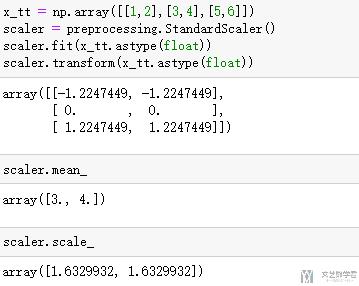
Python科学运算–简单汇总

Normalize

计算的步骤我用注释的方法写在了代码下面。

  1. x_tt = np.array([[1,2],[3,4],[5,6]])
  2. preprocessing.normalize(x_tt.astype(float))
  3. # 1/np.sqrt(1+4)=0.447
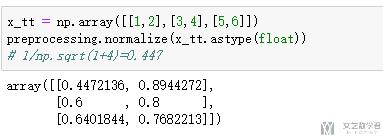
Python科学运算–简单汇总

Label的生成

有的时候我们的数据集中的label是string类型的, 例如是"paris", "paris", "tokyo", "amsterdam", 但是实际在训练的时候, 我们需要将其转换为long类型的. 这个时候就可以使用sklearn.preprocessing.LabelEncoder. 下面看一下简单的用法:

  1. from sklearn import preprocessing
  2. le = preprocessing.LabelEncoder()

接着对于我们要转换的数据, 使用fit函数.

  1. le.fit(["paris", "paris", "tokyo", "amsterdam"])
  2. # >> LabelEncoder()

我们可以查看有多少种不同的classes.

  1. list(le.classes_)
  2. # >> ['amsterdam', 'paris', 'tokyo']

接着我们可以对原始数据进行转换. 将string类型的label转换为int类型的.

  1. le.transform(["tokyo", "tokyo", "paris"])
  2. # >> array([2, 2, 1]...)

同时我们也可以逆向转换, 将index再转换为string类型的label.

  1. list(le.inverse_transform([2, 2, 1]))
  2. # >> ['tokyo', 'tokyo', 'paris']

 

离散变量变为标号(可以不用看, 使用上面的LabelEncoder代替)

有的时候，我们会将离散变量转为标号的表示（大部分情况会变为one-hot编码，转为one-hot的方式在下面介绍）

首先生成我们需要的测试数据：

  1. test = pd.DataFrame(np.array([[1,'a'],[2,'b'],[3,'a']]),columns=['X1','X2'])
  2. test
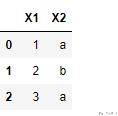
Python科学运算–简单汇总

我们首先看一下X2的类型，可以看到是object，我们可以将其转换为category.

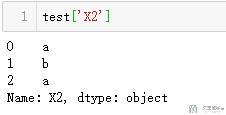
Python科学运算–简单汇总
  1. test['X2']=test['X2'].astype('category')
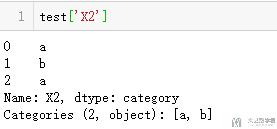
Python科学运算–简单汇总

接着我们就可以将其变为数字标号了。

  1. test['X2']=test['X2'].cat.codes
  2. test
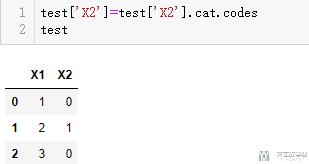
Python科学运算–简单汇总

下面放一下完整的片段

  1. test = pd.DataFrame(np.array([[1,'a'],[2,'b'],[3,'a']]),columns=['X1','X2'])
  2. test = test.astype('category')
  3. for i in test.columns:
  4.     test[i] = test[i].cat.codes

One-hot编码

对于离散得特征，我们通常会将他们转换为one-hot编码得形式，我们可以使用pandas完成相关得操作。下面是一个简单得例子。

  1. # 转为one-hot编码
  2. labels = ['a','b','c','d','d','a']
  3. pd.get_dummies(labels)
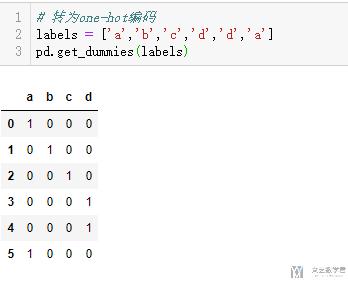
Python科学运算–简单汇总

我们也是可以设置drop_first=True来是的N维的特征使用N-1维来进行表示. 我们来看一个简单的例子. 比如说, 现在一个离散特征有三个取值, a, b, c. 那么我们只需要二维就可以表示 (二维应该可以表示2^2不同的组合, 但是这里不同有多个1同时出现).

  • a: [0, 0]
  • b: [1, 0]
  • c: [0, 1]

下面我们实际来举一个例子.

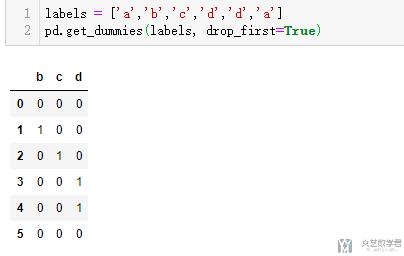
  1. labels = ['a','b','c','d','d','a']
  2. pd.get_dummies(labels, drop_first=True)

于是我们得到了下面的结果, 一共有a,b,c,d四种组合, 这里用三维的one-hot向量进行表示:

Python科学运算–简单汇总

 

关于One-hot的一点进阶说明

在使用pd.get_dummies将离散数据转换为one-hot的时候, 若原始数据集中包含其他类型的数据, 是否得到保留, 所以我们可以对整个数据直接进行pd.get_dummies, 我们看下面的例子.

在a中, X1和X2是连续型的, X3是离散型的, 我们只需要对X3进行转换.

  1. a = pd.DataFrame(np.array([[1.1,1.2,'a'],[2.9,2.0,'b'],[3,3,'a']]),columns=['X1','X2','X3'])
  2. a['X1'] = a['X1'].astype(float)
  3. a['X2'] = a['X2'].astype(float)
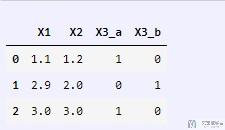
  4. pd.get_dummies(a)

最终的结果如下所示, 可以看到X1和X2是不会改变的.

Python科学运算–简单汇总

抽样与乱序

有的时候，我们需要在样本中进行抽样，或是打乱样本的顺序，我们可以使用如下的方式进行操作。

我们使用下面的数据进行一下实验：

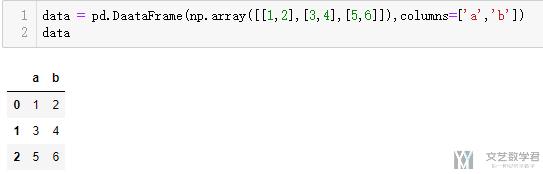
  1. data = pd.DaataFrame(np.array([[1,2],[3,4],[5,6]]),columns=['a','b'])
  2. data
Python科学运算–简单汇总

抽样

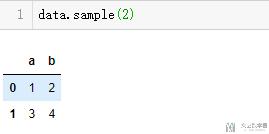
我们可以抽指定个数的样本：

  1. data.sample(2)
Python科学运算–简单汇总

也可以抽取指定比例的样本：

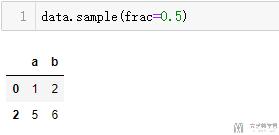
Python科学运算–简单汇总

乱序

想要进行打乱样本的顺序，我们只需要进行比例为1的抽样即可：

  1. data.sample(frac=1)
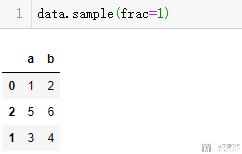
Python科学运算–简单汇总

乱序之后, 我们还需要对index进行重新的排序, 方法如下所示:

  1. test.reset_index(drop=True, inplace=True)

 

划分训练集和测试集

我们使用sklearn.model_selection.train_test_split来进行训练集和测试集的划分. 下面是简单的使用.

  1. import numpy as np
  2. from sklearn.model_selection import train_test_split
  4. X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

 

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2019年3月30日20:40:58
  • 转载请务必保留本文链接：https://mathpretty.com/10237.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: