文章目录(Table of Contents)
简介
在这一篇中我们会简单介绍一些常用分布的概率密度函数(pdf)和累计分布函数(cdf),同时使用 matplotlib 将其进行可视化。
参考连接
- 常用离散分布(介绍一些离散分布)
- 常用连续分布(介绍一些连续分布)
- 随机变量和3F(PDF、CDF、PMF)
PDF 和 CDF 的介绍
概率密度函数(probability density function, pdf)通常用来描述连续随机变量的概率分布。可以得到连续变量去某个值时,他的概率是多少。
我们可以使用在 scipy.stats 中使用不同的概率分布,例如我们可以计算正态分布 N(0, 1) 在 P(x=1) 时候的值,这里使用 norm.pdf 来计算:
- from scipy.stats import norm
- mean = 0
- std = 1
- norm.pdf(0, mean, std)
- """
- 0.3989422804014327
- """
有的时候我们需要计算 down<x<up 的概率,或是 x<X 的概率,这个时候直接使用 pdf(概率密度函数)计算比较麻烦(需要计算面积,积分)。
为了便于计算概率,我们引入累积分布函数 (cumulative distribution function)。例如我们希望计算正态分布 N(0, 1) 在 F(x=1)=P(x<1) 时候的值,则会有:
- mean = 0
- std = 1
- norm.cdf(1, mean, std)
- """
- 0.8413447460685429
- """
这里 F(x=1)=P(x<1) 表达的意思就是计算下图阴影的面积:
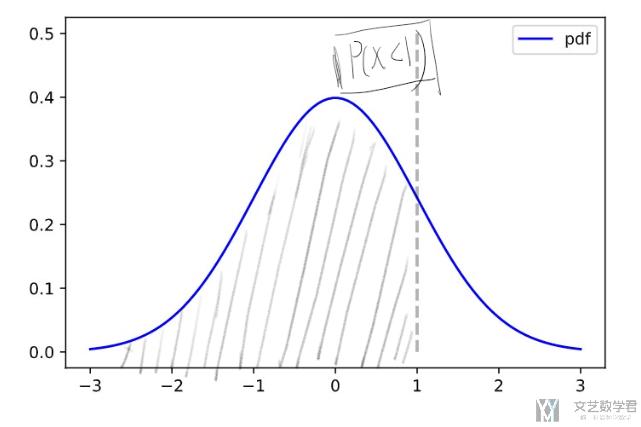
使用 Matplotlib 可视化 pdf 和 cdf
上面我们分别介绍了 pdf 和 cdf,下面来对其进行可视化。我们会对不同的连续分布的 pdf 和 cdf 进行可视化。
正态分布
我们利用上面介绍的 norm.pdf 和 norm.cdf 来生成指定的值,并绘制为折线图。
- # 绘制 pdf 和 cdf 的函数
- mean = 0
- std = 1
- fig = plt.figure()
- ax = fig.add_subplot(1,1,1)
- x_index = np.linspace(-3, 3, 100)
- data_pdf_data = [norm.pdf(i, mean, std) for i in x_index] # pdf 数据
- data_cdf_data = [norm.cdf(i, mean, std) for i in x_index] # cdf 数据
- ax.plot(x_index, data_pdf_data, color='b', label='pdf')
- ax_twin = ax.twinx() # 次坐标
- ax_twin.plot(x_index, data_cdf_data, color='g', label='cdf')
- ax.legend()
- ax_twin.legend()
最终的结果如下所示,这里正态分布的均值为 0,方差为 1。
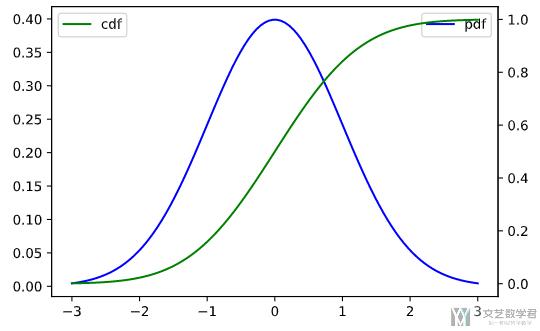
均匀分布
同样,我们只需要修改为 uniform.pdf 和 uniform.cdf 就可以绘制出均匀分布的 pdf 和 cdf 的图像。需要注意的是,这里设置的 loc 表示的为起点,scale 表示终点,最终的 uniform distribution 的范围是在 [loc, loc+scale].
- from scipy.stats import norm, uniform
- # ########################
- # 绘制均匀分布的 pdf 和 cdf 的函数
- # ########################
- loc = 0
- scale = 6 # [loc, loc + scale]
- fig = plt.figure()
- ax = fig.add_subplot(1,1,1)
- x_index = np.linspace(-3, 9, 100)
- data_pdf_data = [uniform.pdf(i, loc, scale) for i in x_index] # pdf 数据
- data_cdf_data = [uniform.cdf(i, loc, scale) for i in x_index] # cdf 数据
- ax.plot(x_index, data_pdf_data, color='b', label='pdf')
- ax_twin = ax.twinx() # 次坐标
- ax_twin.plot(x_index, data_cdf_data, color='g', label='cdf')
- ax.legend()
- ax_twin.legend()
最终的结果如下图所示,可以看到当 x 在 0-6 之间时,pdf 的值为固定值;cdf 在 x=6 的时候取值为 1:
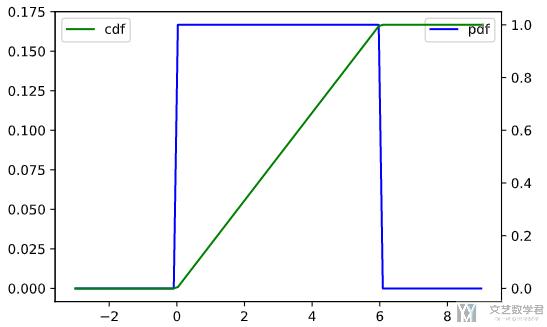
指数分布
指数分布只需要使用 expon.pdf 和 expon.cdf 即可。
- from scipy.stats import norm, uniform, expon
- # 绘制 pdf 和 cdf 的函数
- loc = 0
- scale = 2 # pdf = lambda * exp(-lambda * x), scale = 1 / lambda
- fig = plt.figure()
- ax = fig.add_subplot(1,1,1)
- x_index = np.linspace(0, 9, 100)
- data_pdf_data = [expon.pdf(i, loc, scale) for i in x_index] # pdf 数据
- data_cdf_data = [expon.cdf(i, loc, scale) for i in x_index] # cdf 数据
- ax.plot(x_index, data_pdf_data, color='b', label='pdf')
- ax_twin = ax.twinx() # 次坐标
- ax_twin.plot(x_index, data_cdf_data, color='g', label='cdf')
- ax.legend()
- ax_twin.legend()
最终的效果如下图所示:
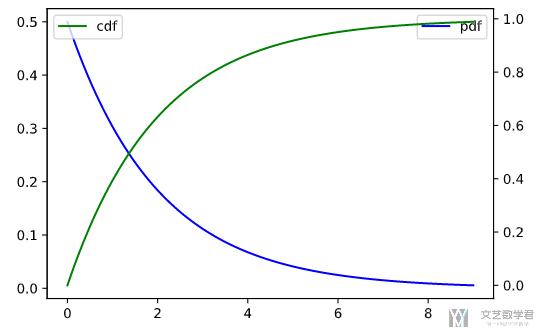
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-












评论