Deep TAMER: Interactive Agent Shaping in High-Dimensional State Spaces 阅读

简介

最近在看 Reinforcement Learning with Human Feedback (RLHF) 的相关内容，而其中本次要介绍的 Deep TAMER 就是其中一个相关工作，他尝试将人的判断加入到训练过程中，学出一个类似 Q-function 的函数（文章里面称为 Reward Fucntion）来进行决策。

目前的强化学习需要大量与环境交互探索才可以获得一个好的效果。为了提升效率，一个方法是在训练的输入中加入人工的数据。之前的工作（TAMER）已经证明了加入人工数据之后的优异表现，但是这些工作没有考虑复杂的 state 下的结果，也没有使用 deep learning。

于是本文做出了下面两个方面的贡献：

• We propose specific enhancements to TAMER that enable its success in high-dimensional state spaces in a framework we call Deep TAMER.
• We quantify the performance difference between TAMER and the proposed technique in an environment with high-dimensional state features. We demonstrate Deep TAMER's success by using it and just 15 minutes of human-provided feedback to train an agent that performs better than humans on the Atari game of BOWLING - a task that has proven difficult for even state-of-the-art reinforcement learning methods.

参考资料

• Paper：Deep TAMER: Interactive Agent Shaping in High-Dimensional State Spaces
• Github-Tamer，非官方实现的代码，可以参考一下 importance weight 的计算；
• Github，Awesome RLHF，Github 上关于 RLHF 资料的整理；
• Gymlibrary-Bowling，环境 Bowling 的介绍；

Deep TAMER 介绍

整体框架介绍

Deep TAMER 的整体框架如下图所示。在本文中，作者使用的是 Atari game - BOWLING 环境：

• 首先 human 对看到的 agent 的动作进行一个打分，对 agent 的行为进行改变（A human observes an autonomous agent trying to perform a task in a high-dimensional environment and provides scalar-valued feedback as a means by which to shape agent behavior）；
• 根据 human 的反馈，agent 优化一个网络 H，H 的目的是预测人类的反馈，最后根据 H 可以得到一个策略（Through the interaction with the human, the agent learns the parameters of a deep neural network, H, that is used to predict the human's feedback. This prediction then drives the agent's behavior policy）；

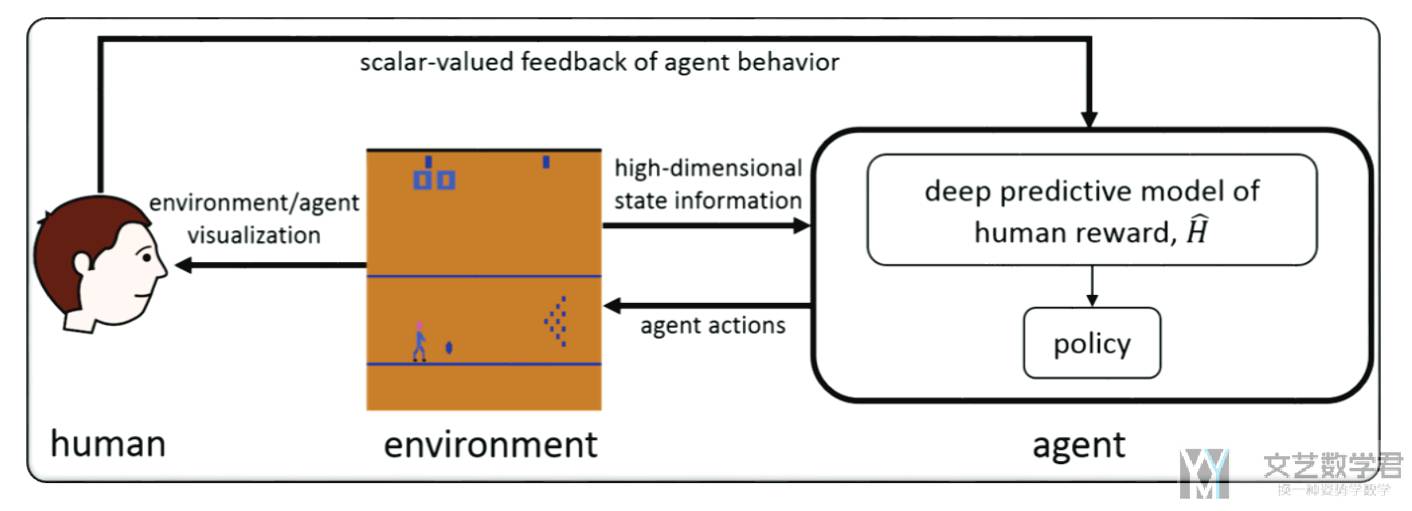
那么现在的问题就是，如何根据人类的反馈，来得到一个 human reward model，H。

Human Reward Model

这一部分我们讨论如何得到 reward function。假设 scalar-valued feedback signal 记为 h，这里 h 越大表示人对 agent 的动作越认可。我们假设人是根据当前 state 和 agent 做出的 action 给出的打分，也就是 H(s,a)，我们希望去拟合 H(s,a) 函数。当有了 H(s,a) 之后，就可以根据下面的式子得到策略（我感觉这里的 H(s,a) 和 Q(s,a) 非常像）：

于是问题就变为了一个有监督的问题，现在我们有输入 x=(s,a,t_s, t_e)，其中 t_s 是 state 的时间，t_e 是 action 的时间，输出是人类的反馈 y = (h, t_f)，t_f 是接收到反馈的时间。我们记录这些时间是为了将这个反馈分配到不同的 state 和 action 时候要计算权重使用。于是 loss 函数可以写成下面的样子（问题转换为最小化下面的式子）：

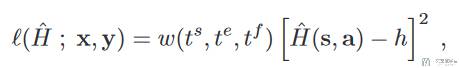
其中 w 是对每一个 x=(s,a,t_s, t_e) 和 y = (h, t_f) 的权重的系数。关于 w 的具体形式会在后面的 importance weight 的时候进行介绍。

Deep Reward Model 介绍

上面描述了如何去拟合 H(s,a)，这里介绍一下 H(s,a) 具体的结构。由于本文是处理高维的 state，因此作者使用了「神经网络」来进行处理，于是 H(s,a) 如下所示：

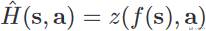
其中 f(s) 是 Autoencoder，可以使用随机的策略收集数据，然后进行预训练。Deep Autoencoder 中 encoder 部分如下所示。用于从输入的游戏画面中提取信息（这部分可以提前进行训练），在后面的训练中，这部分的参数会进行固定：

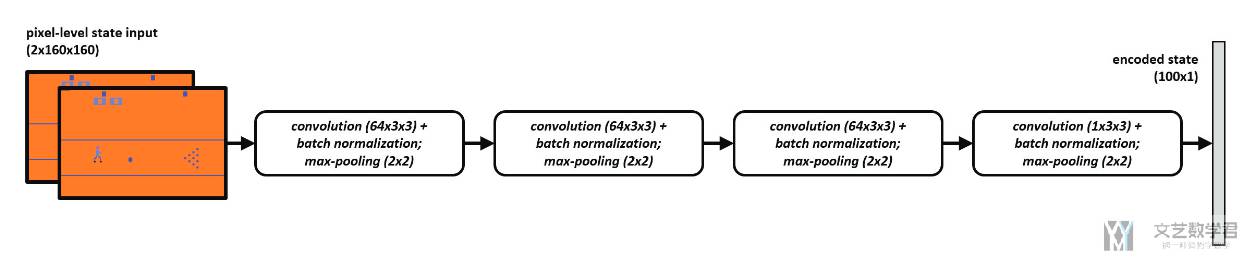
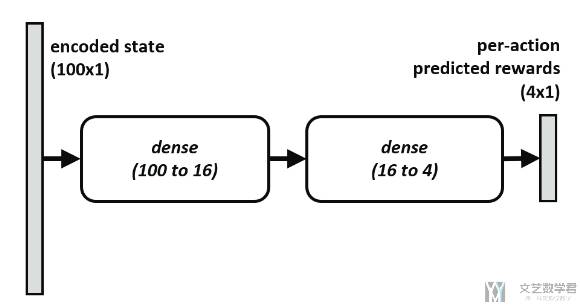
剩下的部分就是一个全连接网络，结构如下所示，可以看到此时的输入是 encoded state，也就是上面网络的输出。接着根据收集的人的反馈进行训练即可。注意这里作者将所有的反馈存储在 Feedback Replay Buffer 里面。

Importance Weights 介绍

在介绍「Human Reward Model」的时候，我们提到在计算 loss 的时候，需要对每一个 x=(s,a,t_s, t_e) 和 y = (h, t_f) 计算权重 w(t_s, t_e, t_f)，这一部分我们会详细介绍权重的计算。由于我们获得是一串 (s, a)，我们并不知道 human feedback 是给哪一个 (s, a) 的，于是就需要添加一个权重，这个权重需要满足：

• Human trainers intend for their feedback to apply only to recent agent behavior.
• w(t_s, t_e, t_f) 相当于是一个概率，t_f 时刻给的 feedback 是 (t_s, t_e) 的可能性；
• 当 t_f 小于 t_s 的时候，权重是 0，相当于 feedback 不会给后面的动作；
• 当 t_f 远远大于 t_s 的时候，权重应该很小；

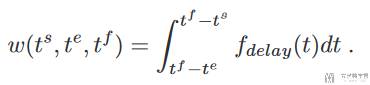
这里 f_delay 作者使用了均匀分布，U(0.2, 4)，这样 w 只有在 feedback 前 0.2-4s 之间权重 w 不为 0，其他的权重都是 0。

下面我们来看一个具体的例子，假设在 4s 的时候接收到反馈，人的反映时间差不多是在 1-3s 之间，我们想要计算 0-8s 之间的每个时间分到这个反馈的概率。计算的代码如下所示：

运行上面的代码，可以得到如下的结果。可以看到当接收到 feedback 的时间是 4s 的时候，我们认为这个反馈是给 1-3s 之间的 state 和 action 的。相当于减去 1-2s 的人类反应时间，所以 credit 比较高的点在 1-3s 之间。

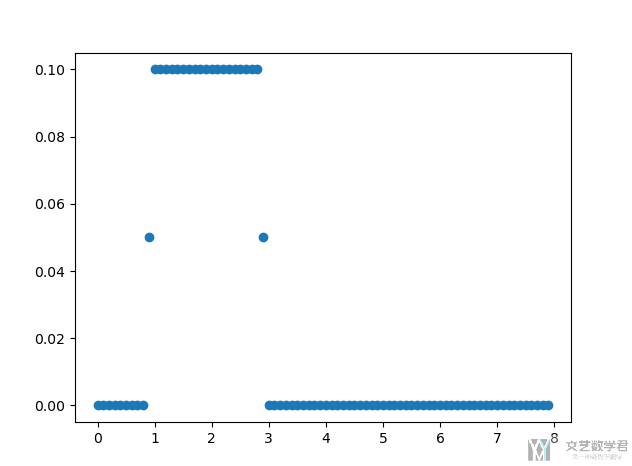
关于这里为什么使用均匀分布 U(1, 3)（这里 scipy 中的 uniform(loc, scale) 是均匀分布 [loc, loc+scale]），作者进行了一个简单的解释。这个与环境有关，这里使用的是 BOWLING 这个环境，通常在 agent 做出动作后 1-2s  内人类才会给出反馈，因为需要根据保龄球撞击的结果进行判断。

实验结果

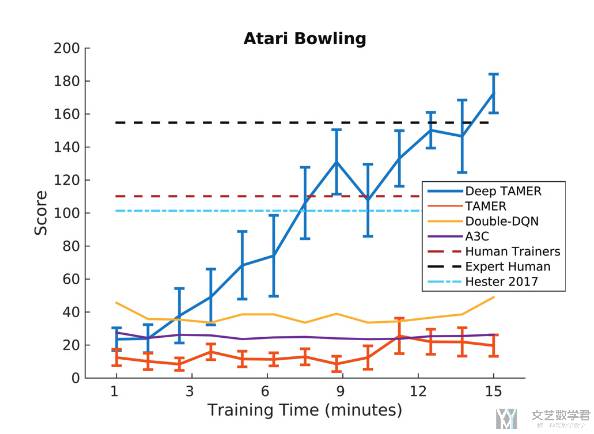
作者的实验在环境 Atari game of BOWLING 上进行。作者和当时性能最好的强化学习算法比较，结果如下图所示，可以看到 Deep TAMER 的平均游戏得分可以高于其他的方法。注意这里作者只训练了 15 分钟，因此 A3C 和 DQN 都是无法很好收敛的。