【多智能体强化学习】QMIX 论文笔记

简介

本文是介绍多智能体强化学习值分解中的 QMIX 算法。关于 VDN 算法的解释，可以查看 【多智能体强化学习】VDN 论文笔记。

QMIX 可以理解成是在 VDN 上面进行了改进。在 VDN 中，我们简单的将每个 agent 的 Q 值相加，得到最后的 Q_tot。但是在 QMIX 中，我们拓展了更多的组合，这里作者提到，只要是系数是正数的组合都是可以的，所以在 QMIX 中希望可以使用网络去学习一组系数将每个 agent 的 Q 值组合起来，得到 Q_tot。

与 VDN 相比，QMIX 改进了联合Q函数的形式，融合了部分全局信息，使得模型的性能有很大的提升。这里需要注意的是，agent networks 并没有使用全局信息，所以这还是一个 POMDP 环境。

参考资料

• Cooperative Multi-Agent Reinforcement Learning，介绍了 QMIX 算法；
• QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning，论文原文；
• epymarl--qmix，QMIX 的代码实现，可以进行参考。

QMIX 算法解读

目前研究的进展

在多智能体研究中，由于部分可观测性或通信上的限制，我们需要学习只依赖于每个AI智能体各自的局部动作和观测历史的分散式策略（Decentralised policies）。这种策略能有效缓解一个问题：随着AI智能体数量的增加，联合动作空间呈指数级增长，这通常使得传统的单一智能体强化学习（RL）方法变得不切实际。

在模拟或实验室环境中，通常可以集中式地学习这些分散式策略（我理解是可以有一个 Q_tot 或是可以集中训练一个 critic network）。这样做通常能够获取到额外的状态信息，这些信息在平常情况下对智能体来说是不可见的，并且还能消除智能体间的通信限制。集中式训练与分散式执行（centralised training with decentralised execution）的模式最近在 RL 领域引起了广泛关注。然而，如何最佳利用集中式训练的问题仍然没有得到解决。

其中一个挑战是如何表示和利用大多数 RL 方法都会学习的动作价值函数。一方面，为了正确反映智能体的动作效果，我们需要一个依赖全局状态和所有智能体共同动作的集中式动作价值函数 Q_tot。另一方面，当智能体数量众多时，这样的函数很难学习，而且即便能够学习到，也没有明显的方法来提取允许每个智能体仅基于个别观测来选择动作的分散式策略（即将 Q_tot 分解到每一个 agent 上，来使其可以作出动作）。

最简单的方法是不采用集中式动作价值函数，而是让每个智能体分别学习一个独立的动作价值函数Q，例如独立Q学习（Independent Q-Learning，IQL）那样。但这种方式无法明确表示智能体之间的交互作用，并且可能不会收敛，因为每个智能体的学习都会受到其他智能体学习和探索的干扰。

在另一个极端，我们可以学习一个完全集中的状态动作价值函数 Q_tot，并用它来引导 Actor-Critic framework 中分散式策略的优化。这种方法被反事实多智能体策略梯度（Counterfactual Multi-Agent Policy Gradients，COMA）的研究中采用。然而，这种方法需要基于策略的学习，可能效率低下，并且当智能体数量稍多时，训练一个完全集中的评论家变得不现实。

QMIX 的主要思路

于是就有了 QMIX 这种新方法。这种方法介于 IQL 和 COMA 之间，与价值分解网络（VDN）相似，但能表征更为丰富的 Q function。QMIX 方法的核心见解在于，为了提取分散式策略，并不需要像 VDN 那样进行完全分解。QMIX 的目标是确保对总体动作价值函数 Q_tot 执行全局最优化操作（global argmax）所得到的结果与对每个智能体的个别动作价值函数 Q_a 执行的个别最优化操作（individual argmax）相同。也就是希望下面这个式子成立：

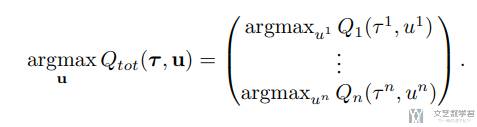
这样，只需要每个 agent 贪婪的进行选择，得到的结果也可以满足全局最优。为了达到这个目的，需确保 Q_tot 与每个 Q_a 之间的关系满足单调性约束，也就是满足下面的式子：

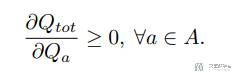
总结来说：

• QMIX 包括代表各自 Q_a 的智能体网络，以及一个混合网络，后者不是简单地将它们相加得到Q_tot，而是通过复杂的非线性方式进行组合，以确保集中化策略和分散化策略之间的一致性。
• 同时，为了满足前述的约束条件，混合网络被限制只能使用正权重。因此，QMIX能够用分解的形式表达复杂的集中化动作价值函数，这种形式随着智能体数量的增加而良好扩展，并且可以通过简单的个别最优化操作，即在计算上是线性时间内完成的操作，轻松地提取出分散式策略。

QMIX 的网络结构

于是为了实现上面的想法，QMIX 作者设计了如下的网络结构：

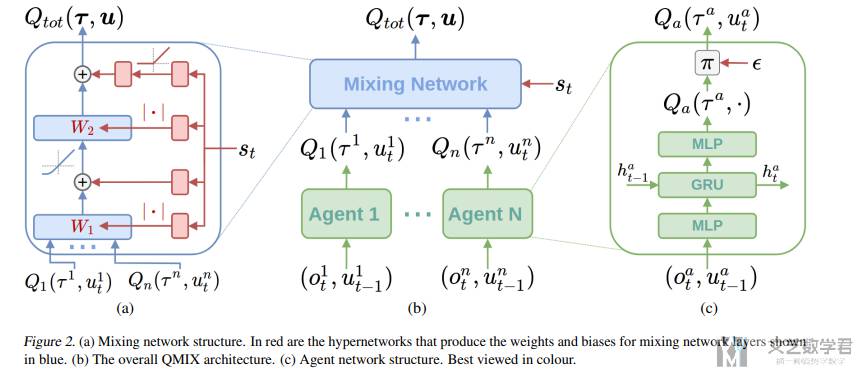
上面的网络结构分为三个部分：

• agent network：每一个 agent 都需要独立去学一个值函数 Q，这里的 o 是当前的观测，u 是上一步的动作。之后决策的时候只需要依赖这个 agent network，因此只需要每个 agent 自己的观测即可，不需要全局信息；
• mixing network：这是一个全连接网络，接受每个智能体的值函数 Q，输出联合动作函数 Q_tot。这里对每个子智能体的动作值函数做非线性映射，并且要保证单调性约束，也就是 mixing network 的权重非负即可。
• hyper network：hypernetworks 网络去产生 mixing network 的权重，超参数网络输入状态，输出 Mixing 网络的每一层的超参数向量，激活函数来使得输出非负，对于 Mixing 网络参数的偏置并没有非负的要求（我的理解，这里相当于希望结合全局信息 s，给每个 Q 生成一个权重，然后因为是生成的是权重，所以称为 hypernetworks）。

在有了 Q_tot 之后，QMIX 的训练方式就和常规的 Q Learning 是一样的，也是采用端到端的训练方式，如下所示：

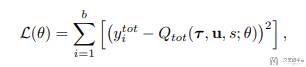
QMIX 的局限性

这里简单说明一下 QMIX 的局限性（最后那部分关于单调性的我也不是看得很懂）。就是在多智能体合作的时候，某个智能体的最佳行为可能取决于其他个体的行为。

为了解释非单调回报矩阵，我们可以使用一个简单的两步游戏来举例。假设有两个智能体（Agent A和Agent B），它们需要在两个连续的决策点上做出选择。每个决策点上，每个智能体都可以选择合作（C）或背叛（D）。智能体的目标是最大化它们的总回报。

我们可以构建一个简单的回报矩阵来表示第一步的回报，例如：

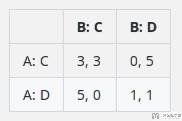
在这个矩阵中，如果两个智能体都选择合作（C,C），他们都获得3点回报。如果一个智能体选择合作而另一个选择背叛（C,D或D,C），背叛者获得5点，合作者获得0点。如果两者都背叛（D,D），他们各自获得1点。

现在，假设第二步的回报矩阵取决于第一步的行为。如果在第一步中至少有一个智能体选择了背叛，那么第二步的回报矩阵可能看起来这样：

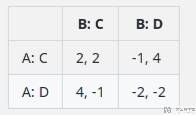
在这个矩阵中，如果在第一步中有背叛发生，合作的价值就会降低（因为信任已经被破坏），而背叛可能导致更高或更低的回报，这取决于另一个智能体的行为。

如果在第一步中没有智能体选择背叛，第二步的回报矩阵可能会鼓励合作，例如：

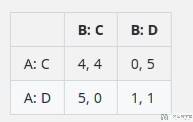
在这种情况下，持续的合作会带来更高的回报，但背叛仍然可能会发生，尤其是如果一个智能体试图在最后一刻背叛以获得短期利益的话。

QMIX 通过其设计保证了全局价值函数对于任何个体智能体的 Q 值是单调的。然而，如果全局最优策略需要在某些情况下降低某个智能体的 Q 值（例如，为了长期的合作而短期牺牲），QMIX 可能无法学习这种策略。这是因为它的结构不允许全局价值函数对任何个体智能体的 Q 值表现出非单调性。因此，QMIX 可能无法捕捉到在第一步行动后，第二步回报结构变化所需的策略复杂性。

在上述游戏中，智能体的最佳策略可能涉及在第一步中牺牲立即的回报，以便在第二步中获得更好的结果。这种策略可能需要智能体在某些情况下选择减少自己的立即回报（例如，选择合作而不是背叛），即使这会导致它们的 Q 值降低。由于QMIX 的设计，它可能无法正确学习这种需要非单调策略变化的情况。

QMIX 的代码实现

下面来看一下 QMIX 中 mixing network 和 hypernetworks 的代码实现。我们结合上面的图(a) 的区域，可以看到有两层（这里为全连接层），我们会分别对这两层进行分析。

Mixing Network 第一层

第一层的式子可以写为：hidden = agent_qs * w1 + b1，这里 agent_qs 就是每一个 agent 的 Q value，w1 是用于对 agent_qs 加权的系数，这里 w1 是根据全局信息得到的，且需要为正数。

于是我们可以定义 w1 和 b1 的网络如下所示。输入大小是全局观测的维度，输出大小是希望转换的维度。同时 w1 需要考虑到每一个 agent 都有 Q，所以输出维度要乘 n_agents。

于是我们可以分别计算 w1 和 b1，接着计算得到 hidden 的值。需要注意这里 w1 通过 torch.abs 使得其数值一定是正数。

例如现在 agent_qs 的大小是 (B, 1, 4)（也就是有四个 agent，最后一个维度是 4），那么 w1 的维度是 (B, 4, 32)（这里 32 就是 embed_dim），b1 的大小是 (B, 1, 32)，这样最后输出的维度是 (B, 1, 32)，相当于把 4 个 Q 值进一步分解为 32 个。

下面的图展示了假设此时有 4 个 agent，那么就会有 4 个 Q 值，此时的 w1 的大小是 (4, 32)，b1 的大小是 (1, 32)。这里的 w1 和 b1 是由网络生成的，也就是 hypernetworks。

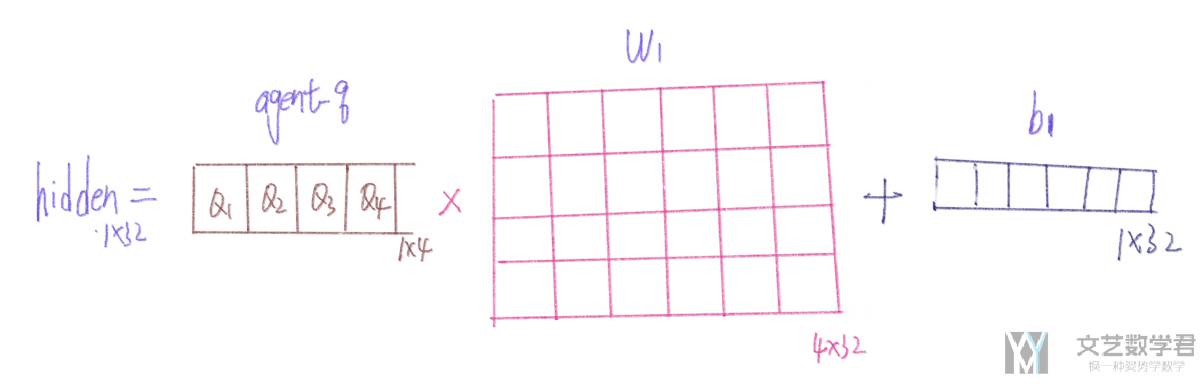
Mixing Network 第二层

第二层：q_total = hidden * w2 + b2，与第一层类似， w2 和 b2 也是有网络生成的。这里的 V 就是 b2。

还是根据全局的信息来分别计算 w_final（对应 w2） 和 v（对应 b2）。最后计算 y，就是 Q_total。同样，这里的 w_final 也需要使用 torch.abs 使得其数值一定是正数。

还是接着第一层的例子，此时 hidden 的大小是 (B, 1, 32)。那么 w_final 的大小就是 (B, 32, 1)，而 b2 的大小是 (B, 1, 1)，于是最后输出的大小是 (B, 1)，也就是 Q_total。下图还是接着上面的例子，计算出最终的 Q_total（是一个数字）。

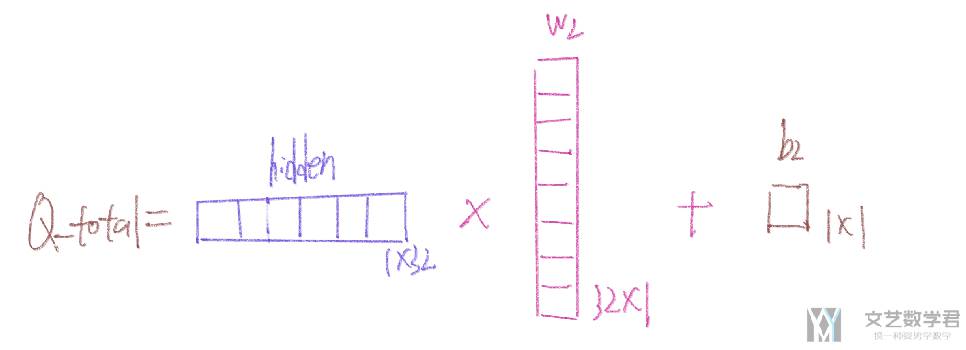
这里需要注意，全局信息是用于计算 Q 的权重的，而不是直接用于计算 Q_total 的。