如果地球是圆环

最近在看点集拓扑的时候，看了一本介绍庞加莱猜想的书--<庞加莱猜想--追寻宇宙的形状>，作者：[日]春日真人，感觉很有意思。

这是根据纪录片改编的书，要看纪录片可以看这个链接，里面有百度网盘提供下载： http://bbs.crsky.com/read.php?tid=3023122

上面那个网址现在已经打不开了，我就直接放百度网盘的链接。

地址：https://pan.baidu.com/share/init?surl=hrC2BAk

密码：iytg

下面是我觉得书中有一些话很有意思，做一些摘录。

书中摘录

1519年，麦哲伦环游地球，向世人首次证明了我们日常生活中看到的平的地球实际是巨大球体的一部分。在麦哲伦航海成功400年后，数学家亨利庞加莱提出了不同的想法，他认为麦哲伦的方法根本无法证明地球是球形的。庞加莱是这样推论的，“如果地球不是完美的球形又如何，假设存在一个贯穿南北极的巨大孔洞，地球就想一个甜甜圈，那么在这种情况下，麦哲伦的船队也能回到最初出发的地点”。 这个怀疑也许会被许多人认为无稽之谈，但是在庞加莱生活的那个年代，也就是19世纪后半叶和20世纪初，别说是人造卫星，就连飞机都还没发明出来（1903年12月14日至17日莱特兄弟的飞机能完成留空时间最长59s，到1906年，他们的飞机在美国获得专利发明权）。当时还没有人能够亲眼看到南北极，事实上，要等到1909年，美国人罗伯特皮特才第一个到达北极点，南极点则是1911年挪威人罗阿尔德阿蒙森第一个到达的，也就是说，贯穿两个极点的巨大孔洞是否存在当时谁也无法证明。

我们可以看一下如果地球是甜甜圈，那会是什么样子的，下面会有代码来实现这个图。

而庞加莱猜想是，如果当船出发时将一条绳子的一头绑在船上，一头绑在岸上，当船环游一周回到原点的时候，如果能收回绳子，那么能证明地球是球形的，如果不能收回绳子，就证明地球不是球形的。

如今我们已经知道了地球的形状，但是我们想要探求宇宙的形状，其实，我们也可以采用和地球完全一样的方法来探求宇宙的形状，如果绳子能完全收回的情况下，就与地球实验相同，宇宙也不应该存在孔洞或裂缝。

在地球表面爬行的蚂蚁，很难知道地球的形状，因为他离不开地球表面，同样，人类现在也还无法到达宇宙之外，但是，庞加莱提出了他的猜想，即使人类无法到达宇宙之外，也应该有线索可以让我们探求宇宙的形状。

下面这个是纪录片中的截图

如果宇宙是甜甜圈的形状，绳子是无法被收回的，如上图所示，绳子在收回过程中一定会遇到不再甜甜圈表面的情况。

关于庞加莱猜想 首先是庞加莱猜想原本的表述：任何一个单连通的，封闭的三维流形都与三维球面同胚

下面我们来试着解释一下：

1. 单连通：是指其表面的绕绳子，一定能全部收回
2. 封闭的三维流形：四维空间的表面
3. 三维球面：四维球形空间的表面
4. 同胚：等同

将这些词去替换上面的原本的定义，就能更好理解什么是庞加莱猜想了。

下面是一段写在论文--On Proof and Progress in Mathematic里的话：

“我误以为周围的学者都在热切期盼答案的出现，我当时一厢情愿的以为如果`自己能给出很多强有力的证明结果的话，对其他数学家也是好事，但是事情不是这样的。大家追求的不是答案本身，而是如何进行思考的过程。”

下面我来讲一下如何画出甜甜圈的形状和如果地球像甜甜圈一样会是什么样子的。

圆环的参数方程

我们首先来画出圆环，关于圆环的参数方程可以看下面的图

于是我们可以通过上面的参数方程画出圆环的样子。

ParametricPlot3D[{(R + r Cos[v]) Cos[u], (R + r Cos[v]) Sin[u], r Sin[v]}, {u, 0, 2 Pi}, {v, 0, 2 Pi}, Mesh -> None]

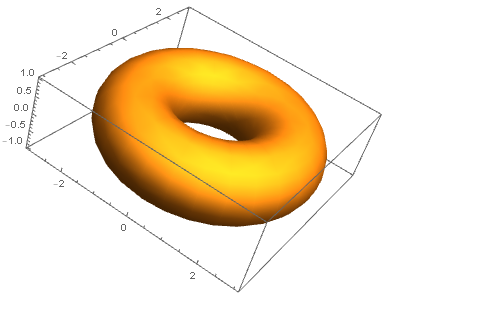
如果地球是圆环状

下面我们来将地球的图片作为纹理印在圆环上，下面代码是不能运行的，因为需要在Texture[]里增加一个地球的图片，我直接给出画出的效果。

R = 2;
r = 1;
ParametricPlot3D[{(R + r Cos[v]) Cos[u], (R + r Cos[v]) Sin[u],
r Sin[v]}, {u, 0, 2 Pi}, {v, 0, 2 Pi},
Mesh -> None,
PlotStyle -> Texture[],
Boxed -> False, Axes -> False
]

让我们的地球转起来

可以看到如果地球是圆环，那么应该是上面图中的样子，下面我们让这个地球转起来。同样代码是不能运行的，需要在Texture[]里增加一个地球的图片，我直接给出画出的效果。

R = 2;
r = 1;
pic = Table[
ParametricPlot3D[{(R + r Cos[v]) Cos[u], (R + r Cos[v]) Sin[
u], -r Sin[v]}, {u, 0, 2 Pi}, {v, 0, 2 Pi},
Mesh -> None,
Boxed -> False, Axes -> False,
ViewPoint -> {x, -N[Sqrt[4^2 - x^2]], 3},
ImageSize -> {200, 200}
], {x, 4, -4, -.5}];
ListAnimate[pic]

一些其他的

如果大家对这个有兴趣的话，可以再读读下面的这篇文章。

大家可以参考一下果壳网的这篇文章：【what-if向】如果我们的地球是个甜甜圈

结语

最后用<庞加莱猜想--追寻宇宙的形状>的最后一句话作为结束

Mais cette question nous entrainerait trop loin 这个问题必将引领我们到达那遥远的世界