Mathematica提取边缘座标

这一篇文章会介绍一下如何使用Mathematica中的边缘座标，什么是边缘座标呢，我们先看一下下面的图片。

data = Flatten[Table[{x, x + 5*Sin[x] + RandomReal[2*j]}, {x, 0, 10, .1}, {j, 1, 10}], 1];
ListPlot[data]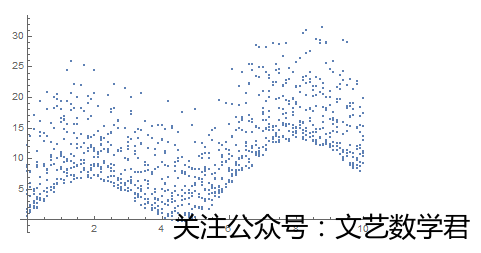

数据的样子如上图所示，我们要找出一些边缘的点，我们可以使用函数ConvexHullMesh。

Show[ConvexHullMesh[data], Graphics[Point[data]]]

我们来获得边缘点的座标

zb = MeshCoordinates[ConvexHullMesh[data]];
Length[zb]
>> 30

可以看到一共有30个座标点。

我们把边缘座标在图中显示出来

Show[ConvexHullMesh[data], Graphics[{Red, PointSize[Large], Point[zb]}]]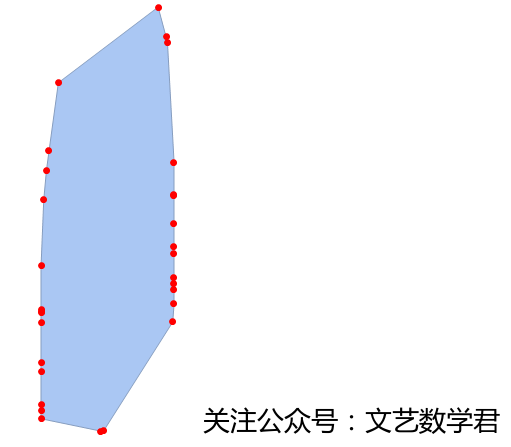

下面我们来获取上面最高的两个点的座标，当然要是想获取这两个点的座标最简单的方法就是按照y的值排序即可，但是我们这里就是不这样来做，我们换一个思路。

SortBy[zb, #[[2]] &][[;; 2]]
>> {{4.5, -0.320249}, {4.7, -0.298881}}

可以看到最低点的横座标大概在4 .5 左右，故我们一4 .5 为分界

zb2 = GatherBy[zb, #[[1]] > 4.5 &]
Show[ConvexHullMesh[data], 
 Graphics[{Red, PointSize[Large], Point[zb2[[1]]]}], 
 Graphics[{Green, PointSize[Large], Point[zb2[[2]]]}]]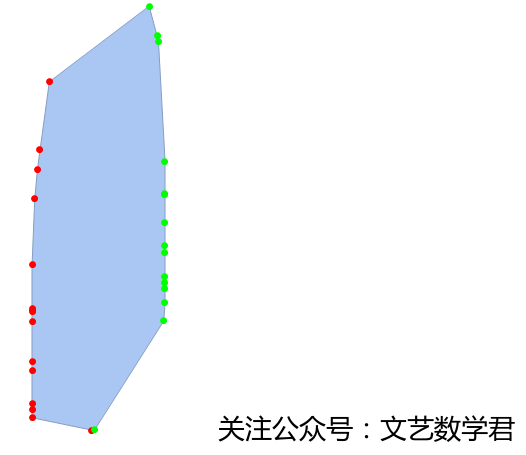

可以看到成功把所有两边的点分开了，下面我们来找出各自的最高点

maxzb = MaximalBy[#, #[[2]] &] & /@ zb2
>> {{{1.3, 25.8798}}, {{8.8, 31.5633}}}
Show[ConvexHullMesh[data], 
 Graphics[{Red, PointSize[.2], Point[maxzb[[1]]]}], 
 Graphics[{Green, PointSize[.2], Point[maxzb[[2]]]}]]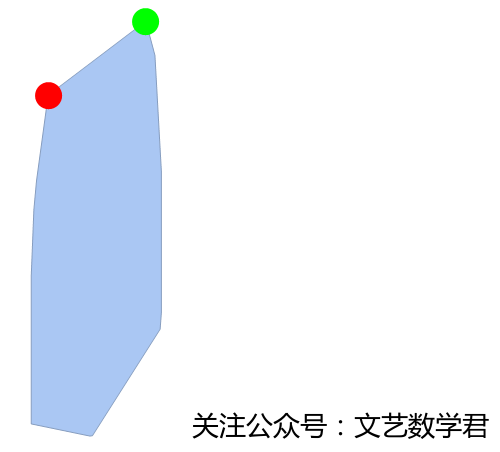

这样我们就完成了上面我们要做的一些工作了，还是很不错的。