注意力机制

简介

本文会介绍「注意力机制」的相关内容。主要会介绍「非参注意力机制」和「带有参数的注意力」。这里均使用一维数据作为例子。通过会介绍什么是「注意力分数」，这在后面会被反复使用到。

参考资料

• Attention Mechanisms（注意力机制），本文的相关代码（包含「非参数注意力」和「参数注意力」两个部分的代码）；
• 动手学深度学习在线课程，包含完整的课程大纲；
• 64 注意力机制【动手学深度学习v2】，B 站视频；

注意力机制

注意力机制会去建模「随意线索」。随意线索会被称为「query」，环境是「key-value pair」。注意力池化会根据「query」，去有选择的挑选「key-value」。也就是如下图所示：

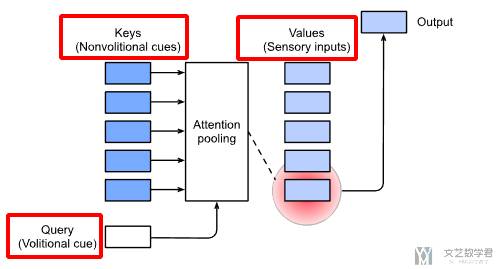
非参注意力池化层

例如现在给定数据 (x_i, y_i), i=1,2,...,N，这里 x_i 相当于是 key，y_i 相当于是 value。这里就是给定了 key-value 对。现在有一个查询值 x（query），请问他的 value 是多少。

最简单的方式就是把数据集里面所有的 value 全部求平均即可。不管查询的 x 是什么，都输出均值。也就是下面的式子所表达的：

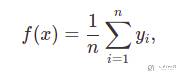
另外一个方式是将要查询的 x 和所有的 key-value 对中的 key 进行一个比较，也就是下面式子里面的K(x - x_i)。其中 K 是一个函数，用来衡量 x 和 x_i 之间的距离。

进一步对下面的式子进行解释，我们对每一个 x_i 都会计算一个权重，接着将这个权重乘上 x_i 对应的 y_i；遍历每一个 key-value 对，最终得到 query 的 value 值。

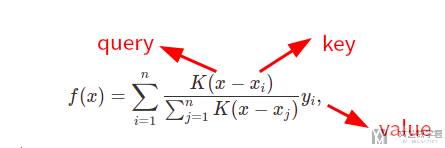
那么这个 K(x - x_i) 具体是什么了，或是选择什么来衡量 x 和 x_i 之间的距离。如果我们选择「高斯核」作为 K，如下面的式子所示，其中 u 表示 x-x_i。

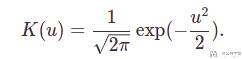
将上面的「高斯核」代入进行化简，会得到下面的式子。其中使用了 exp 的作用为把值变为大于 0 的值，下面除数相当于做了 softmax。式子中第一行的 α(x, x_i) 也被称为「注意力权重」。

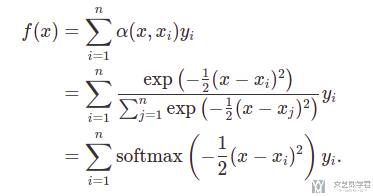
上面这个式子会和注意力机制非常像，区别就是目前这个式子是没有可以学习的参数的。

非参数注意力详细例子

这里我们来看一个具体的数值例子来理解「非参数注意力」。现在假设有：

• query为 {1,5,10}，有三个值需要被查询。这里 query 有一个值 5，是和下面key-value 对中出现的，希望此时就是返回 key=5 对应的 value=50。
• key-value 对为，{(5, 50), (15, 100)}，及有两个 key-value 对；

首先我们计算 query 与 value 之间的差值，也就是 x-x_i 的值。注意这里计算结果为大小为 3*2，如下所示。第一行相当于是将 query=1 分别减去两个 key，也就是 (1-5, 1-15)。

接着对每个 query 的值进行 softmax，如下图所示，可以看到每一行和为 1，也就是一个 query 对所有 key 的权重和为 1。

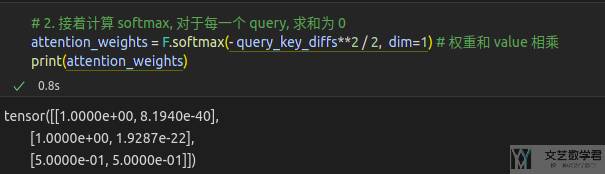
最后将上面得到的 attention weight 分别乘 key 对应的 value ，得到最终 query 的值：

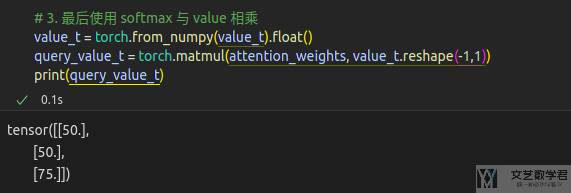
参数化注意力机制

我们可以加入一个可以学习的参数 w，使得上面的式子变得可以学习。下面是修改后的式子。后面会介绍更多关于权重的计算方式，也就是如何计算 α(x, x_i)（这个就是注意力权重）。

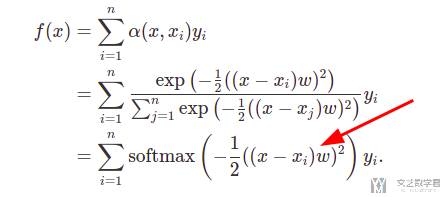
具体来说，我们可以使用 key-value pair 来作为训练的数据集，来训练得到参数 w。同时这个参数 w 就是加在了 x-x_i 后面，也就是 (x-x_i)*w。