文章目录(Table of Contents)
简介
在前面介绍的内容中,query 和 key-value pair 通常是不同的。而对于「自注意力」来说,query 和 key 和 value 都是相同的。也就是说,同一组词元同时充当「查询(query)」、「键(key)」和「值(value)」。(自注意力的关键就是一句话,查询、键和值都来自同一组输入)
每个查询都会关注所有的键-值对并生成一个注意力输出。 由于查询、键和值来自同一组输入,因此被称为「自注意力(self-attention)」。
参考资料
- 自注意力和位置编码,D2L 中文文档;
- Self-Attention and Positional Encoding,D2L 英文文档;
- 67 自注意力【动手学深度学习v2】, B 站视频;
- 多头注意力,文艺数学君,后面会用到「多头注意力」,将链接放在这里;
- Attention-mechanisms-and-transformers,后文会用到完整的代码,对应的文件是「selfAttention_and_positionEncoding.ipynb」;
自注意力
自注意力图解
对于「自注意力」,我们给定一个输入序列 (a1, a2, ..., an),该序列的自注意力输出为一个长度相同的序列 (b1, b2, ..., bn),如下图所示:
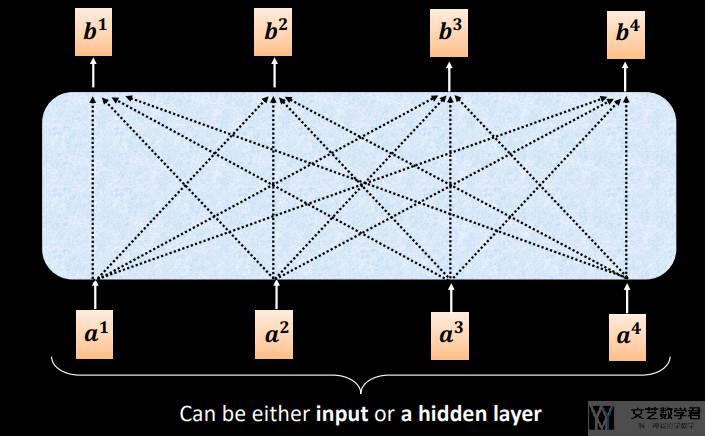
每一个 bi 的计算,相当于将对应的 ai 看作 query,与其他的 (ai, ai) 计算注意力。具体来说,为了计算出 bi,首先计算 query 与 key 的「注意力分数」(具体的计算方式可以参考链接,注意力分数,文艺数学君),如下图所示:
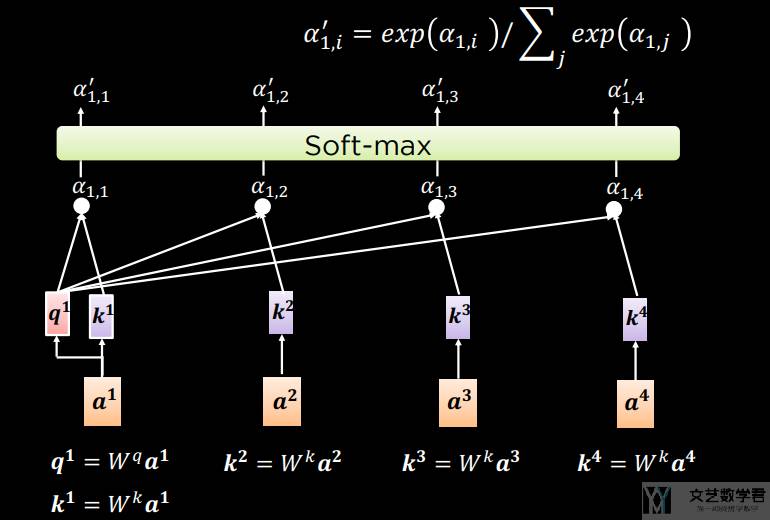
计算出了「注意力分数(attention scores)」之后,我们将「注意力分数」与 value 相乘(相当于是做一个加权平均),最终得到 bi。也就是如下所示的计算过程:
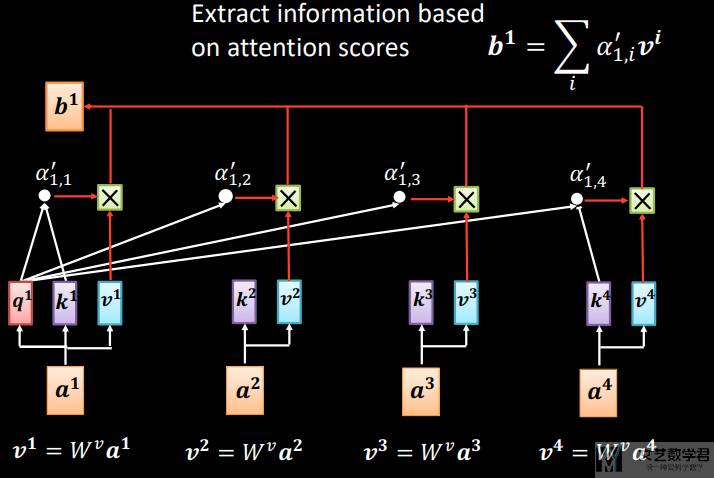
同样的计算方式我们也可以计算 b2,b3,b4。下面再展示一下计算 b2 的计算过程:
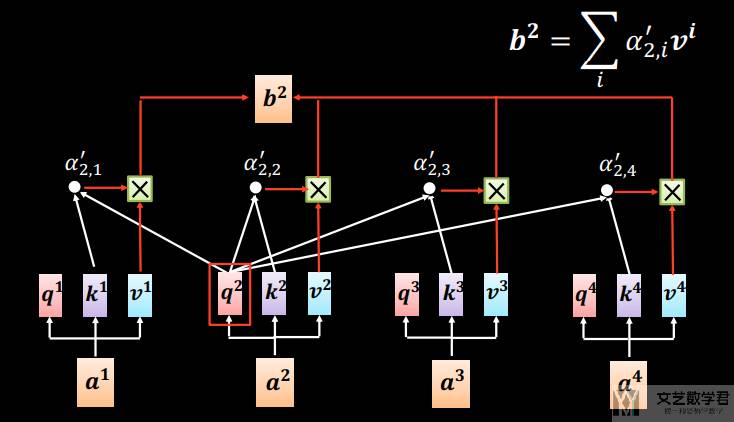
我们可以将「自注意力」看成是一层,也可以一层一层堆加上去,如下图所示:
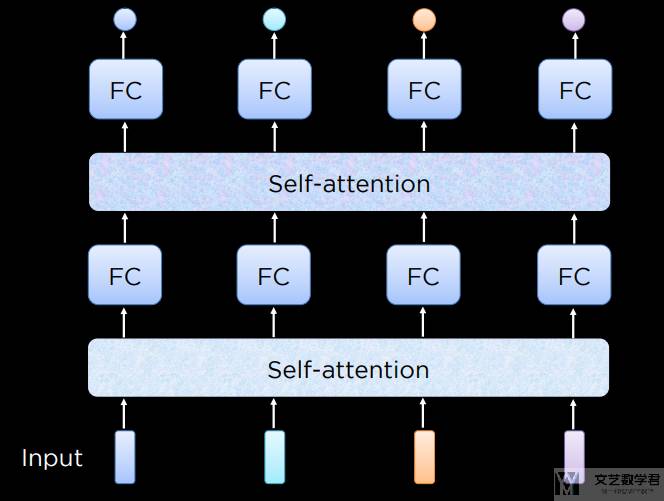
自注意力并行计算
上面我们介绍了分别计算每一个 bi 的方式,其实所有的 bi 是可以并行进行计算的。下面我们使用图示进行简单的说明。首先我们对 query 和 key 和 value 乘系数(在「多头注意力」我们也进行了介绍,乘不同的系数就是「多头注意力」):
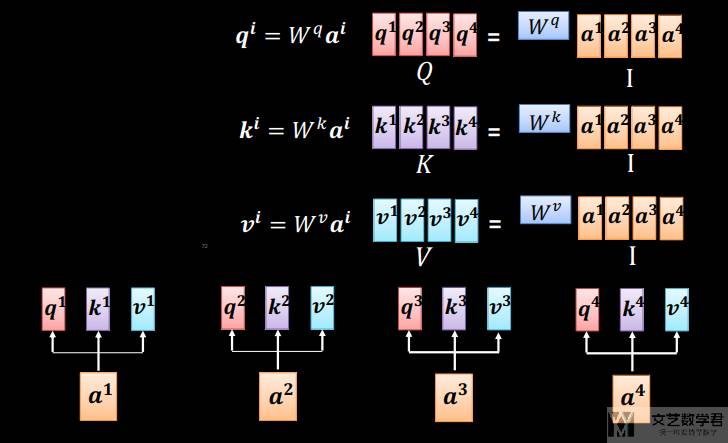
接着我们计算「注意力分数(attention scores)」,如下所示,可以一次性把所有「注意力分数」都算出来:
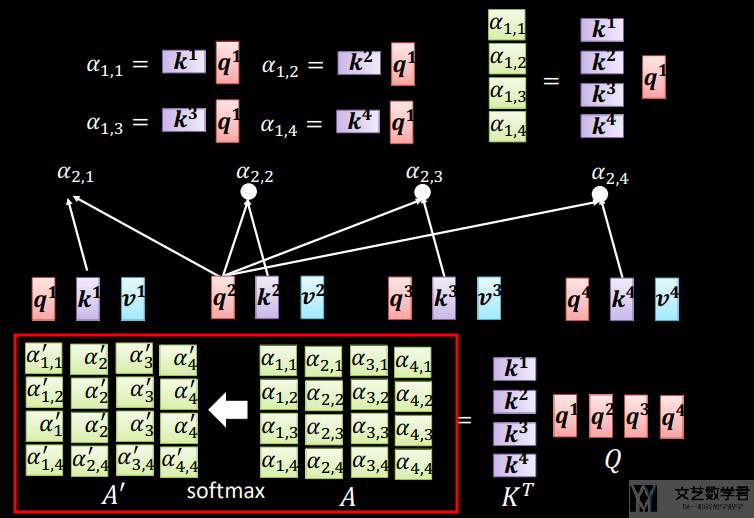
有了「注意力分数(attention scores)」之后,就可以对 value 进行加权求和。下面可以一次性计算出所有的 bi 。
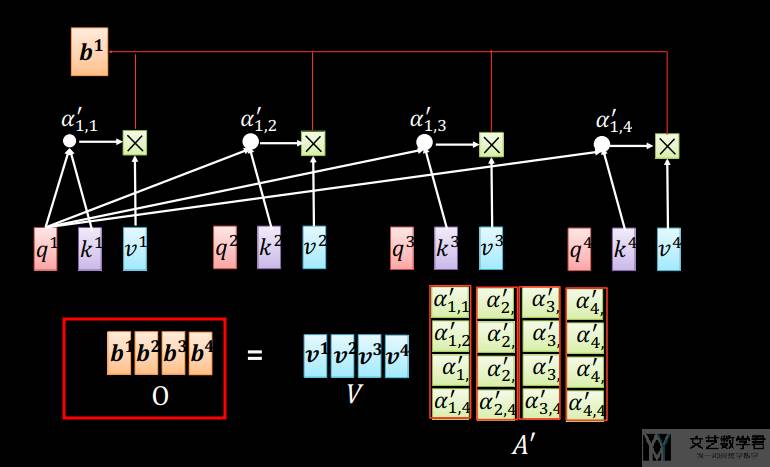
自注意力数学描述
接下来我们再使用数学语言了描述一下「自注意力」。给定一个输入序列 (x1, x2, ..., xn),该序列的自注意力输出为一个长度相同的序列 (y1, y2, ..., yn),其中 y 的计算方式如下(这里我们将上面的 ai 替换为 xi,将 bi 替换为 yi):
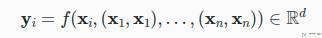
其中 f 为「注意力汇聚函数」。上面式子的含义是,给定 query 为 xi,而 (xi, xi) 又会作为 key-value pair ,然后计算 xi 的注意力输出。需要强调的是,输入有多少个 x,输出就会有多少个 y,他们的个数是一样的。
自注意力代码实现
「自注意力」的代码实现非常简单,就是利用前面的「多头注意力」,唯一不同的就是同样的值,同时作为「查询(query)」、「键(key)」和「值(value)」。
我们可以将其输入和输出的大小完全一模一样,如下所示(注意 attention 里面 X 出现了三次,相当于查询、键和值来自同一组输入):
- # 可以让输入和输出完全一样大小
- num_hiddens = 100 # `qkv` 转换后的大小维度, 单个的维度为 num_hiddens/num_heads
- num_heads = 5 # head 的数量
- attention = MultiHeadAttention(num_hiddens, num_heads, 0.5)
- # 构建输入
- batch_size = 2
- num_queries = 4
- valid_lens = torch.tensor([3, 2])
- X = torch.ones((batch_size, num_queries, num_hiddens))
- print(X.shape)
- attention_result = attention(X, X, X, valid_lens) # q, k, v 都是 x
- # attention 之后的大小 (batch_size, number of queries, num_hiddens)
- print(attention_result.shape)
- """
- torch.Size([2, 4, 100])
- torch.Size([2, 4, 100])
- """
当然我们也可以让其输出的维度不同(当然数量要是相同的)。比如下面的例子,有 4 个 query,每个 query 原始维度为 100,经过 self-attention 之后的维度是 50。
- # 也可以修改输入和输出的大小
- num_hiddens = 50 # `qkv` 转换后的大小维度, 单个的维度为 num_hiddens/num_heads
- num_heads = 5 # head 的数量
- attention = MultiHeadAttention(num_hiddens, num_heads, 0.5)
- batch_size = 2
- num_queries = 4
- valid_lens = torch.tensor([3, 2])
- X = torch.ones((batch_size, num_queries, num_hiddens*2))
- print(X.shape)
- attention_result = attention(X, X, X, valid_lens) # q, k, v 都是 x
- print(attention_result.shape) # attention 之后的大小 (batch_size, number of queries, num_hiddens)
- """
- X, torch.Size([2, 4, 100])
- attention_result, torch.Size([2, 4, 50])
- """
位置编码
在前面介绍的「自注意力」中,我们没有考虑输入的位置信息。换句话说,输入的序列 (x1, x2, ..., xn) 被打乱,对输出的序列 (y1, y2, ..., yn) 值没有影响(顺序会改变,但是值不会改变)。也就是下面的式子,两个式子里面输入序列一个是「正序」,一个是「反序」,最后结果是一样的:
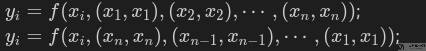
我们可以来验证一下输入的顺序对最终的结果有没有影响。我们构建两个 query,每个 query 的维度是 10。首先我们初始化一个 attention 层:
- # 初始化 attention
- num_hiddens = 10 # `qkv` 转换后的大小维度, 单个的维度为 num_hiddens/num_heads
- num_heads = 5 # head 的数量
- attention = MultiHeadAttention(num_hiddens, num_heads, 0.5)
- attention.eval()
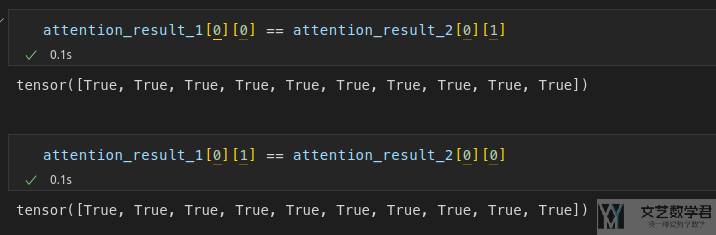
接着分别将 (x1, x2) 和 (x2, x1) 作为模型的输入,得到 attention_result_1(这里相当于是 (y1, y2)) 和 attention_result_2(这里相当于是 (y2, y1))。于是可以验证 attention_result_1[0] 和 attention_result_2[1] 的结果是一样的。实验结果也是证明他们是一样的,如下所示:
位置编码想法
为了解决上面的问题,于是我们提出了位置编码。如下图所示,我们直接将「位置信息」加在原始信息中。
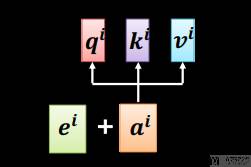
位置编码可以通过学习得到也可以直接固定得到。 接下来,我们描述的是基于正弦函数和余弦函数的固定位置编码。
我们假设输入的数据是一个 n✖m 的矩阵,其中 n 表示一句话有 n 个词,m 表示一个词会转换为长度为 m 的向量。位置编码就是会创建一个一样大的矩阵,也是 n✖m 的矩阵。矩阵中每一个值的计算方式如下所示:
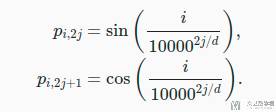
上面的两个式子就是代表矩阵中某一行某一列的值。
- 第
i行,第2j列,对应第一个式子,也就是p_{i, 2j}; - 第
i行,第2j+1列,对应第二个式子,也就是p_{i, 2j+1};
位置编码实现
我们根据上面的式子可以实现出如下的代码。在 init 的时候会生成一个矩阵,矩阵的值和上面式子值的计算方式一样。在 forward 的时候,将 X 和矩阵 P 相加即可。
- class PositionalEncoding(nn.Module):
- """Positional encoding.
- """
- def __init__(self, num_hiddens, dropout, max_len=1000):
- """初始化位置编码的矩阵
- Args:
- num_hiddens (int): 每个字转换为多少维度的特征, 相当于有多少列
- dropout (float): dropout 的比例, 使得 position encoding 更加鲁棒
- max_len (int, optional): 句子的最长的长度, 相当于有多少行. Defaults to 1000.
- """
- super().__init__()
- self.dropout = nn.Dropout(dropout)
- # Create a long enough P
- self.P = torch.zeros((1, max_len, num_hiddens)) # 初始化一个 max_len*num_hiddens 的矩阵 P
- X = torch.arange(max_len, dtype=torch.float32).reshape(-1, 1) # 相当于是 i
- Y = torch.pow(10000, torch.arange(0, num_hiddens, 2, dtype=torch.float32) / num_hiddens) # 10000^(2j/d)
- X = X/Y # i/(10000^(2j/d))
- self.P[:, :, 0::2] = torch.sin(X) # 从 0 开始, 每次间隔 2, 也就是偶数
- self.P[:, :, 1::2] = torch.cos(X) # 从 1 开始, 每次间隔 2, 也就是奇数
- def forward(self, X):
- # 给定 X, 加上 P (位置信息)
- X = X + self.P[:, :X.shape[1], :].to(X.device)
- return self.dropout(X)
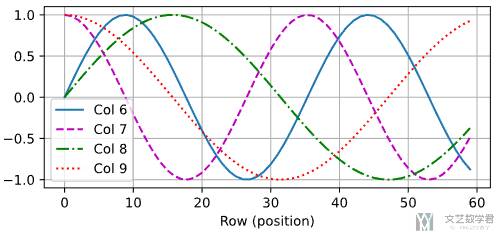
我们将位置编码会值出来。代码如下,可以绘制出不同的双曲函数曲线:
- encoding_dim, num_steps = 32, 60
- pos_encoding = PositionalEncoding(encoding_dim, 0)
- # 输入大小为 (1, 60, 32), 得到的矩阵大小也是一样
- X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
- P = pos_encoding.P[:, :X.shape[1], :] # 只需要与 X 一样的行数
- plot(
- torch.arange(num_steps),
- P[0, :, 6:10].T,
- xlabel='Row (position)',
- figsize=(6, 2.5),
- legend=["Col %d" % d for d in torch.arange(6, 10)]
- )
绘制的结果如下所示。可以看到位置嵌入矩阵的第 6 列和第 7 列的频率高于第 8 列和第 9 列。 第 6 列和第 7 列之间的偏移量(第 8 列和第 9 列相同)是由于正弦函数和余弦函数的交替。
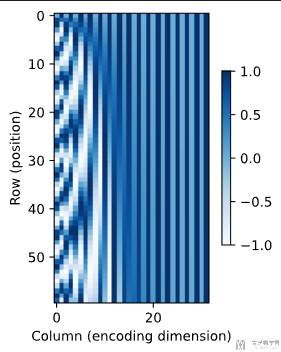
我们也可以使用热力图显示。如下所示,可以看到矩阵中不同位置被加的值不同。且前面的列变化速度会更加快。
相对位置信息
除了捕获绝对位置信息之外,上述的位置编码还允许模型学习得到输入序列中相对位置信息。比如说两个字在句子中的绝对位置可能会发生改变,但是他们的相对位置可能没有改变。
例如现在有两个点的值为 P{i, 2j}, P{i, 2j+1},然后现在变为 P{i+delta, 2j}, P{i_delta, 2j+1}(相当于行的位置变了),那么他们的值可以通过下面的矩阵变换得到:

其中红色框的矩阵没有绝对位置 i。因此我们认为这种位置编码也可以表示相对位置信息。
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-










评论