元胞自动机–康威生命游戏

恩，我又写了一篇关于元胞自动机的，说一下生命游戏吧，懒得打字了，就直接看我的手写体。

我们有了上面的演化的规则，下面我们需要求出规则号，其实有了演化规则你已经可以自己实现了，但是计算出规则号后就可以用mathematica算了，会方便很多。

注意，上面写了四条规则，但是我们只需要看最后会变为存活（即1）这个状态的规则，就是规则2和规则4，下面用手写字体来进行说明。这里外面权重是2，中间权重是1，具体可以看前一篇文章的解释。

那么到这里，我们就已经把规则号计算好了，就是224，接下来就好办了。

把他写成一个函数：

然后，就可以开始使用了：

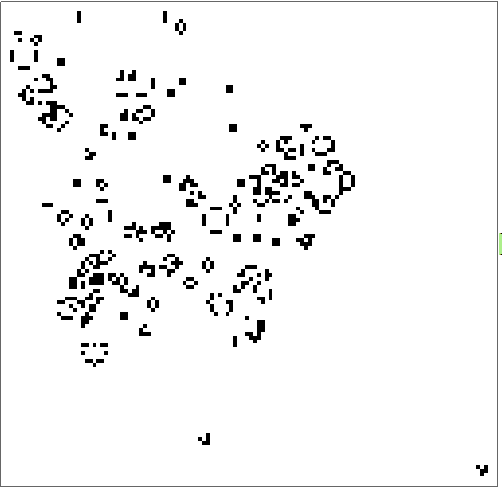
你生成的可能和我这个不一样，因为是随机的

最后看一个动图

那到这里，就把生命游戏讲完了，大家可以自己去玩玩。

最后最后，打个小小的广告，欢迎大家去关注 公众号：文艺数学君（公众号更新比较慢），或者可以收藏本网站呀。