Mathematica画渐近线

之前在看一本习题册的时候看到过关于渐近线的题目，虽然最后求出来了，但是感觉没有图像来得直接，所以这一篇讲一下怎么画出一个函数的渐近线。

当然完全是按照定义去求并画出的。下面我们首先看一下渐近线的定义。

渐近线的定义

三种渐近线：

• 若limf(x)=C,x趋于无穷,则有水平渐近线y=C;
• 若limf(x)=无穷,x趋于x.,则有垂直渐近线x=x.；
• 若limf(x)/x=k不等于0,x趋于无穷,lim(f(x)-kx)=b,x趋于无穷,则有些渐近线y=kx+b.

文字解释

下面用文字再解释一下：

• 水平的就是指当x→∞时,limitf(x)存在,即limitf(x)＝C为某一常数.则y = C 水平渐进线.
• 垂直的就是指当x→C时,y→∞.一般来说,满足分母为0的x,就是所求的渐进线.x = C 就是垂直渐进线；
• 更一般的渐进线，若x→∞时,a ＝ f(x)/x,存在，则再求b ＝ f(x)-ax,(x→∞)，则y = ax + b就是函数的渐进线

Mathematica绘图

有了上面的定义，下面我们就按照定义来画一下函数x+1/x的渐近线。

按照定义，于是我们有下面的代码：

Clear["Global`*"];
f[x_] := x + 1/x;
a = Limit[f[x]/x, x -> Infinity];
b = Limit[f[x] - a*x, x -> Infinity];
Plot[{f[x], a*x + b}, {x, -10, 10}, AspectRatio -> Automatic,PlotRange -> {-7, 7}]

于是，我们画出了下面的图：

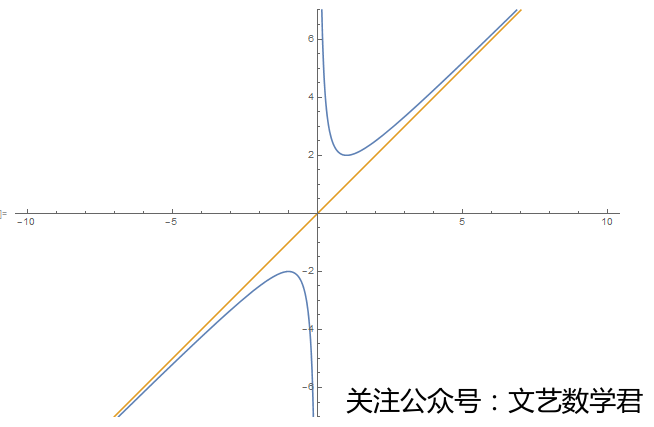
到这里，我们就画出了一个函数的渐近线，其他的也可以根据定义来画出。