这一篇文章会介绍统计中的几大常用分布,以下的代码均是使用mathematica来实现。
文章目录(Table of Contents)
离散分布
二项分布
在进行一项实验时,如果实验可能的结果只有两种,并且每一次实验中产生某一种结果的概率都是相同的,则该试验称为贝努利试验。而二项分布就是n次独立的贝努利试验,各次实验产生的结果相互独立。一般记为b(n,p)。
二项分布的概率分布列:
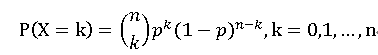
- 均值:np
- 方差:np(1-p)
- 使用mathematica产生二项分布(举例b(100,0.4)):
- dist1 = BinomialDistribution[100, 0.4]
则dist1中存有模拟该二项分布得到的数据
接着我们使用dist1来计算均值和方差:
- Mean[dist1]
- >> 40.
- Variance[dist1]
- >>24. #100*0.4*(1-0.4)
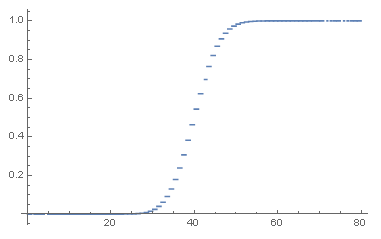
接着画出其分布函数图:
- Plot[CDF[dist1, x], {x, 0, 80}]
画出的图像如下所示:
泊松分布
泊松分布是一种常用的离散分布,它常与单位时间(或单位面积、单位产品等)上的计数过程相联系。X服从参数为λ的泊松分布,记为X~P(λ)。
- 均值:λ
- 方差:λ
- 使用mathematica产生泊松分布(举例P(2)):
- dist2 = PoissonDistribution[2]
则dist2中存有模拟该泊松分布得到的数据
接着我们计算均值和方差,可以看出是和上面方差均值的理论值是相同的:
- Mean[dist2]
- >>2.
- Variance[dist2]
- >>2.
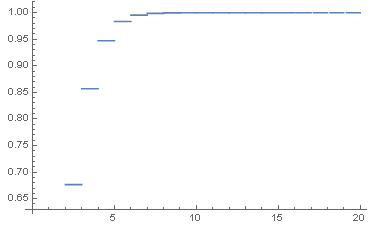
接着我们画出其分布函数图:
- Plot[CDF[dist2, x], {x, 0, 20}]
几何分布
在贝努利试验序列中,记每次实验中事件A发生的概率为p,A出现即为实验成功,X记为A出现为止失败的次数,则X的可能取值为0,1,2,...称X服从几何分布,记为X~Ge(p)。
几何分布的概率分布列:
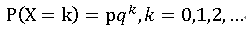
- 均值:q / p
- 方差:q / p^2
接着使用mathematica产生几何分布(举例Ge(0.4)):
- dist3 = GeometricDistribution[0.4]
则dist3中存有模拟该几何分布得到的数据
计算均值和方差:
- Mean[dist3]
- >>1.5.
- Variance[dist3]
- >>3.75.
画出其分布函数图:
- Plot[CDF[dist3, x], {x, 0, 20}]
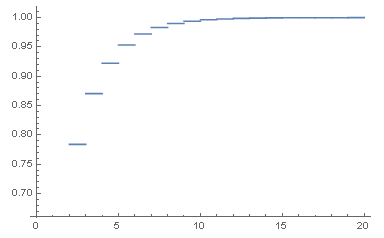
负二项分布
在贝努利试验中,记每次试验中事件A发生的概率为p,记X为事件A出现r次时已经失败的次数,则X服从负二项分布,记为X~Nb(r,p)。
几何分布的概率分布列:
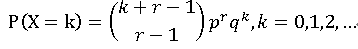
- 均值:rq/p
- 方差:rq/p^2
使用mathematica产生负二项分布(举例Nb(5,0.4)):
- dist4 = NegativeBinomialDistribution[5, 0.4]
则dist4中存有模拟该负二项分布得到的数据
计算均值和方差:
- Mean[dist4]
- 7.5.
- Variance[dist4]
- 18.75.
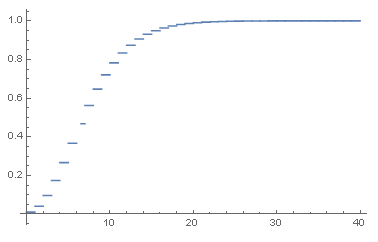
画出其分布函数图:
- Plot[CDF[dist4, x], {x, 0, 40}]
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-











评论