常用连续分布

摘要

随机变量的分布常分为离散分布，连续分布和混合分布，本文主要介绍在概率论与数理统计中常用的几大连续分布，以及如何使用 Mathematica 调用使用相应分布并画图。

连续分布

这里介绍一些常用的连续分布，关于使用 matplotlib 可视化分布的 pdf（概率密度函数） 和 cdf（累计分布函数），可以参考文章，matplotlib 可视化概率密度函数(pdf)和累计分布函数(cdf)

这一章中所有的测试均使用 mathematicas 来进行测试，例如绘制 cdf 和 pdf，计算均值与方差。

正态分布

• 正态分布（Normal distribution），又名高斯分布（Gaussian distribution）,若随机变量 X 服从一个数学期望为 μ、方差为 σ^2 的正态分布，记为 X~N(μ， σ^2)。
• 正态分布的概率分布列：

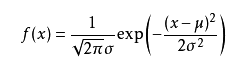
• 均值：μ
• 方差：σ^2
• 使用 mathematica 产生正态分布（举例 N(0,1)）：

则 data1中存有模拟该正态分布得到的数据

• 计算均值和方差：

•  画出正态分布的概率密度函数图（pdf）：

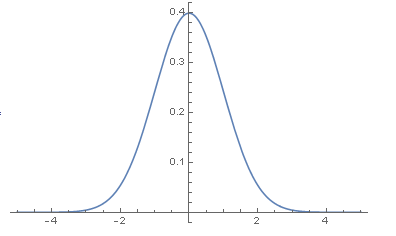
• 可视化正态分布的分布函数图（cdf）：

 

均匀分布

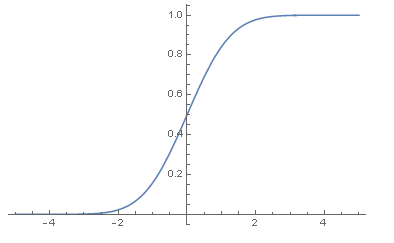
• 在概率论和统计学中，均匀分布也叫矩形分布，它在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数 a 和 b 定义，它们是数轴上的最小值和最大值，通常记为 U(a, b)。
• 均匀分布的概率分布列：

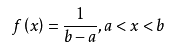
• 均值： (a+b)/2
• 方差：(b-a)^2/12
• 使用 mathematica 产生均匀分，举例 U(0,1)：

则 data2 中存有模拟该均匀分布得到的数据，下面计算均匀分布的均值方差，并绘制出 pdf 和 cdf。

• 计算均值和方差：

•  画出其密度函数图：

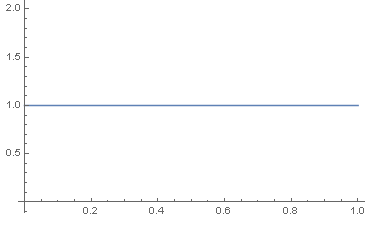
• 画出其分布函数图：

 

指数分布

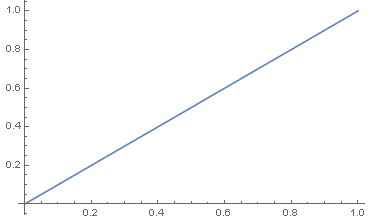
• 指数分布，也称为负指数分布，具有无记忆的性质，其中 λ > 0 是分布的一个参数， 如果一个随机变量 X 呈指数分布，则可以记作 X~Exp(λ)。
• 指数分布的概率分布列：

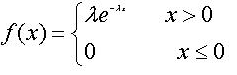
均值：1/λ

方差：1/λ^2

使用 mathematica 产生指数分布，这里举例 Exp(0.5)：

则data3中存有模拟该指数分布得到的数据

• 计算均值和方差：

• 画出其密度函数图：

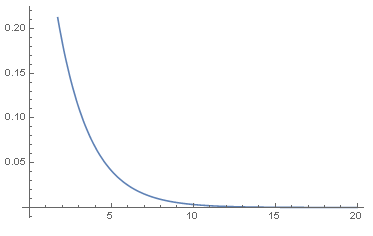
• 画出其分布函数图：

 

伽马分布

• 伽玛分布（Gamma Distribution）中的参数 α 称为形状参数，β 称为尺度参数，若随机变量服从伽马分布，则记为 X~Ga(α，β)。
• 伽马分布的概率分布列：

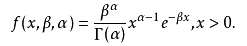
均值：α/β

方差：α/β^2

使用 mathematica 产生伽马分布，举例 Ga(2，2)：

则 data4 中存有模拟该伽马分布得到的数据

• 计算均值和方差：

• 画出其密度函数图：

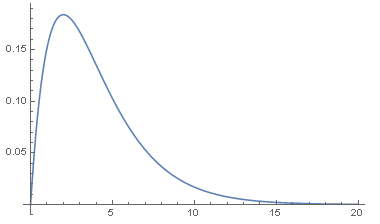
• 画出其分布函数图：

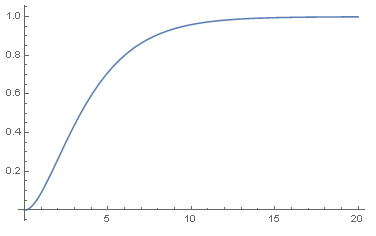
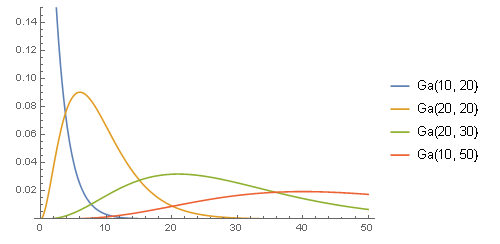
• 不同参数的密度函数比较：

 

贝塔分布

• 服从贝塔分布（Beta Distribution)的变量 x 仅能出现于 0 到 1 之间，a，b是两个大于 0 的参数，随机变量服从参数为 a 和 b 的贝塔分布，则记为 X~B(a,b)。
• 伽马分布的概率分布列：

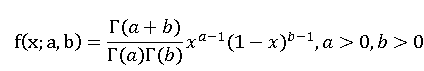
• 均值：a/(a+b)
• 方差：ab / ((a+b)^2*(a+b+1))
• 使用 Mathematica 产生伽马分布，举例Be(2，2)：

则 data5 中存有模拟该贝塔分布得到的数据

• 计算均值和方差：

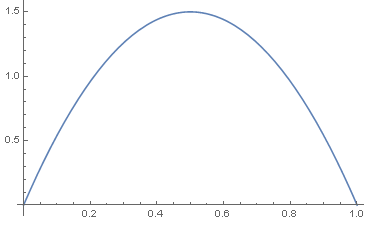
• 画出其密度函数图：

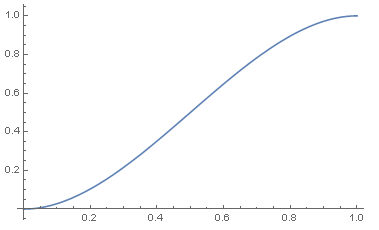
• 画出其分布函数图：

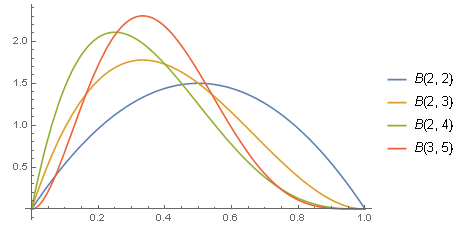
• 不同参数的密度函数比较：