应用回归分析之简单线性回归(SPSS版本)

例题解析

为研究某一大都市报开设周日版的可行性，获得了34种报纸的平日和周日的发行量信息（以千为单位）。数据如下：

 

{Daily,Sunday}: {391.95, 488.51}, {516.98, 798.3}, {355.63, 235.08}, {238.55, 299.45}, {537.78, 559.09}, {733.78, 1133.25}, {198.83, 348.74}, {252.62, 417.78}, {206.2, 344.52}, {231.18, 323.08}, {449.76, 620.75}, {288.57, 423.3}, {185.74, 202.61}, {1164.39, 1531.53}, {444.58, 553.48}, {412.87, 685.97}, {272.28, 324.24}, {781.8, 983.24}, {1209.22, 1762.02}, {825.51, 960.31}, {223.75, 284.61}, {354.84, 407.76}, {515.52, 982.66}, {220.46, 557.}, {337.67, 440.92}, {197.12, 268.06}, {133.24, 262.05}, {374.01, 432.5}, {273.84, 338.36}, {570.36, 704.32}, {391.29, 585.68}, {201.86, 267.78}, {321.63, 408.34}, {838.9, 1165.57}

 

SPSS

==1.计算协方差与相关系数==

• 将数据导入SPSS

• 方法：

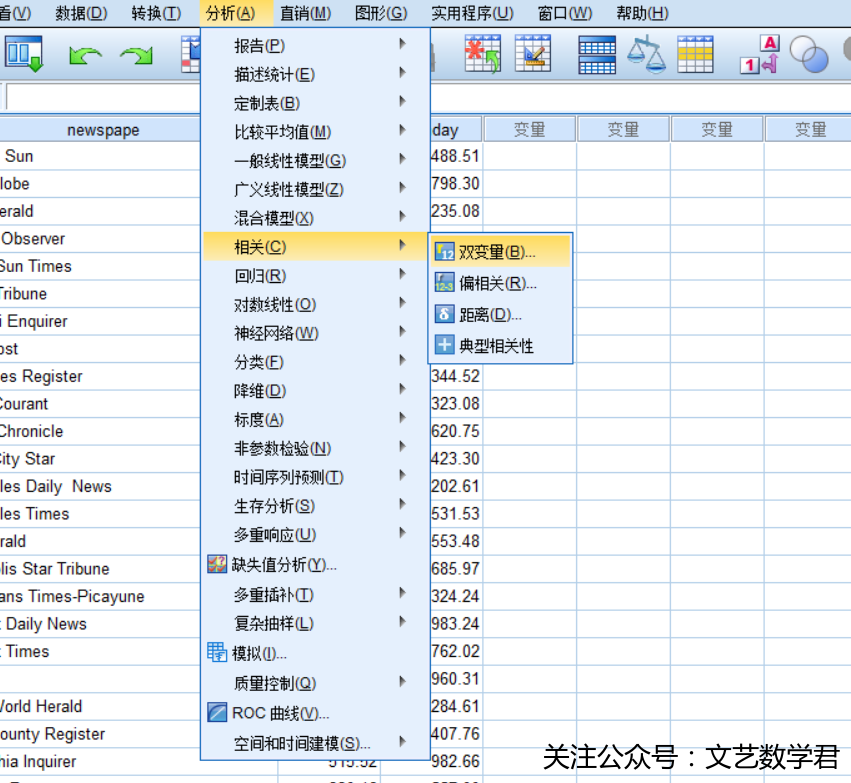
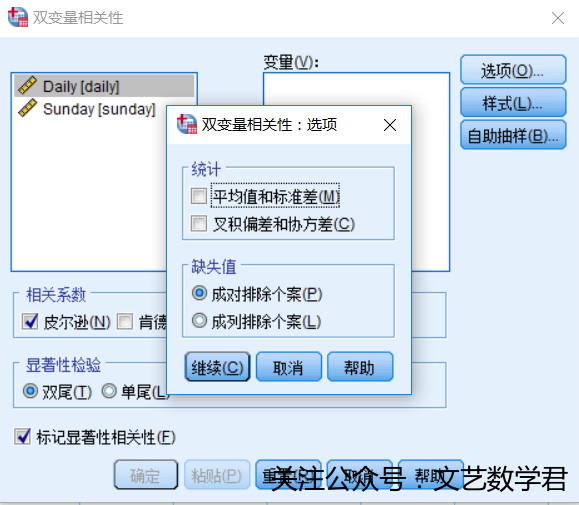
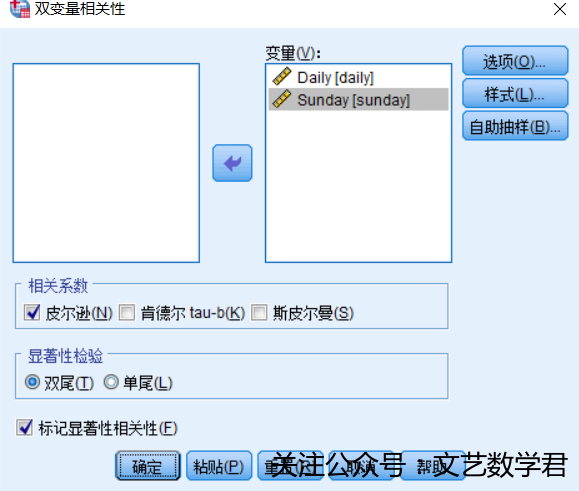
• 结果：

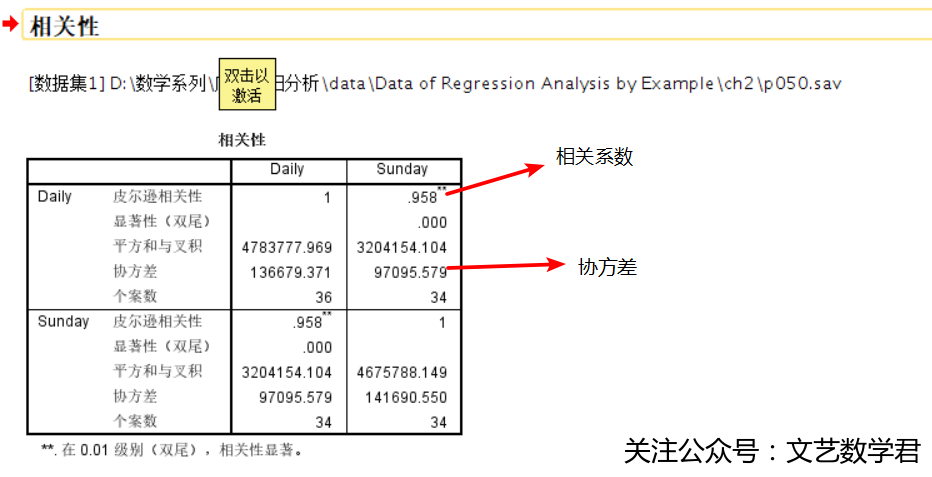
==2.构造散点图==

• 方法：

• 结果：

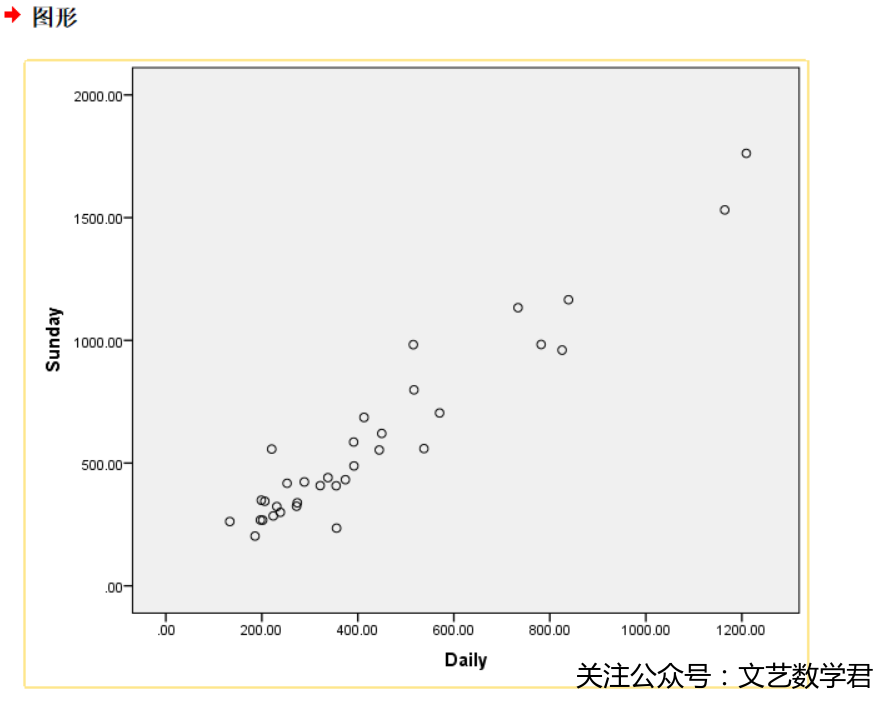
==3.拟合回归直线==

• 方法：

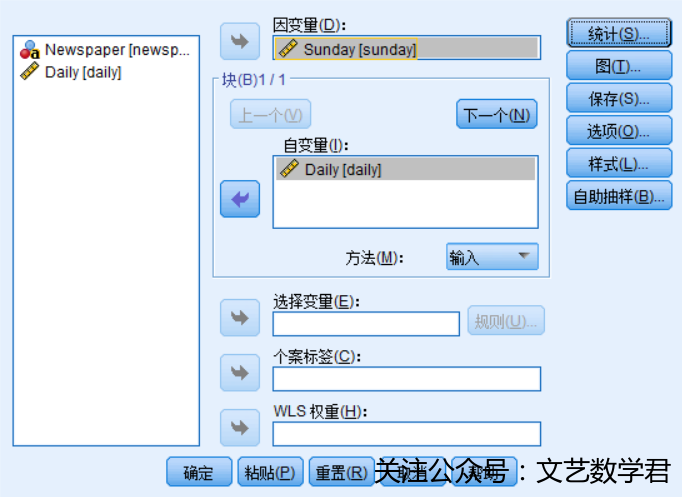
• 结果：

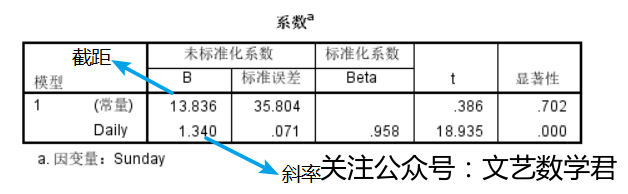
==4.计算回归直线参数的95%置信区间==

• 方法：

• 结果：

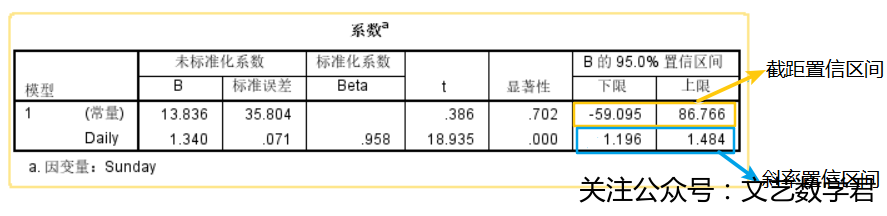
==5.当平日发行量为500000时，给出报纸周日发行量均值的95%置信区间==

==6.某一正在考虑提供周日版的报纸，平日发行量为500000.给出该报纸周日发行量的95%预测区间==

5，6题的解答下面一起给出

• 方法：将500000统一单位后（500千）加入数据表格，然后如图操作：

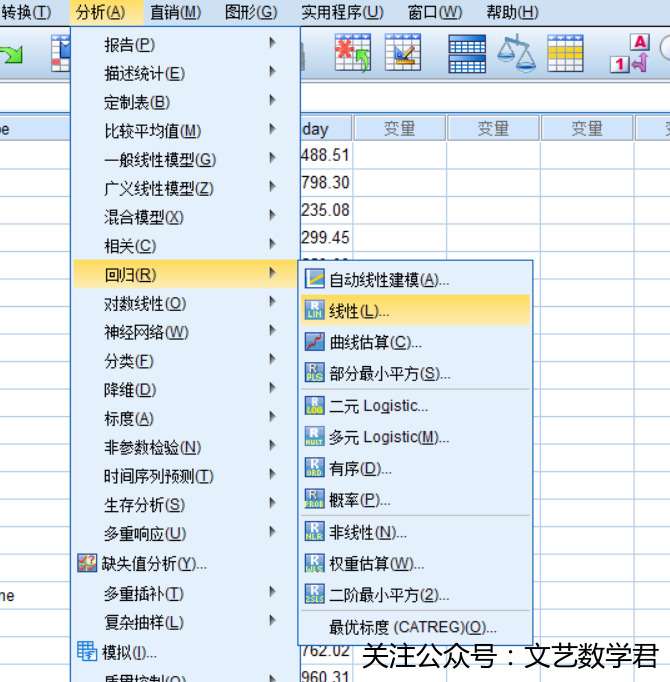
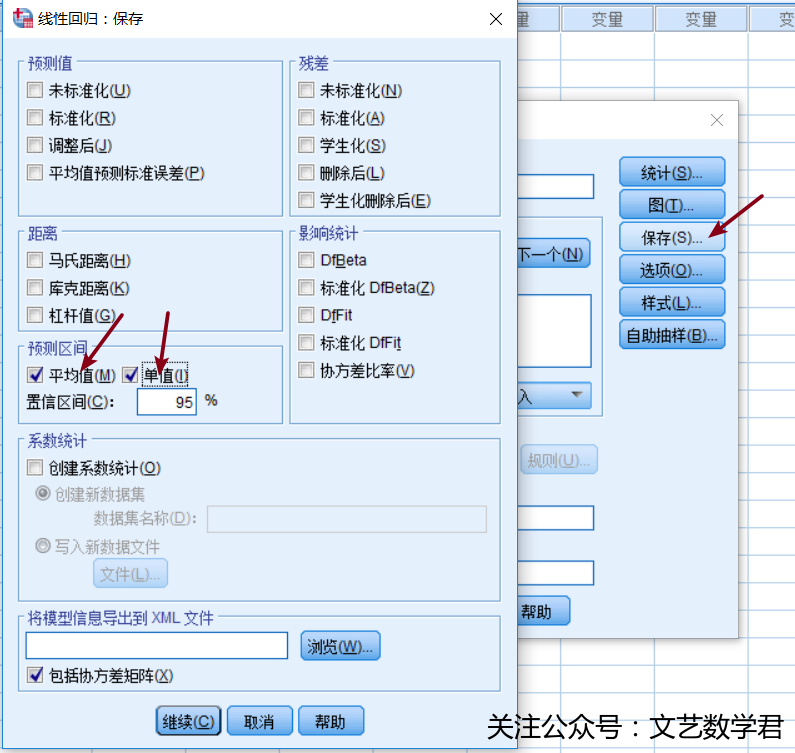
• 结果：