应用回归分析之简单线性回归(Mathematica版本)

摘要

这一篇文章会主要研究在应用回归分析中线性回归的一些使用，我们在这里会通过具体的例子，使用spss和Mathematica分别来做示范，也可以算是Wolfram语言与数学了。 这篇文章主要涉及到的知识点–画散点图，拟合直线，求参数的置信区间，并给出预测的值

 

例题解析

 

为研究某一大都市报开设周日版的可行性，获得了34种报纸的平日和周日的发行量信息（以千为单位）。数据如下：

 

{Daily,Sunday}: {391.95, 488.51}, {516.98, 798.3}, {355.63, 235.08}, {238.55, 299.45}, {537.78, 559.09}, {733.78, 1133.25}, {198.83, 348.74}, {252.62, 417.78}, {206.2, 344.52}, {231.18, 323.08}, {449.76, 620.75}, {288.57, 423.3}, {185.74, 202.61}, {1164.39, 1531.53}, {444.58, 553.48}, {412.87, 685.97}, {272.28, 324.24}, {781.8, 983.24}, {1209.22, 1762.02}, {825.51, 960.31}, {223.75, 284.61}, {354.84, 407.76}, {515.52, 982.66}, {220.46, 557.}, {337.67, 440.92}, {197.12, 268.06}, {133.24, 262.05}, {374.01, 432.5}, {273.84, 338.36}, {570.36, 704.32}, {391.29, 585.68}, {201.86, 267.78}, {321.63, 408.34}, {838.9, 1165.57}

 

之前会有一个spss版本的应用回归分析之简单线性回归：https://mathpretty.com/8548.html，  大家可以先看spss版本的带有图形化界面的，再熟悉使用mathematica来操作。

 

下面开始讲如何使用mathematica来做简单的线性回归。

 

==1.计算协方差与相关系数==

• 将数据导入Mathematica

 

a = Import["D:\\作业一\\工作簿3.xlsx"]

a1 = a[[1]]

 

• 计算协方差

方法：

 

a2 = Table[{a1[[i]][[1]]}, {i, 1, Length[a1] - 2}]

a3 = Table[{a1[[i]][[2]]}, {i, 1, Length[a1] - 2}]

N[Covariance[a2, a3]]

 

结果：

 

{{97095.9}}

 

• 计算相关系数

方法：

 

N[Correlation[a2, a3]]

 

 

结果：

 

{{0.958154}}

 

 

==2.构造散点图==

• 方法：

 

ListPlot[a1]

 

 

• 结果：

 

 

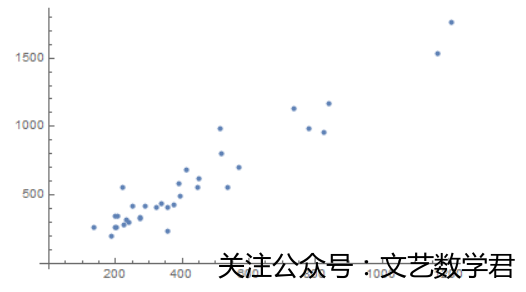
==3.拟合回归直线==

• 方法：

 

lm = LinearModelFit[a4, x, x]

Normal[lm]

 

 

• 结果：

 

13.834 + 1.33972 x

 

 

==4.计算回归直线参数的95%置信区间==

• 方法：

 

lm["ParameterConfidenceIntervals"]

 

 

• 结果：

 

{{-59.0972, 86.7651}, {1.1956, 1.48384}}

 

 

==5.当平日发行量为500000时，给出报纸周日发行量均值的95%置信区间==

• 方法：

 

(*计算残差*)

e = Sum[(a3[[i]] - 13.834 - 1.33972*a2[[i]])^2, {i, 1, Length[a1] - 2}]

sigma = (e/32)^(1/2)

mu = Mean[a2]

(*计算日发行量500千的时候周日发行量的预测*)

y0 = 13.834 + 1.33972*500

Needs["HypothesisTesting`"]

(*三个参数为均值，方差，自由度*)

StudentTCI[y0,sigma*(1 + 1/34 + (500 - mu)^2/(33*Variance[a2]))^(1/2), 32]

 

 

• 结果：

 

{{457.335}, {910.053}}

 

 

==6.某一正在考虑提供周日版的报纸，平日发行量为500000.给出该报纸周日发行量的95%预测区间==

• 方法：

 

Needs["HypothesisTesting`"]

(*三个参数为均值，方差，自由度*)

StudentTCI[y0, sigma*(1/34 + (500 - mu)^2/(33*Variance[a2]))^(1/2), 32]

 

 

• 结果：

 

{{644.196}, {723.192}}