应用回归分析之多元线性回归（SPSS版本）

例题解析|香烟消费模式的研究

主要研究内容

这一篇文章会主要研究在应用回归分析中多元线性回归的一些使用，我们在这里会通过具体的例子，使用spss和Mathematica分别来做示范，也可以算是Wolfram语言与数学了。

这篇文章主要涉及到的知识点--多元回归分析，假设检验，拟合优度

欢迎大家关注文艺数学君的公众号，（二维码在文章最下面）

应用回归分析之前的文章：

应用回归分析之简单线性回归(Mathematica版本)

应用回归分析之简单线性回归(SPSS版本)

香烟消费数据：一个国家的保险组织希望研究50个州和哥伦比亚特区的香烟消费模式。这一研究中选择的变量数据如下：

{age, hs, income, black, female, price, sales}:
{{27., 41.3, 2948., 26.2, 51.7, 42.7, 89.8}, {22.9, 66.7, 4644., 3., 45.7, 41.8, 121.3}, {26.3, 58.1, 3665., 3., 50.8, 38.5, 115.2}, {29.1, 39.9, 2878., 18.3, 51.5, 38.8, 100.3}, {28.1, 62.6, 4493., 7., 50.8, 39.7, 123.}, {26.2, 63.9, 3855., 3., 50.7, 31.1, 124.8}, {29.1, 56., 4917., 6., 51.5, 45.5, 120.}, {26.8, 54.6, 4524., 14.3, 51.3, 41.3, 155.}, {28.4, 55.2, 5079., 71.1, 53.5, 32.6, 200.4}, {32.3, 52.6, 3738., 15.3, 51.8, 43.8, 123.6}, {25.9, 40.6, 3354., 25.9, 51.4, 35.8, 109.9}, {25., 61.9, 4623., 1., 48., 36.7, 82.1}, {26.4, 59.5, 3290., 0.3, 50.1, 33.6, 102.4}, {28.6, 52.6, 4507., 12.8, 51.5, 41.4, 124.8}, {27.2, 52.9, 3772., 6.9, 51.3, 32.2, 134.6}, {28.8, 59., 3751., 1.2, 51.4, 38.5, 108.5}, {28.7, 59.9, 3853., 4.8, 51., 38.9, 114.}, {27.5, 38.5, 3112., 7.2, 50.9, 30.1, 155.8}, {24.8, 42.2, 3090., 29.8, 51.4, 39.3, 115.9}, {28., 54.7, 3302., 0.3, 51.3, 38.8, 128.5}, {27.1, 52.3, 4309., 17.8, 51.1, 34.2, 123.5}, {29., 58.5, 4340., 3.1, 52.2, 41., 124.3}, {26.3, 52.8, 4180., 11.2, 51., 39.2, 128.6}, {26.8, 57.6, 3859., 0.9, 51., 40.1, 104.3}, {25.1, 41., 2626., 36.8, 51.6, 37.5, 93.4}, {29.4, 48.8, 3781., 10.3, 51.8, 36.8, 121.3}, {27.1, 59.2, 3500., 0.3, 50., 34.7, 111.2}, {28.6, 59.3, 3789., 2.7, 51.2, 34.7, 108.1}, {27.8, 65.2, 4563., 5.7, 49.3, 44., 189.5}, {28., 57.6, 3737., 0.3, 51.1, 34.1, 265.7}, {30.1, 52.5, 4701., 10.8, 51.6, 41.7, 120.7}, {23.9, 55.2, 3077., 1.9, 50.7, 41.7, 90.}, {30.3, 52.7, 4712., 11.9, 52.2, 41.7, 119.}, {26.5, 38.5, 3252., 22.2, 51., 29.4, 172.4}, {26.4, 50.3, 3086., 0.4, 49.5, 38.9, 93.8}, {27.7, 53.2, 4020., 9.1, 51.5, 38.1, 121.6}, {29.4, 51.6, 3387., 6.7, 51.3, 39.8, 108.4}, {29., 60., 3719., 1.3, 51., 29., 157.}, {30.7, 50.2, 3971., 8., 52., 44.7, 107.3}, {29.2, 46.4, 3959., 2.7, 50.9, 40.2, 123.9}, {24.8, 37.8, 2990., 30.5, 50.9, 34.3, 103.6}, {27.4, 53.3, 3123., 0.3, 50.3, 38.5, 92.7}, {28.1, 41.8, 3119., 15.8, 51.6, 41.6, 99.8}, {26.4, 47.4, 3606., 12.5, 51., 42., 106.4}, {23.1, 67.3, 3227., 0.6, 50.6, 36.6, 65.5}, {26.8, 57.1, 3468., 0.2, 51.1, 39.5, 122.6}, {26.8, 47.8, 3712., 18.5, 50.6, 30.2, 124.3}, {27.5, 63.5, 4053., 2.1, 50.3, 40.3, 96.7}, {30., 41.6, 3061., 3.9, 51.6, 41.6, 114.5}, {27.2, 54.5, 3812., 2.9, 50.9, 40.2, 106.4}, {27.2, 62.9, 3815., 0.8, 50., 34.4, 132.2}}

SPSS

==1.检验在销量关于6个预测变量的线性回归模型中，女性比例这一变量是不必要的==

• 将数据导入SPSS

• 方法：

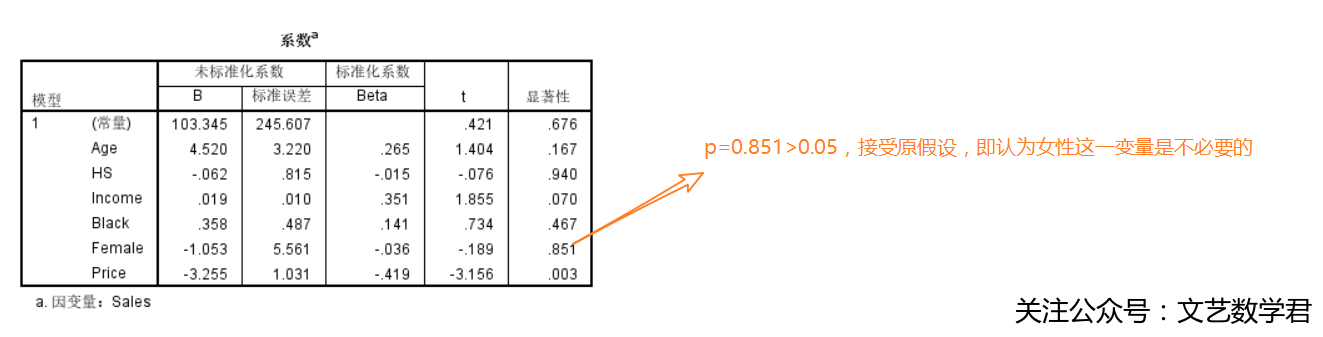
• 结果：

如图所示，零假设Female的系数是0的p值是0.851，无论取0.05还是0.1的显著性检验水平，都比0.851小，所以我们不应该拒绝Female的系数是零的假设，意味着在销量关于6个预测变量的线性回归模型中，女性比例这一变量是不必要的。

==2.检验上述回归方程中女性比例和HS这两个变量都不必要==

• 理论方法及结果：

• 我们把Age设为X1，把HS设为X2，把Income设为X3，把Black设为X4，把Female设为X5，把Price设为X6
• 我们假设检验：

RM: H0: β0+β1X1+β3X3+β4X4+ε| β2,β5=0
FM: H1: β0+β1X1+β2X2+β3X3+β4X4+β5X5+β6X6+ε

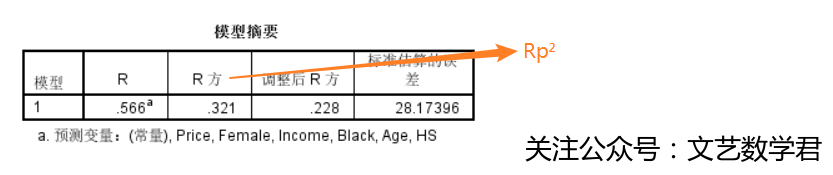
我们假设Rq为H0的拟合优度，Rp为H1的拟合优度 我们构造检验量: F=[(Rp^2^-Rq^2^)/(6-4)]/[(1-Rp^2^)/(51-6-1)] 符合F(2,44)分布

• 表中可以查到，Rp=0.321，Rq=0.320

所以F≈0.0324 而我们查表可得F(2,44;0.05)>F(2,60;0.05)=3.15 所以F< F(2,44;0.05) 所以我们不应该拒绝H0，也就是说上述回归方程中女性比例和HS这两个变量都不必要。

• 实践方法：

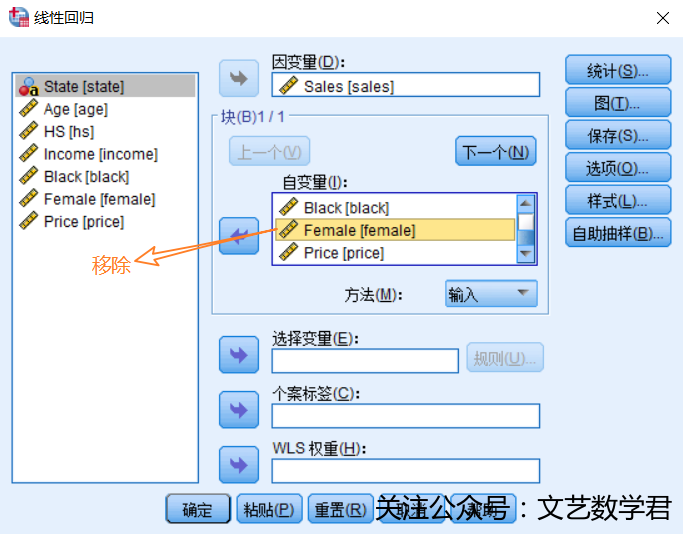
==3.当收入变量从上述回归模型中去除时，销量变量可以被其他预测变量解释的百分比是多少？==

• 方法： 我们将Y视为相应变量，将X1，X2，X4，X5，X6视为解释变量，建立回归模型，并从所得表格中提取拟合优度：

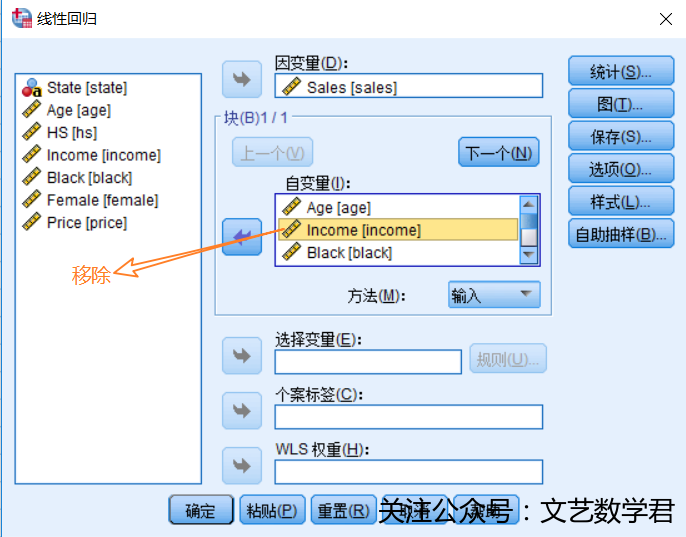
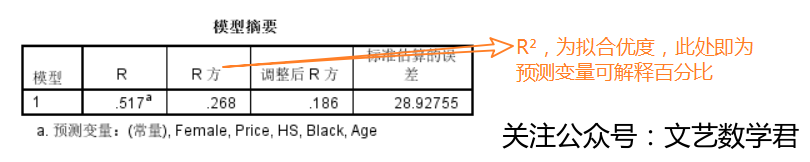
• 结果：

我们可以看到拟合优度R^2^为0.268，即当收入变量从上述回归模型中去除时，销量变量可以被其他预测变量解释的百分比是26.8%

到这里就讲完了关于使用spss来进行多元分析的例子了。