应用回归分析案例–NBA选秀数据分析

这一篇文章我们会使用之前学习的回归分析的知识来做一个真实数据的分析，也是在应用中学习吧。下面我们就开始吧。

背景

NBA选秀（NBA Draft）为一年一度的NBA挑选新球员的盛会。在选秀大会上，30支NBA球队都可以挑选想加入NBA的年轻男性球员，被选中的球员则被称为NBA新秀。

每年在新人们正式参加NBA选秀前，NBA都会举办体能测试训练营来对新人们的身体素质进行衡量和评估。体测全称身体素质测试，在NBA是对球员进行考察及能力评估的重要手段，分为静态体测和动态体测两大项，静态体测包括身高，穿鞋身高，体重，臂展，8次以上的卧推，手掌大小以及站立摸高；动态体测包括纵跳高度，助跑摸高，折返跑速度，3/4场地冲刺，侧向移动速度以及半场定点跑位速度。体测数据是考察球员能力.身体素质.潜力的重要手段. 让球队更直接的了解球员情况的数据。

这项体测不是强制性的，是否参与或者只参与其中几项完全由新秀自行决定，所以会导致很多人的身体数据并不完全，这在一定程度上会影响人们对该球员身体素质的评估以及选秀夜30支NBA球队的选择。

在本例中我们一方面希望能够找出各部分变量间可能存在的关系，另一方面希望能够在其中筛选出具有代表性的体测变量，即仅用一个或几个体测变量的数据便能衡量该球员的整体身体情况如何。

分析

我们找寻了2013、2015、2016这三年的新秀体测数据来进行分析。数据存在缺失，目前我们无法利用现有数据进行补充，不过在我们找到变量间的关系后可以利用模型对部分缺失数据做出一定程度上合理的预测。

一、寻找变量间的关系（以身高—臂展为例）

• 在删除掉身高臂展中存在缺失的数据后，我们利用SPSS绘制了身高与臂展的散点图，

散点图可以帮助我们更好的观察两个变量间可能存在的关系。

• 具体实现步骤如下：

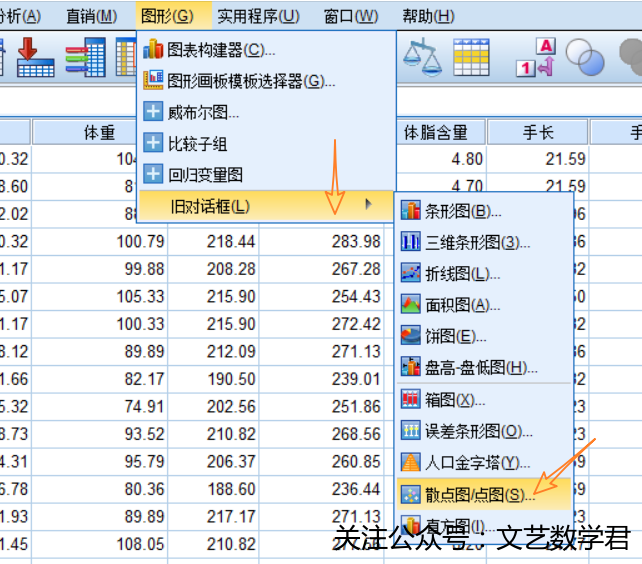
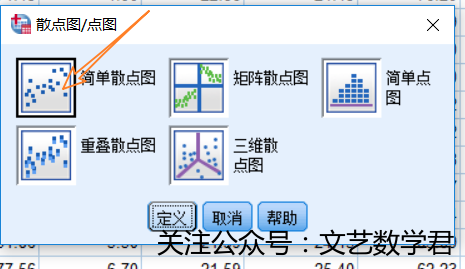
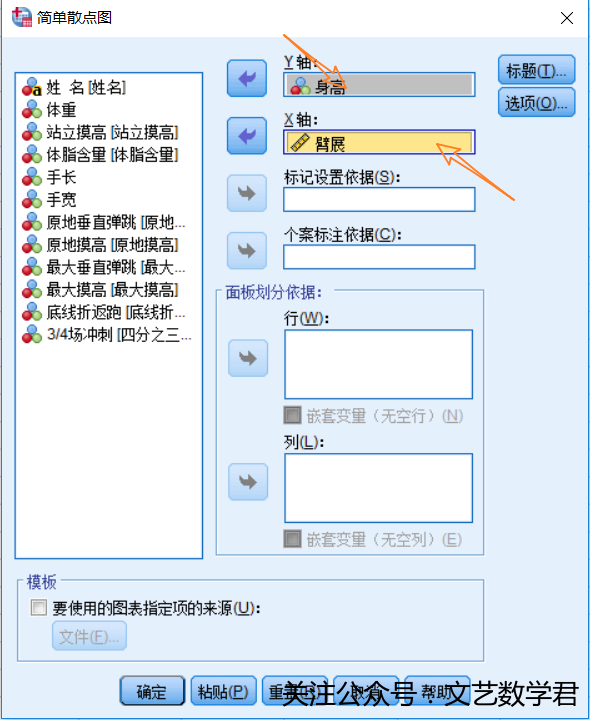
• 得到散点图如下：

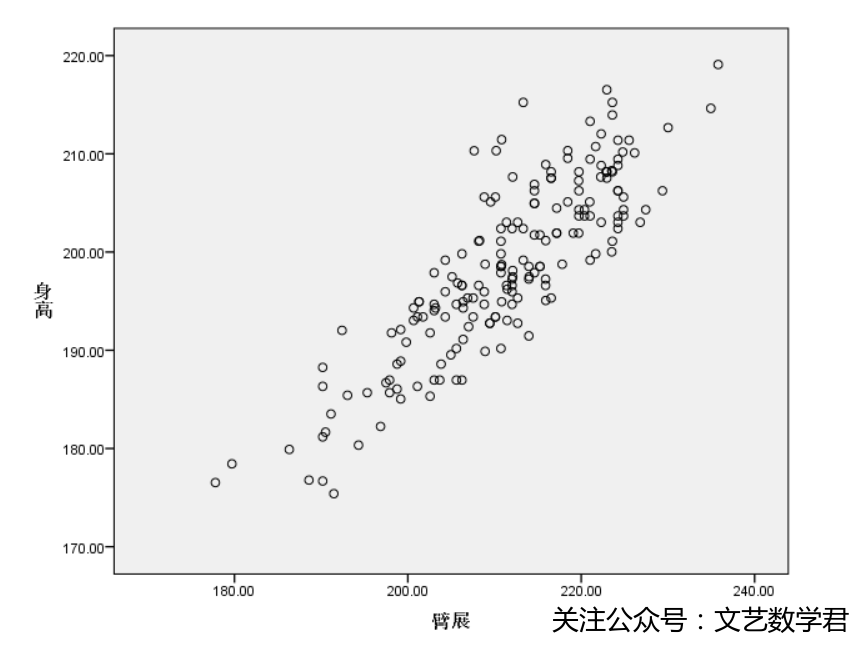
可以看到这些点大致分布在一条直线附近，这说明身高与臂展间存在较强的线性关系。为进一步说明问题，我们计算了身高与臂展的相关系数，这里先说明一下相关系数的数学原理（关于相关系数的更多知识，可以查看之前写的文章，应用回归分析之简单线性回归(SPSS版本)）：

相关系数的解释

相关系数是衡量两个变量间的线性关系强弱的统计量，相关系数为正，说明两个变量呈正相关；相关系数为负，说明两个变量呈负相关。且相关系数绝对值越大，说明两个变量间的线性关系越强。

两个变量X、Y的相关系数计算公式为：Corr(X,Y)=(Cov(X,Y))/(√(Var(X)) √(Var(Y)))，其中，Cov(X,Y)为两个变量间的协方差，Var(X),Var(Y)分别为两个变量的方差。

• 利用SPSS计算两个变量的相关系数方法如下：

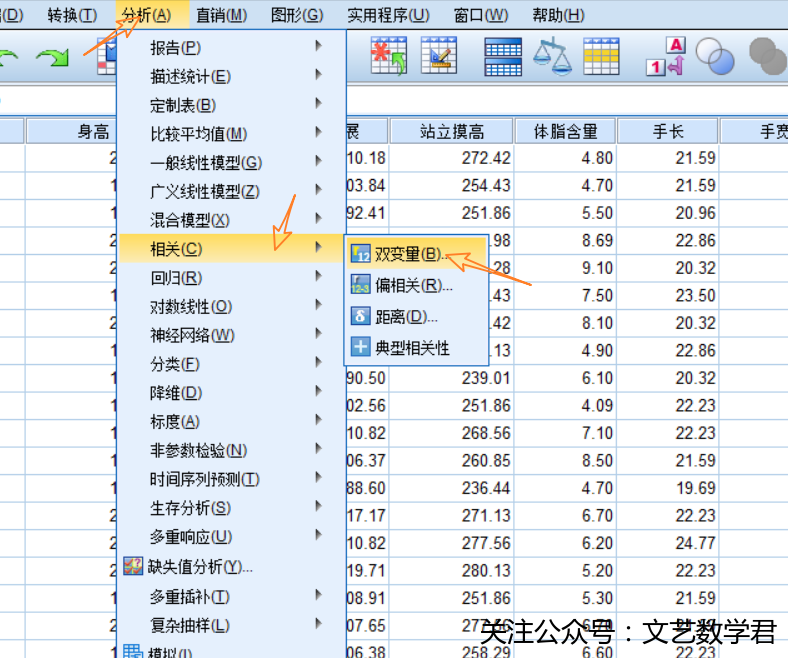
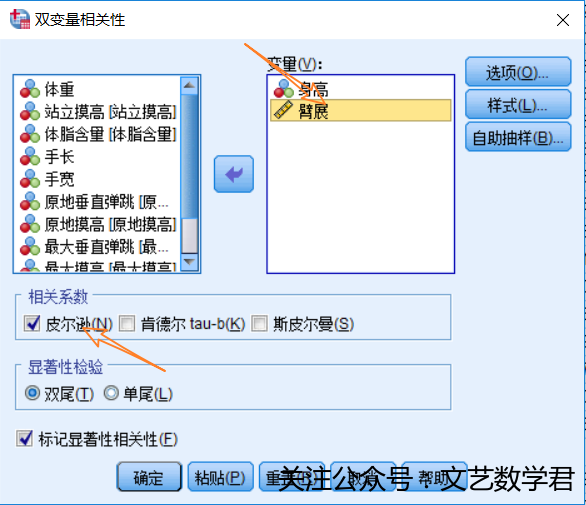
• 得到结果如下：

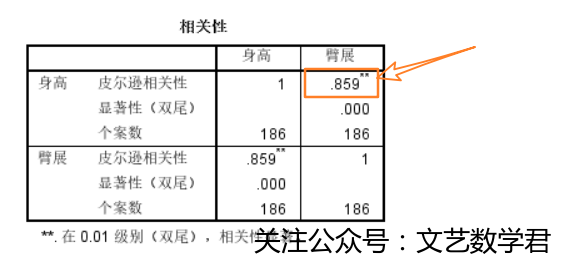
• 可以看到身高与臂展的相关系数达到了0.859，一般我们认为相关系数超过0.75就有较强的线性相关性，这里可以认为身高与臂展间存在很强的线性关系。

• 接下来我们进行线性模型拟合，通常我们所用的线性模型拟合方法是最小二乘法，这里先对最小二乘法的数学原理做一个介绍：

最小二乘法

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：

（1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。

（2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。

（3）最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。这种方法对异常值非常敏感。

最常用的是普通最小二乘法（ Ordinary Least Square，OLS）：所选择的回归模型应该使所有观察值的残差平方和达到最小。（Q为残差平方和）- 即采用平方损失函数。

• 具体操作如下：

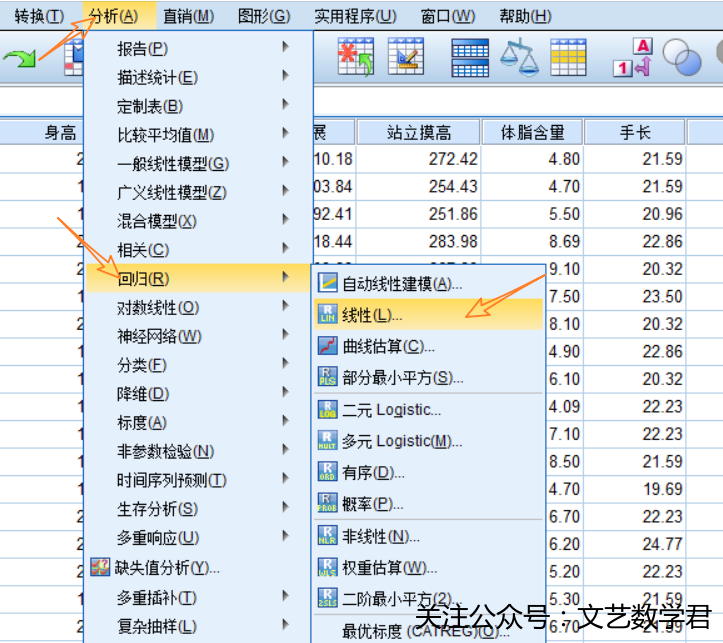
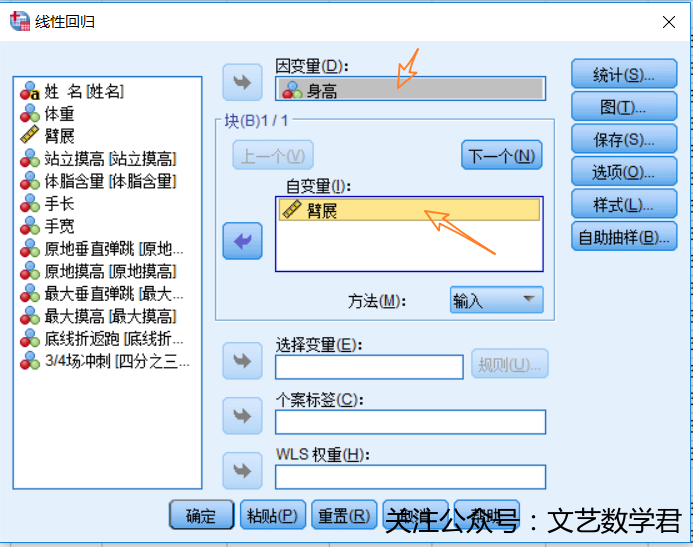
• 得到结果如下：

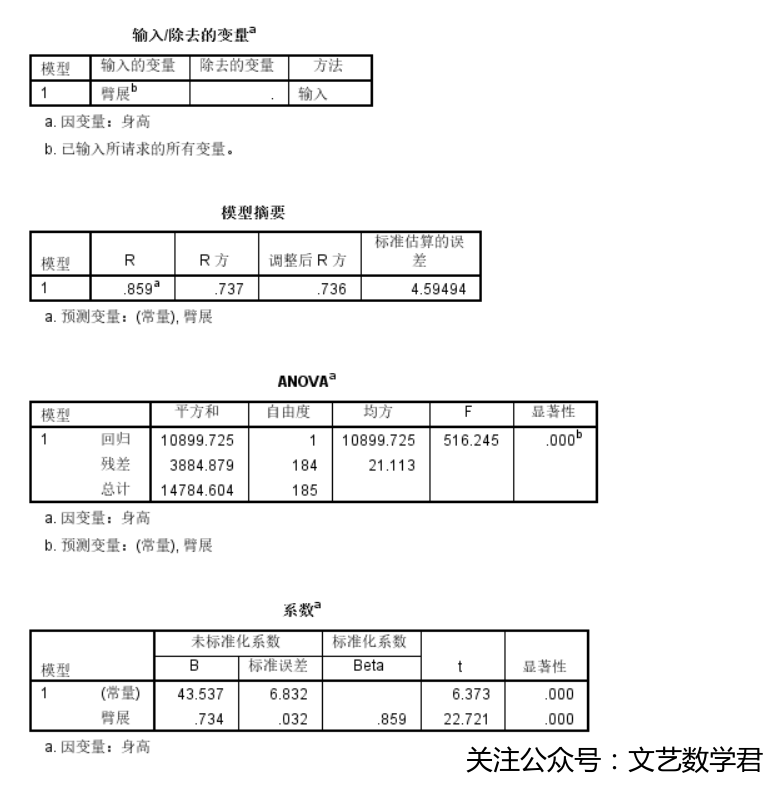
• 因此我们得到一个用臂展做自变量，身高做因变量的线性方程，对于身高缺失但臂展存在的球员数据可以利用该方程对其身高进行预测。

• 从本问中看出，身高与臂展间存在较强的线性关系，而且还可利用他们计算得到的方程进行数据预测，其他变量的关系与缺失数据的补充可用类似的方法得到。

二、探究变量间的共线性关系（以体重作为因变量为例）

从上例中我们可以看出，身高与臂展间存在很强的线性关系，如果在预测其他变量时同时在自变量中选择了身高和臂展，那么自变量中便存在了共线性关系，通常来说我们不希望自变量间存在共线性关系，这通常会导致回归系数值的不合理，因此我们需要寻找哪些变量与其他变量有共线性关系。常用的方法便是方差膨胀因子法。（关于膨胀因子的介绍可以看下面的链接：应用回归分析之寻找共线性变量）

• 利用SPSS具体操作步骤如下：

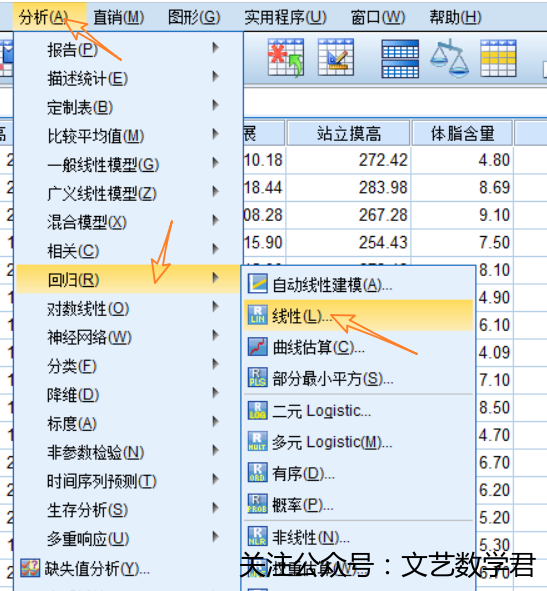
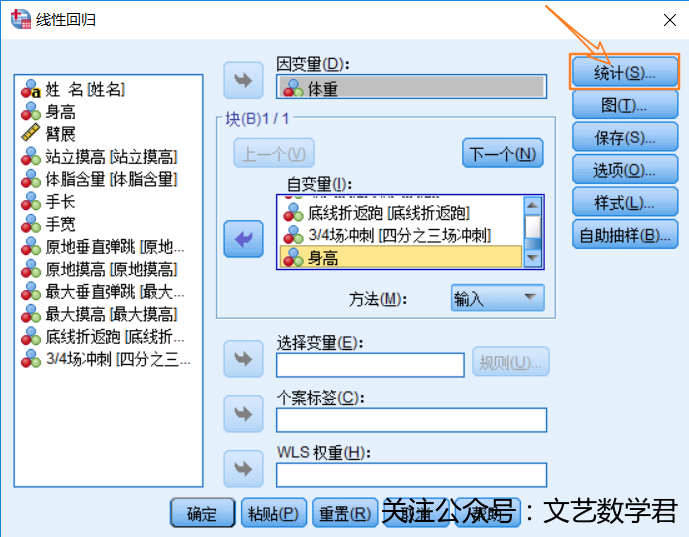
• 得到结果如下：

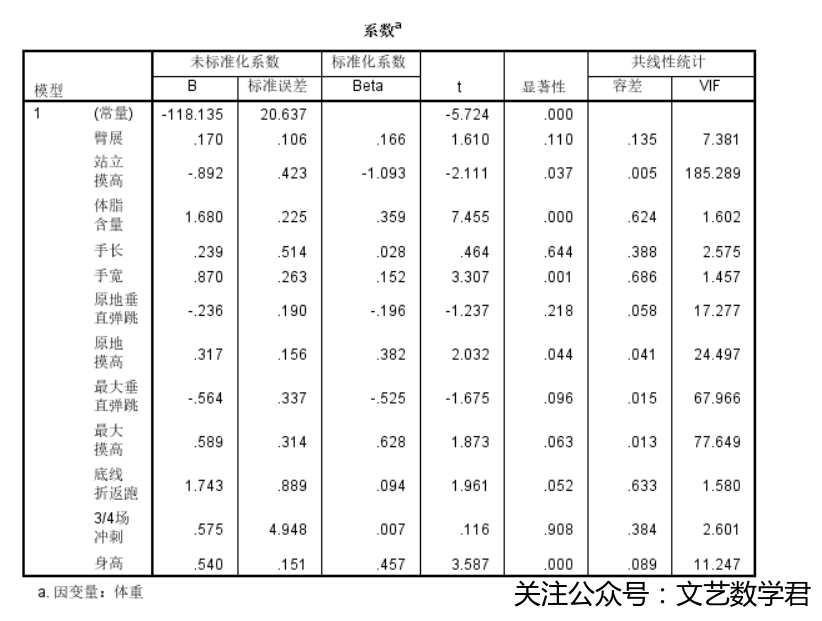
可以看到，在预测体重时，VIF>10的变量有站立摸高，原地垂直弹跳，原地摸高，最大垂直弹跳，最大摸高以及身高，说明这些变量各自与其他自变量间存在很强的共线性关系，在把这些变量选为自变量预测体重时要慎重。

三、寻找代表变量

从之前问题中可以看出，静态体测变量与动态体测变量各自所包含的变量存在较强的线性关系，因此我们希望从两个中各选一个或几个变量来概括某名球员的身体素质。这里我们使用的方法为主成分分析法。

关于主成分分析的方法我们会在多元回归的时候详细介绍，下面我们就简单介绍一下主成分分析法的数学原理：

主成分分析法

基本原理就是将一个矩阵中的样本数据投影到一个新的空间中去。对于一个矩阵来说，将其对角化即产生特征根及特征向量的过程，也是将其在标准正交基上投影的过程，而特征值对应的即为该特征向量方向上的投影长度，因此该方向上携带的原有数据的信息越多。

是希望用较少的变量去解释原来资料中的大部分变量，将我们手中许多相关性很高的变量转化成彼此相互独立或不相关的变量。通常是选出比原始变量个数少，能解释大部分资料中变量的几个新变量，即所谓主成分，并用以解释资料的综合性指标。由此可见，主成分分析实际上是一种降维方法。

1.将原始数据按行排列组成矩阵X

2.对X进行数据标准化，使其均值变为零

3.求X的协方差矩阵C

4.将特征向量按特征值由大到小排列，取前k个按行组成矩阵P

5.通过计算Y = PX，得到降维后数据Y

6.用下式计算每个特征根的贡献率Vi;Vi=xi/(x1+x2+........)

下面我们看一下具体使用SPSS操作主成分分析的步骤：

1、静态变量代表变量的选择

2、动态变量选择

结果如下

1、静态变量

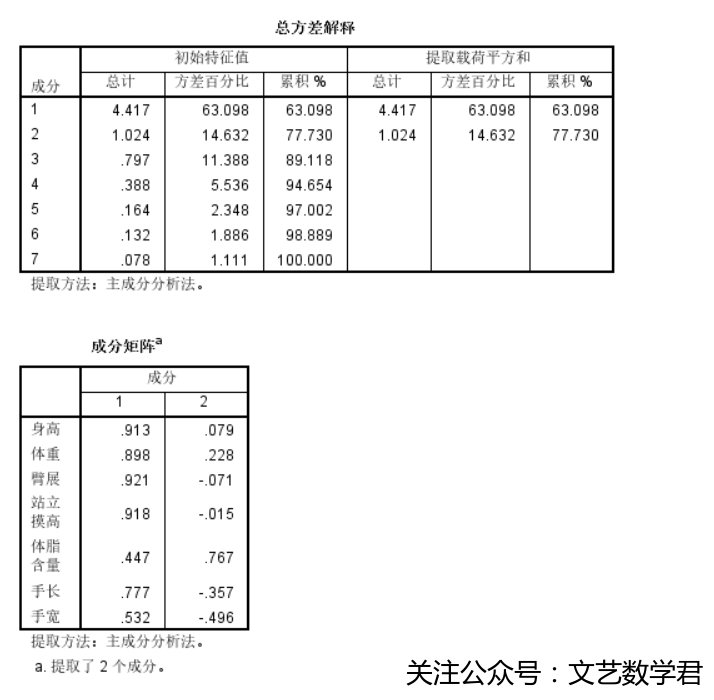
可以看到从所有静态变量中提取了2个主成分，而在属于这2个主成分的各自变量中，臂展与成分1相关系数绝对值最大，体脂含量与成分2相关系数绝对值最大，因此在一个球员所有静态数据中其臂展与体脂含量最能说明他的静态身体素质。

2、动态变量

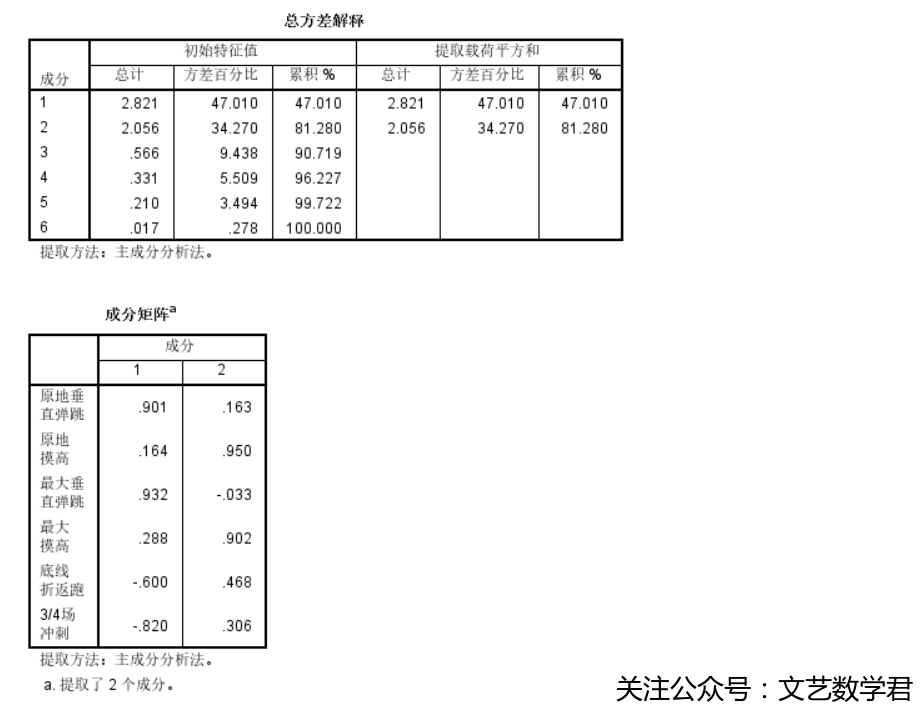
可以看到从所有动态变量中提取了2个主成分，而在属于这2个主成分的各自变量中，最大垂直弹跳与成分1相关系数绝对值最大，原地摸高与成分2相关系数绝对值最大，因此在一个球员所有动态数据中其最大垂直弹跳与原地摸高最能说明他的动态身体素质。

结语

到这里，我们就完成了应用回归分析相关的文章了，前面把每一个知识点进行拆开解释，同时使用mathematica和spss来进行说明，这个最后一篇，使用一个例子，来把之前学到的东西用到了一起。

谢谢大家的支持。