应用回归分析之寻找共线性变量(mathematica版本)

这是寻找共线性变量的第二篇文章，是使用mathematica来寻找共线性变量，我们还是从例题中来看如何使用mathematica来寻找共线性变量。

例题解析

变量解释：

• Y：房屋的售价（千美元）
• X1：税款（地方税、教育税、县税）(千美元)
• X2：盥洗室间数
• X3：大小（千平方英尺）
• X4：起居空间（千平方英尺）
• X5：车库间数
• X6：房间数
• X7：卧室数
• X8：房龄（年）
• X9：壁炉数

数据如下：

{X1,X2,X3,X4,X5,X6,X7,X8,X9,Y}：
{{4.92, 1., 3.47, 1., 1., 7., 4., 42., 0., 25.9}, {5.02, 1., 3.53, 1.5, 2., 7., 4., 62., 0., 29.5}, {4.54, 1., 2.28, 1.17, 1., 6., 3., 40., 0., 27.9}, {4.56, 1., 4.05, 1.23, 1., 6., 3., 54., 0., 25.9}, {5.06, 1., 4.45, 1.12, 1., 6., 3., 42., 0., 29.9}, {3.89, 1.,4.45, 0.99, 1., 6., 3., 56., 0., 29.9}, {5.9, 1., 5.85, 1.24, 1., 7., 3., 51., 1., 30.9}, {5.6, 1., 9.52, 1.5, 0., 6., 3., 32., 0., 28.9}, {5.83, 1., 6.43, 1.23, 2., 6., 3., 32., 0., 35.9}, {5.3, 1., 4.99, 1.55, 1., 6., 3., 30., 0., 31.5}, {6.27, 1., 5.52, 0.98, 1., 5., 2., 30., 0., 31.}, {5.96, 1., 6.67, 1.12, 2., 6., 3., 32., 0., 30.9}, {5.05, 1., 5., 1.02, 0., 5., 2., 46., 1., 30.}, {8.25, 1.5, 5.15, 1.66, 2., 8., 4., 50., 0., 36.9}, {6.7, 1.5, 6.9, 1.49, 1.5, 7., 3., 22., 1., 41.9}, {7.78, 1.5, 7.1, 1.38, 1., 6., 3., 17., 0., 40.5}, {9.04, 1., 7.8, 1.5, 1.5, 7., 3., 23., 0., 43.9}, {5.99, 1., 5.52, 1.26, 2., 6., 3., 40., 1., 37.9}, {7.54, 1.5, 5., 1.69, 1., 6., 3., 22., 0., 37.9}, {8.8, 1.5, 9.89, 1.82, 2., 8., 4., 50., 1., 44.5}, {6.08, 1.5, 6.73, 1.65, 1., 6., 3., 44., 0., 37.9}, {8.36, 1.5, 9.15, 1.78, 2., 8., 4., 48., 1., 38.9}, {8.14, 1., 8., 1.5, 2.,7., 3., 3., 0., 36.9}, {9.14, 1.5, 7.33, 1.83, 1.5, 8., 4., 31., 0., 45.8}}

==1.方差膨胀因子法寻找共线性变量==

• 操作：

在mathematica中可以使用命令lm["VarianceInflationFactors"]来查看方差膨胀因子

• 分析:
• 如图可以看到各个变量的VIF值，即方差膨胀因子。
• 关于方差膨胀因子的计算公式 记Rj2为预测变量Xj关于其他预测变量做回归的得到的复相关系数之平方，那么Xj的方差膨胀因子为： VIFj=1/（1-Rj2）, j=1,……,p , 其中p为预测变量的个数

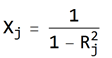
• 原理:

• 若预测变量间不存在任何线性关系，那么Rj2将为0，而VIFj就为1。 当Rj2趋于1，即表明预测变量间存在线性关系，则VIFj趋于无穷。

• 判断方法：

VIF超过10是多重共线性可能对估计带来麻烦的一个信号。

==2.通过相关系数特征根法寻找贡献性变量==

• 操作：

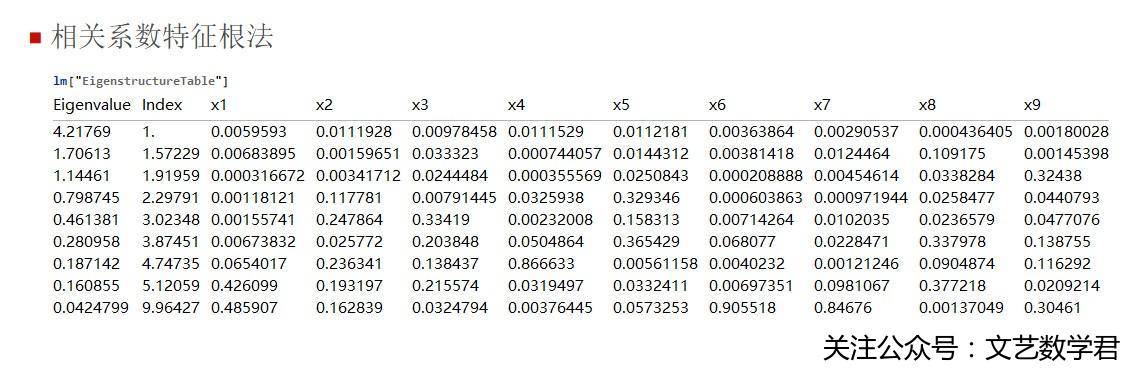
• 分析:

• 如图第一列中可以看到各个特征值，较小的（接近零）特征值就预示着共线性的存在

• 接近零特征值的个数就是共线性关系的个数

• 然后在接近零特征值对应的行中方差成分（Variance Proportions）中值较大的变量，它们便是存在共线性关系的变量