文章目录(Table of Contents)
前言
这一篇是讲关于应用回归分析里的自相关检验,我们通过一个例子来进行讲解。
例题解析
题目描述:
石油产量数据:表中数据是1880-1988年间以百万桶计的世界原油年产量,数据取自Moore和McCabe。采用ln(barrels)对年份做线性回归拟合。
- 计算Durbin-Watson统计量,从中你能得关于相关性存在的什么结论?
- 比较游程数与它们的期望值和标准差,从中你能得到关于相关性存在的什么结论?
数据如下
- {{year, barrels}:
- {1880., 30.}, {1890., 77.}, {1900., 149.}, {1905., 215.}, {1910., 328.}, {1915., 432.}, {1920., 689.}, {1925., 1069.}, {1930., 1412.}, {1935., 1655.}, {1940., 2150.}, {1945., 2595.}, {1950., 3803.}, {1955., 5626.}, {1960., 7674.}, {1962., 8882.}, {1964., 10310.}, {1966., 12016.}, {1968., 14104.}, {1970., 16690.}, {1972., 18584.}, {1974., 20389.}, {1976., 20188.}, {1978., 21922.}, {1980., 21722.}, {1982., 19411.}, {1984., 19837.}, {1986., 20246.}, {1988., 21338.}}
SPSS解答
第一问解答
首先计算D-W统计量:
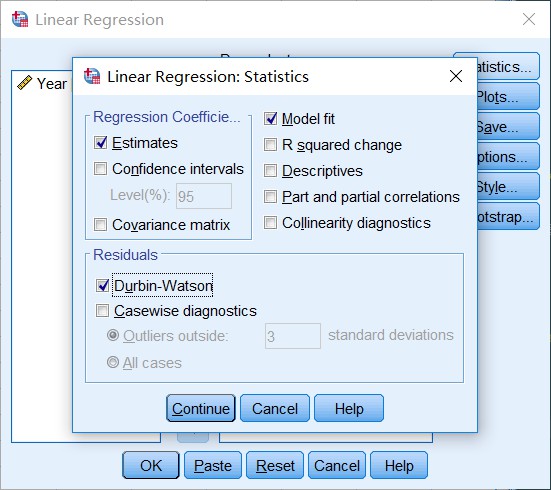
看一下分析的结果:
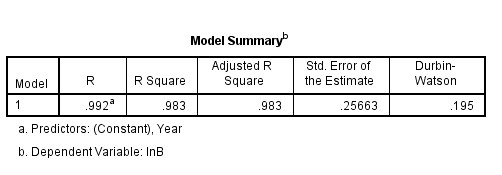
从中可以看出d=0.195。
接下来我们对上面的结果进行分析:
检验假设:
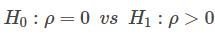
我们有:d = 0.195
当 n = 29, p = 1 时,查表可得:
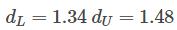
于是可以得到:
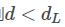
所以应该拒绝原假设,也就是自相关存在。
第二问解答
首先画残差图:
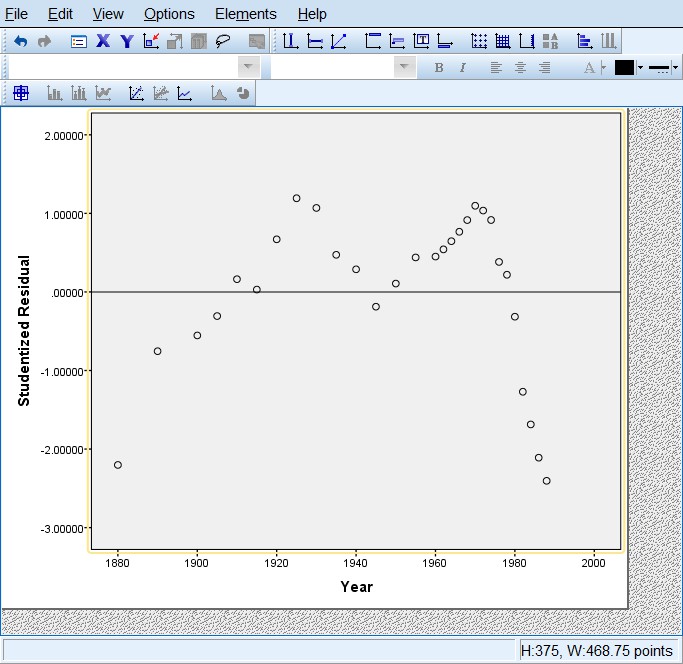
从图中我们可以数出,游程数runs=5。
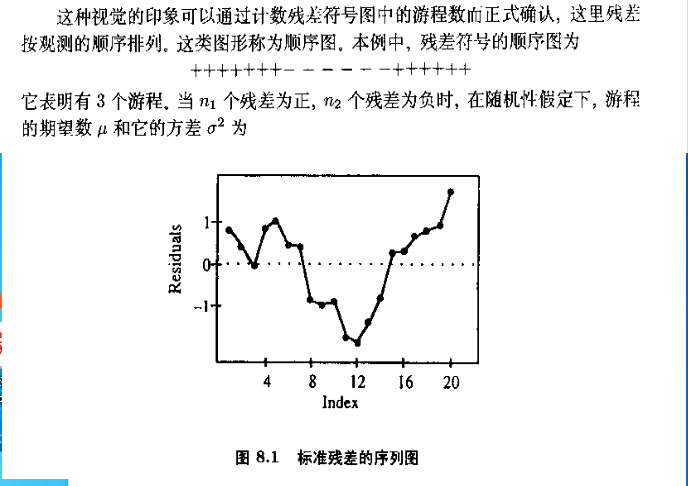
关于游程数的定义:残差穿过x-轴的次数+1,可以看一下下面这张图:
计算期望值与标准差并分析:
从图中可以数出:
- 正的个数为:n_1 = 19
- 负的个数为:n_2 = 10
所以我们可以计算得:
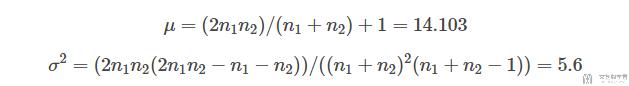
所以我们有:
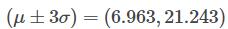
我们发现:
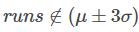
所以我们的结论是:自相关存在(与使用D-W统计量分析的结果相同)
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-












评论