应用回归分析之非线性模型变换为线性模型（spss版本）

例题解析

题目描述： 石油产量数据：表中数据是1880-1988年间以百万桶计的世界原油年产量，数据取自Moore和McCabe

(a)构造一个石油产量(OLL)对年份的散点图，并观察图像中点的散布呈非线性状，为了对这些数据拟合线性模型，必须对OLL做变换

(b)构造log(OLL)对年份的散点图。

(c)将log(OLL)对年份做线性回归，评价模型的拟合效果

(d)构造残差的标准序列图，该图显示了哪一条标准假定被违反了？

数据如下：

{{1880., 30.}, {1890., 77.}, {1900., 149.}, {1905., 215.}, {1910., 328.}, {1915., 432.}, {1920., 689.}, {1925., 1069.}, {1930., 1412.}, {1935., 1655.}, {1940., 2150.}, {1945., 2595.}, {1950., 3803.}, {1955., 5626.}, {1960., 7674.}, {1962., 8882.}, {1964., 10310.}, {1966., 12016.}, {1968., 14104.}, {1970., 16690.}, {1972., 18584.}, {1974., 20389.}, {1976., 20188.}, {1978., 21922.}, {1980., 21722.}, {1982., 19411.}, {1984., 19837.}, {1986., 20246.}, {1988., 21338.}}

SPSS

==1.a问解答==

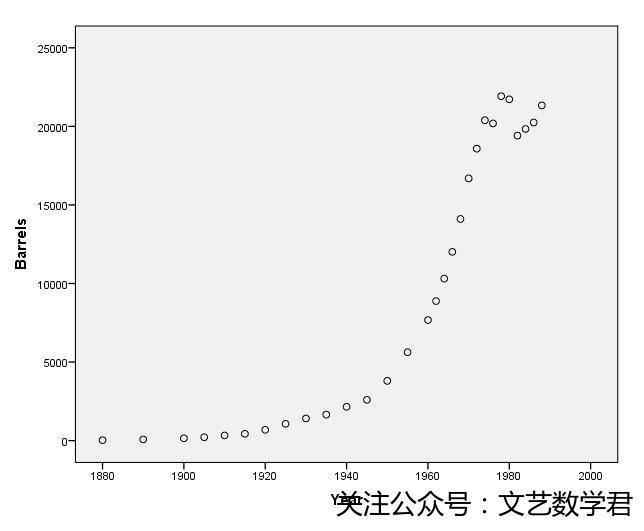
从图中可以看出，石油产量明显与年份不成线性关系，因此我们要进行变量变换将其转化为线性模型进行建模，初步观察其特点，我们猜想其具有指数模型，我们可以将两边取对数转化为线性模型

==2.b问解答==

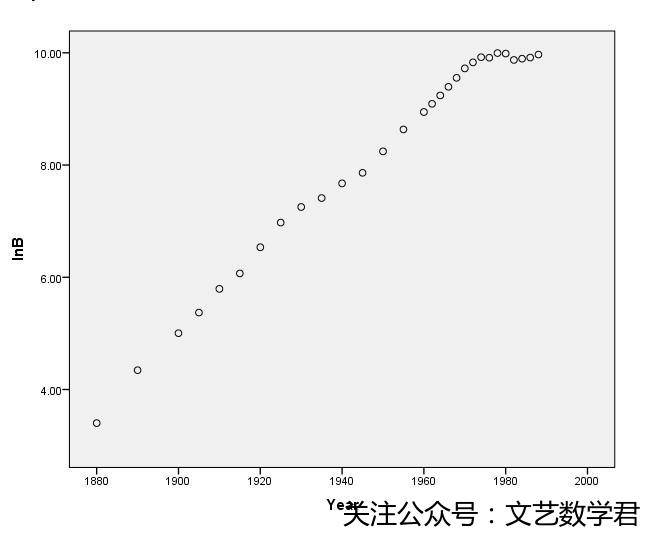
我们在取完对数后绘制的图形如上，可以观察到点基本分布在一条直线附近了，因此我们可以用线性模型进行拟合

==3.c问解答==

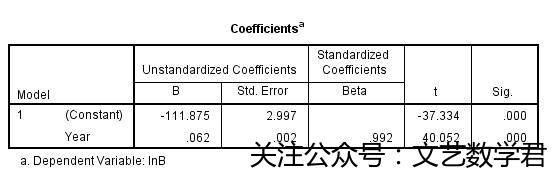
线性回归结果如图，可见方程为 lnB=-111.875+0.062Y+ε

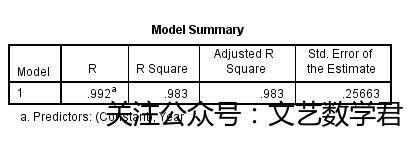
拟合优度如图，可见拟合程度较好

==4.d问解答==

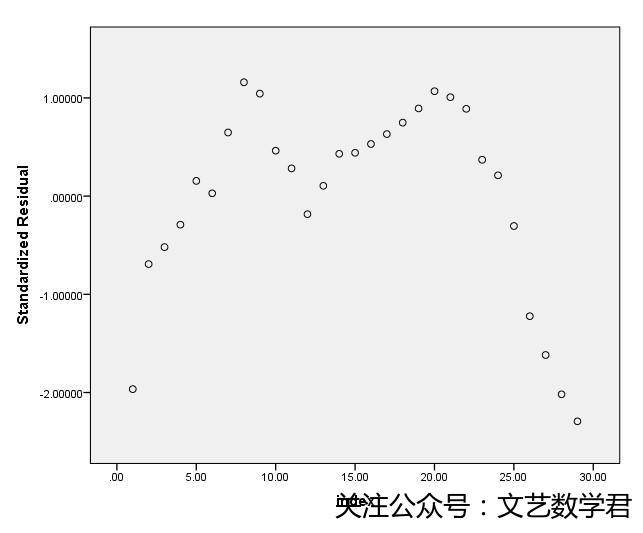
绘制残差序列图如上，我们发现残差并不是呈带状随机分布的，而是有明显的函数规律，这与之前误差之间相互独立的标准假定相违背