文章目录(Table of Contents)
例题解析
我们直接看一个例题,例题的数据如下:
- {X1,X2,X3,X4,X5,X6,Y}:
- {{830., 234289., 2356., 1590., 107608., 1947., 60323.}, {885., 259426., 2325., 1456., 108632., 1948., 61122.}, {882., 258054., 3682., 1616., 109773., 1949., 60171.}, {895., 284599., 3351., 1650.,110929., 1950., 61187.}, {962., 328975., 2099., 3099., 112075., 1951., 63221.}, {981., 346999., 1932., 3594., 113270., 1952., 63639.}, {990., 365385., 1870., 3547., 115094., 1953., 64989.}, {1000., 363112., 3578., 3350., 116219., 1954., 63761.}, {1012., 397469., 2904., 3048., 117388., 1955., 66019.}, {1046., 419180., 2822., 2857., 118734., 1956., 67857.}, {1084., 442769., 2936., 2798., 120445., 1957., 68169.}, {1108., 444546., 4681., 2637., 121950., 1958., 66513.}, {1126., 482704., 3813., 2552., 123366., 1959., 68655.}, {1142., 502601., 3931., 2514., 125368., 1960., 69564.}, {1157., 518173., 4806., 2572., 127852., 1961., 69331.}, {1169., 554894., 4007., 2827., 130081., 1962., 70551.}}
SPSS
我们首先是使用spss来进行操作
==1.岭迹图法==
原理解释:
回归分析中常用的最小二乘法是一种无偏估计。对于一个适定问题,X通常是列满秩的Xθ=y。
当X不是列满秩时,或者某些列之间的线性相关性比较大时,X^T X的行列式接近于0,即X^T X接近于奇异,上述问题变为一个不适定问题,此时,计算(X^T X)^(-1)时误差会很大,传统的最小二乘法缺乏稳定性与可靠性。
为了解决上述问题,我们需要将不适定问题转化为适定问题:我们为上述损失函数加上一个正则化项,变为:‖Xθ-y‖^2 + ‖Γθ‖^2,其中,我们定义Γ=kI,于是:θ(k)=[(X^T X+kI)]^(-1) X^T y,其中I是单位矩阵。
随着k的增大,θ(k)各元素θ_i (k)的绝对值均趋于不断变小,它们相对于正确值θ_i的偏差也越来越大。k趋于无穷大时,θ(k)趋于0。其中,θ(k)随k的改变而变化的轨迹,就称为岭迹。实际计算中可选非常多的k值,做出一个岭迹图,看看这个图在取哪个值的时候变稳定了,那就确定k值了。
操作:
上面讲完原理,下面我们讲一下使用spss来做岭回归。
首先我们导入数据:
接着输入代码,如下图所示:
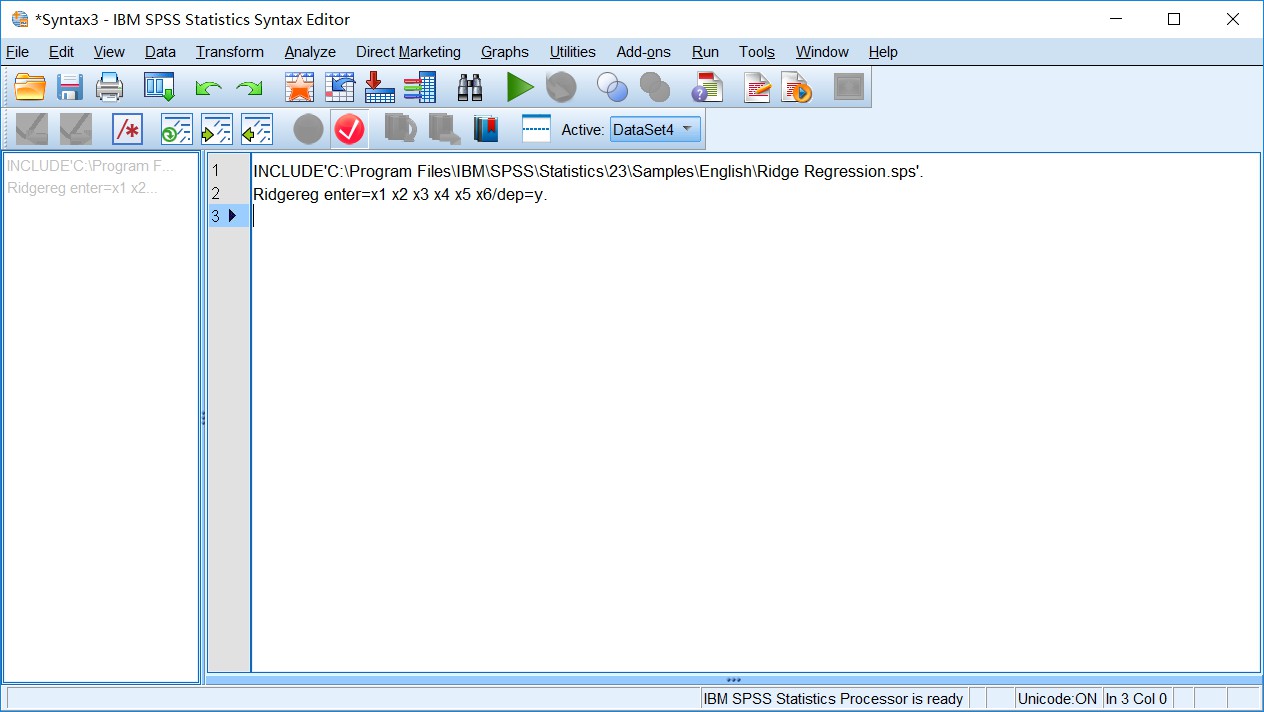
关于代码文件,如下所示:
使用spss做岭回归,需要用到spss自带的Ridge Regression.sps文件
- INCLUDE'C:\Program Files\IBM\SPSS\Statistics\23\Samples\English\Ridge Regression.sps'.
- Ridgereg enter=x1 x2 x3 x4 x5 x6/dep=y.
之后点击Run->All
之后就能看到运行的结果了
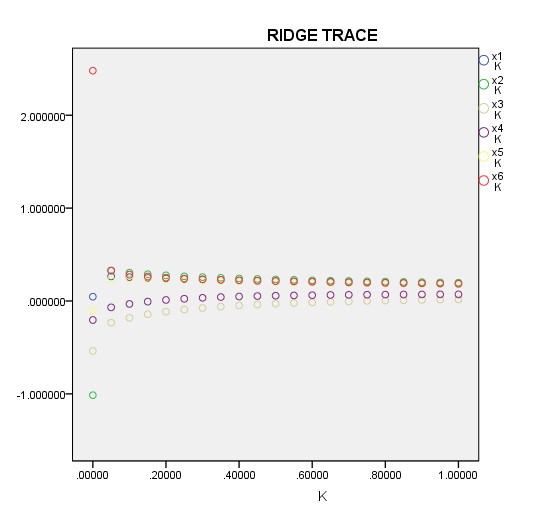
分析:
图中参数k可称为偏倚参数,随着k从0开始逐渐增大,估计的偏倚也随之增大。另一方面,总方差却是k的一个减函数。如果k无限制地增大下去,所有回归系数的估计都将趋向于0。岭回归的想法就是选一个k值,使得总方差的减少量不超过偏倚的增加量。
在岭迹图中确定k值:
k值较小时有系数很不稳定,当k慢慢增大时回归系数的估计值会慢慢稳定下来,所以我们希望选取一个最小的、能使系数估计稳定的k值。
比如图中,我们可以选取k=0.5。
下面我们来计算系数:
- 当k = 0.5时,我们将在此条件下求解系数。
- 得到结果如图:
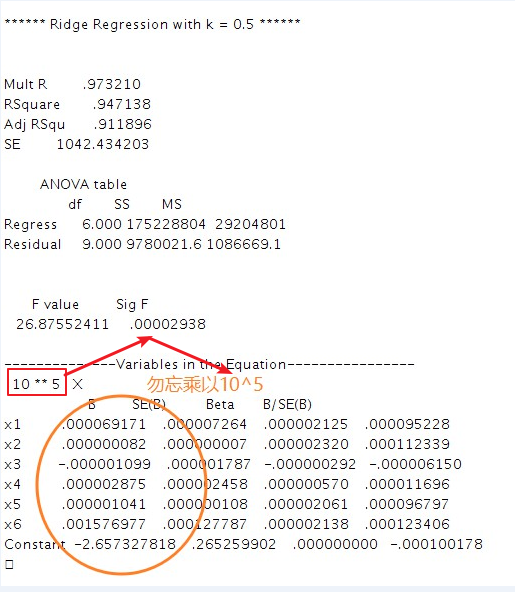
spss的代码如下所示:
- INCLUDE'C:\Program Files\IBM\SPSS\Statistics\23\Samples\English\Ridge Regression.sps'.
- Ridgereg enter=x1 x2 x3 x4 x5 x6/dep=y/k=0.5.
关于岭回归Mathematica的版本可以查看之前在csdn上写的博客,网址如下:
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-











评论