元胞自动机–一维双色

说明

从这一篇文章开始，我会用三篇文章，来讲完元胞自动机的一些概念。基本的顺序如下：

1. 一维双色元胞自动机
2. 一维多色元胞自动机（举k=3的例子）
3. 多维元胞自动机（举二维，k=2的例子）

下面开始第一篇文章，一维双色元胞自动机。

一维双色元胞自动机

简单概念

• 一个元胞自动机对每个元胞允许 k 个可能的值或者 "颜色" : 即一个格子上可以不止除了0和1；
• 并且具有至多有 r 个邻居的规则 : 周围r的格子对格子产生影响；

所以我们需要搞清楚的就是我们的元胞自动机是有几种状态，即k为多少，并且要知道半径r是多少。

对于一个元胞自动机，我们只需要每一种组合其对应的状态即可。

所以，为了表示方便，我们需要给每一种元胞自动机起一个名字，即其对应的变换规则是什么，下面我们就来看一下其命名的方式。

好吧，上面说得有点混乱，下面我们举例子来看。

例子--规则解释

还是通过我的手写来说明问题。

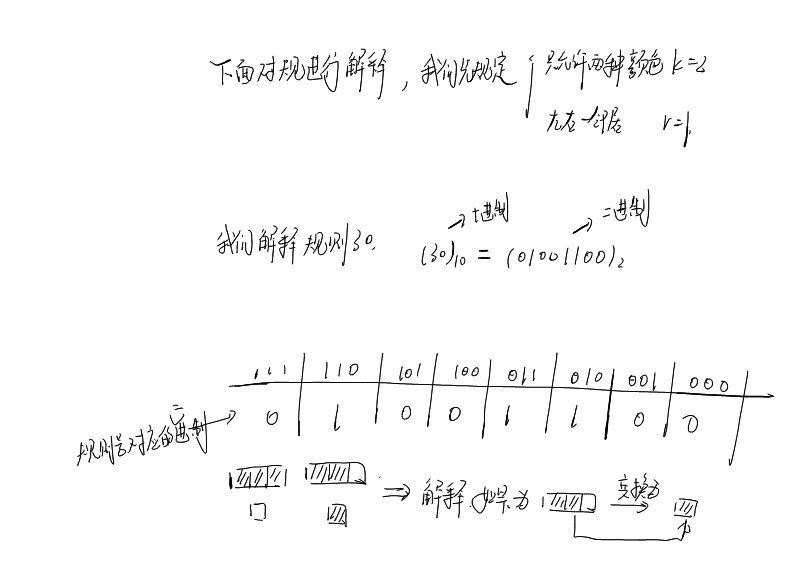
注意：上面图片中30的二进制写错了，应该是00011110，这样与下面能正确对应。感谢知乎的小伙伴指出问题。

通过上面的解释，应该就能看懂下面的规则图了。

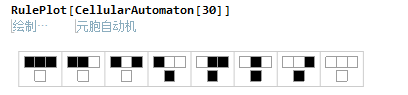
我们可以看一个具体变化的例子，初始为{1,0,0,0,0,1}，使用规则30，进行两次演变，得到下面的结果。

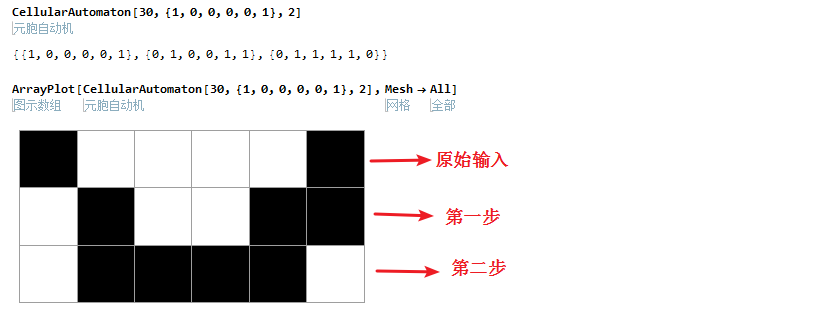
我用手写体来说明一下

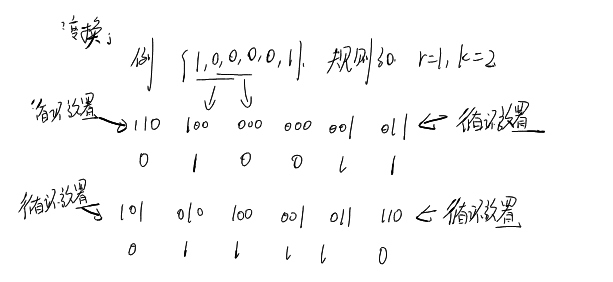
通过上面的解释，应该能理解了元胞自动机是如何做变换的了吧，下面我们看一下做100次演变之后的样子。

例子--关于mathematica实现元胞自动机

mathematica实现元胞自动机和上面过程是差不多的，先把你要的演变知道，计算其对应的规则号就可以了。

下面说几个mathematica实现元胞自动机的时候可能会用到的几个点。

给定一个初始，在恒定背景下进行迭代

下面的这个例子是使用规则90，初始为{1,1}（这个可以看图中第一行中间为黑色，就是{1,1}），背景为0（白色）进行填充

可以解释一下上面参数的意思，第一个90是表示规则90， 接下来的{{1, 1}, 0}表示初始是{1,1}，背景是0，最后2演变两次。（这里默认颜色是两种，邻居是1，第二篇会讲如何使颜色变为多种）

我们看一下演变100次后的图像，可以看到有点类似谢尔宾斯基三角形

当然，我们可以固定初始点的偏移量，看下面的例子

固定偏移量, 初始两个相距的距离

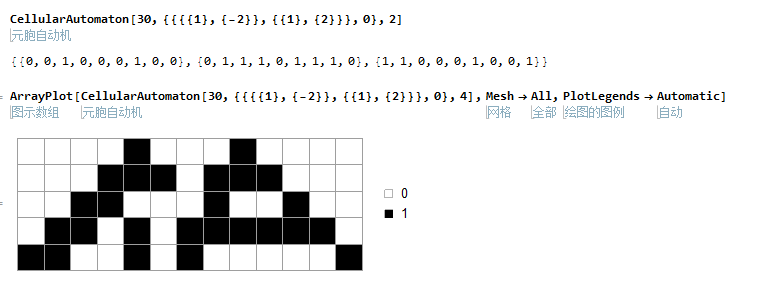
在这里可以看到是相距为2，我们可以看第一行，是10001，即是100，001，即离中心相距为2.

最后，我们看一下演变了100次后的形状

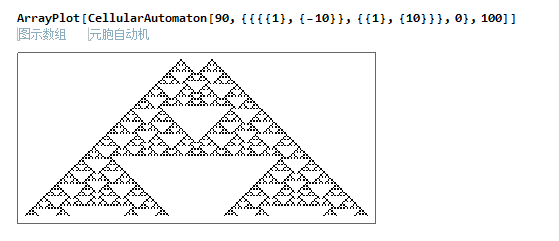
好了，第一篇关于元胞自动机的文章就到这里，这篇主要讲了关于元胞自动机里规则是如何设定的，和一维双色元胞自动机是如何演变的。

下一篇文章会介绍一维多色元胞自动机，下一篇再见。

一些建议

如果你对mathematica不熟悉的话，建议首先看一下mathematica入门教程：Mathematica快速入门，大概话两三天可以看完这个教程，看完之后可以对mathematica有一个大概的了解。

如果觉得基础掌握的差不多了，可以看一下下面的习题的链接，Mathematica入门习题，找10--20个做一下，大概两个小时左右，之后在看这个教程会好一些。

一些其他资料的链接：

点击下面的链接可以查看本网站所有更新完毕的系列 ： 文艺数学君各系列文章汇总

关于元胞自动机的更多内容可以查看下面的链接：元胞自动机文章汇总|文艺数学君