元胞自动机–一维多色

经过了前面的元胞自动机的讲解，相信大家对于一维单色的已经有所了解了，下面我们就来讲一下一维多色的情况，我会以三色为例子，来进行讲解。

一维三色元胞自动机

其实对于一种元胞自动机，我们演化的规则是很好写的，我们要做的就是把这些规则和规定的记号联系起来，之前k=2的时候是使用二进制，现在有三种颜色，二进制已经不能够表示了三种颜色了，所以在这里使用三进制。

下面我来解释一下规则921408

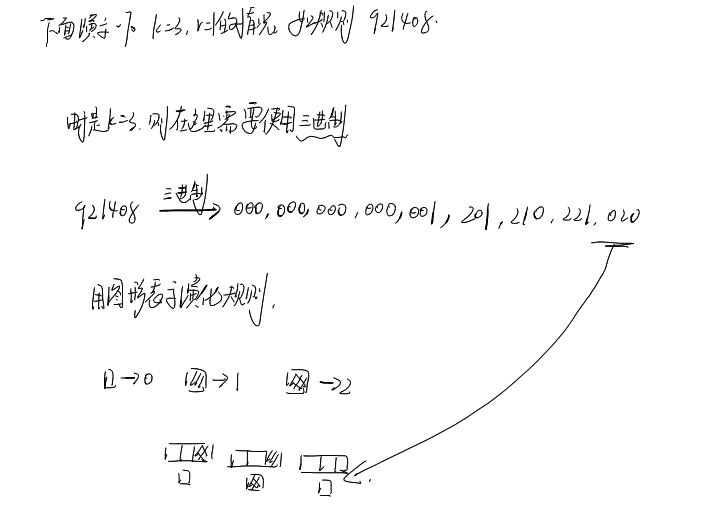
这样，我们就可以把每一种演化和其规则号对应起来了

我们看一下规则921408的演化图像，和我们之前推导的是不是一样的，可以从下面的图中看出，是和我们写的是一样的。（我们只推导了右下角的三个）

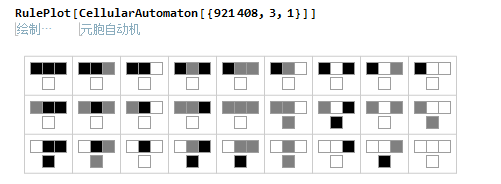
我们看一下演化5步之后的图像

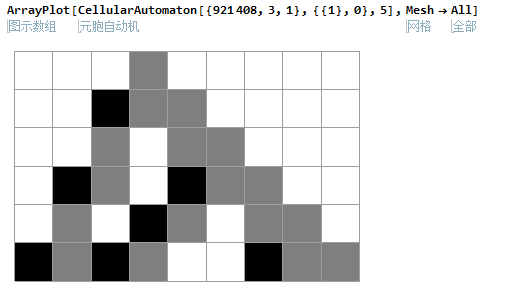
我们可以看一下演化100步之后的效果图

直接规定变换的元胞自动机

下面我们来讲一个加法的元胞自动机，将相邻结果相加后mod3

下面我用手写体来说明一下演化过程是如何进行的。

图中是进行三步之后的图，我们多演化几次看一下

这是演化了100次之后的效果，还是挺好看的。