多维元胞自动机

这一篇会讲多维的元胞自动机，我会以二维作为例子来讲。这一篇应该会是元胞自动机基础的最后一篇了，关于后面是否会有应用篇，恩，再说，可能不会有，看我心情。

二维的规则定义

由于从一维到二维，会增加很多演变的种类，什么意思呢

就是从8增长到了512，这还是双色的，邻居为1的情况，就是说一个二维的元胞自动机的演变我要定义512种，恩，太多了，所以我们一般不会这么用。（如果你上面没看懂没关系，看下面就可以，下面是常用的）

那么我们是如何定义二维的规则呢，没错，就是用邻居的总和来定义，常见的有三种邻居总和的定义，下面我们一一来说明，每个都通过一个例子来说明。

二维九邻居总和规则

这个顾名思义就是通过九个邻居的和来定义演变规则，因为每个格子只能是0或者1，所有一共有10种，为从0--9。

我们首先生成10个3*3的矩阵，用来一会看每个均值对应的变换（这里的生成方式比较巧妙，可以学习使用一下）

接着，我们计算每个均值对应的变换后的值，我们可以看到把对应的值看成二进制，转换为十进制就是规则号，14，这个要是不懂，可以看第一篇文章，我推导的地方。

最后就只需要把图画出来就可以了，这个方格不需要看具体0，1所在的位置，只需要看九个格子的总和即可。

我们可以看到上面我们手动画得规则和下面的规则图是一样的。

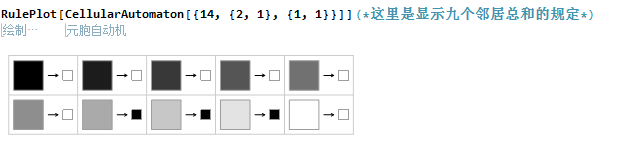
到这里，我们就明白了二维元胞自动机里的九近邻和的规则是如何定义的了。

接着，我们看一下演化的过程，其实也没什么好讲的，就和第一次讲的类似，大家自己推导一下就可以了。

我们最后看一下30步骤演化后的效果是什么样子的。

我们看一下在二维里面，如何设置初始的状态：

上面这样是直接定义了初始的点的位置。这样就可以修改初始状态了。

二维五邻居总和规则

其实这个五近邻和九近邻是很类似的，一个是九个格子的和，一个是五个格子的和，那我就大概说一下，如果你认真看了上面的，我相信你能举一反三，这里的不看也能想出来。恩...但是我还是会写的。

我们还是看一下他的规则，由于是五近邻，所有只有六种变换了，下面的图也是只要看五个格子的和就可以，不需要在意具体的位置。

我们看一下直接画他的规则图，来看看是否是一样的。

可以看到是一样的，我们可以计算出(110010)2==(50)10，即二进制110010等于十进制的50，即是这里的规则号。

二维五邻居外层总和规则

好了，讲一下最后一个，这个其实就是为了区分中心那个点和她周围的点，比如生命游戏里的规定，但是这样演化的数量就要变多，为了能把号码和变换能对应起来，所以把外面的数字加权了，具体说呢，就是中间的点1还是1，外面的如果是1，则要有两倍权重，为2。这样就有0--9十种情况了，这样就能对应起来了。

可以看一下下面的变换的规则为90的变换

再看一下下面和上面的对照，可以看到两者是一样的。

好了，到这里就把多维的也讲完了，怎么感觉想讲一下康威生命游戏呢，那看我时间吧，有空就再做一下康威生命游戏，这次的元胞自动机基础系列就到这里了，欢迎大家多多留言。