文章目录(Table of Contents)
问题来源
最近在一本书上看到要求x^2 + y^2 == 2 x与x^2 + y^2 + z^2 == 4相交得到的立体的体积,即圆柱与球相交得到的立体的体积。看答案需要座标变换之类的,但是想到之后这类问题我可能都会使用 Mathematica 来解决,于是决定用 Mathematica 来求一下,并画出圆柱与球相交得到的立体的形状。
问题解决
我们首先来看一下两个立体相交得到的是什么样子的图像,我们使用ContourPlot3D来画出相交的样子。
- ContourPlot3D[{x^2 + y^2 == 2 x, x^2 + y^2 + z^2 == 4}, {x, -2,2}, {y, -2, 2}, {z, -2, 3},
- ContourStyle -> {{Opacity[.5]}, {Opacity[0.7]}},
- BoundaryStyle -> Directive[Red, Thick],
- Mesh->None
- ]

可以看到上面的图,但是感觉还是不够形象,我想要把这个相交的立体抠出来。不慌,我们有办法的。
- r = RegionPlot3D[ x^2 + y^2 <= 2 x && x^2 + y^2 + z^2 <= 4, {x, -2, 2}, {y, -2, 2}, {z, -2, 3}, Mesh->None]

可以看到这个就是抠出来的图形的样子。下面我们来求一下这个立体的体积。
- Integrate[Boole[x^2 + y^2 <= 2 x && x^2 + y^2 + z^2 <= 4], {x, -2, 2}, {y, -2,2}, {z, -2, 3}];
- >>16/9 (-4 + 3 Pi)
通过上面的办法就将体积计算出来了,和答案对了一下,是一样的。恩,以后就可以这么计算立体的体积了。
问题拓展--圆柱与圆柱相交
我们再来看一下圆柱与圆柱相交得到的立体的形状。
- ContourPlot3D[{x^2 + y^2 == 4, x^2 + z^2 == 4}, {x, -3, 3}, {y, -3,3}, {z, -3, 3},
- ContourStyle -> {{Opacity[.7]}, {Opacity[0.7]}},
- BoundaryStyle -> Directive[Red, Thick],
- BoxRatios -> {1, 1, 1},
- Mesh -> None
- ]
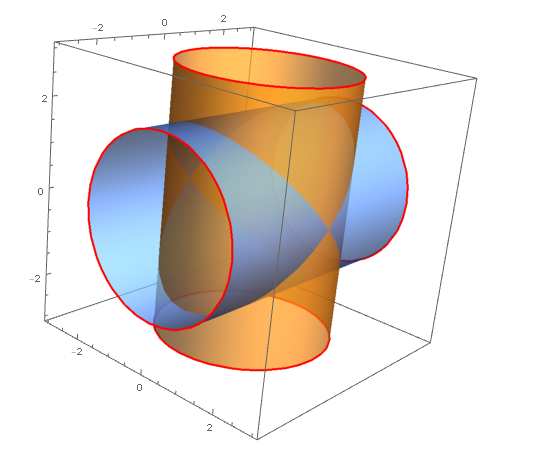
这样看还是看不清,我们把这个相交得到的立体抠出来看看。
- RegionPlot3D[
- x^2 + y^2 <= 4 && x^2 + z^2 <= 4, {x, -3, 3}, {y, -3, 3}, {z, -3, 3},
- PerformanceGoal -> "Quality",
- PlotPoints -> 50,
- Mesh -> None]

到这里我们就把我觉得比较常见的两种立体相交得到立体的样子画出来了。
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-













评论