基于矩阵分解的协同过滤

王 茂南
王 茂南
王 茂南
2827
文章
75
评论
2019年12月13日07:36:5721 5284字阅读17分36秒
摘要这一篇文章主要介绍基于矩阵分解的协同过滤算法, 会介绍常用的算法, 例如FunkSVD, 加入正则化, 加入偏置(BiasSVD). 同时会给出相关的代码实现.

简介

这一篇我们介绍关于基于矩阵分解的协同过滤的方法. 基于矩阵的协同过滤有以下的好处:

  • Matrix factorization techniques are usually more effective because they allow us to discover the latent features underlying the interactions between users and items.
  • Matrix factorization is simply a mathematical tool for playing around with matrices, and is therefore applicable in many scenarios where one would like to find out something hidden under the data.

参考资料

 

矩阵分解的协同过滤简单介绍

在推荐系统中, 我们有一些用户和一些商品. 这些用户会给这些商品进行打分 (或是用户会对某一个商品进行购买), 我们希望可以预测那些用户没有打分的物品, 用户对这些物品的喜爱程度.

假设现在有5个用户和4个商品, 用户对一些商品进行了打分, 打分分别是1-5. 我们可以将其信息使用矩阵进行保存, 如下图所示, 其中矩阵中的连字符表示该用户没有对这个商品进行评分.

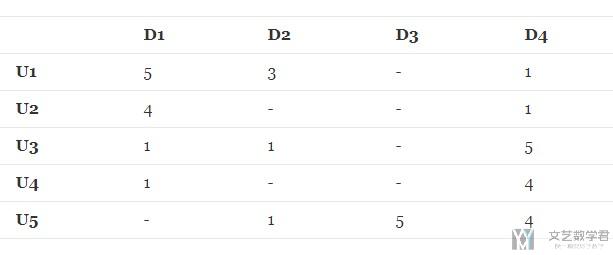
基于矩阵分解的协同过滤

我们的任务就是要预测上面表格中的缺失的数值, 使得这些数值也能给出和矩阵中现有的评级一致的内容.

 

一些解释

使用矩阵分解的方式来解决这类问题, 我们可以理解为因为有一些隐藏的因素会影响他们的购买决定.

例如, 有两个用户给同一个电影高分, 这可能是因为他们都喜欢动作类型的电影, 而电影是动作类型的. 因此, 如果我们可以发现这些隐藏变量, 我们就可以预测用户对于某个特定的物品的喜爱程度了.

同时, 我们需要假设, 每一个人或物的隐藏变量的个数是小于用户的个数和物品的个数的(因为实际情况下人和物是有很多的). 同时如果这些人与物之间没有共同点, 那么所谓的推荐系统也是没有价值的.

 

传统的奇异值分解SVD

说到矩阵分解, 我们首先想到了奇异值分解(SVD). 但是传统的SVD无法处理有缺失数据的情况. 如果没有缺失数据, 那么就不需要进行对评分的估计, 从而来进行推荐了. 于是, 我们有了下面的改进算法.

关于SVD的介绍(看一下目录): 矩阵运算与优化算法例题

 

FunkSVD算法

FunkSVD是对于传统SVD的改进, 使其可以用来解决在推荐系统中的问题. 我们下面进行详细的描述.

  • 假设我们有U个用户, D个商品.
  • 于是我们有了一个U*D大小的矩阵R, 这个矩阵包含所有用户对商品的评价.
  • 我们假设我们有K个隐变量 (latent features)
  • 我们的任务是, 我们希望可以找到两个矩阵, 矩阵P(U*K大小), 矩阵Q(D*K大小的), 是他们的乘积与原始矩阵R接近. 计算式子如下图所示:
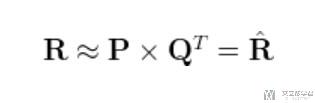
基于矩阵分解的协同过滤

其中:

  • 矩阵P的每一行代表某个人对于不同特征的热爱程度.
  • 矩阵Q的每一行代表某个事物拥有这个特征的程度.

我们使用下面的图进行解释, 例如矩阵P的第一行中第一个元素表示人A对科幻片的喜爱程度(这是一个人的性质), 矩阵Q的第一行第一个元素表示这个物品的科幻片的属性, 是否是科幻片.

我们就是将一个人的隐藏属性与一个物的隐藏熟悉进行相乘求和, 求出人对于这个物品的喜爱程度.

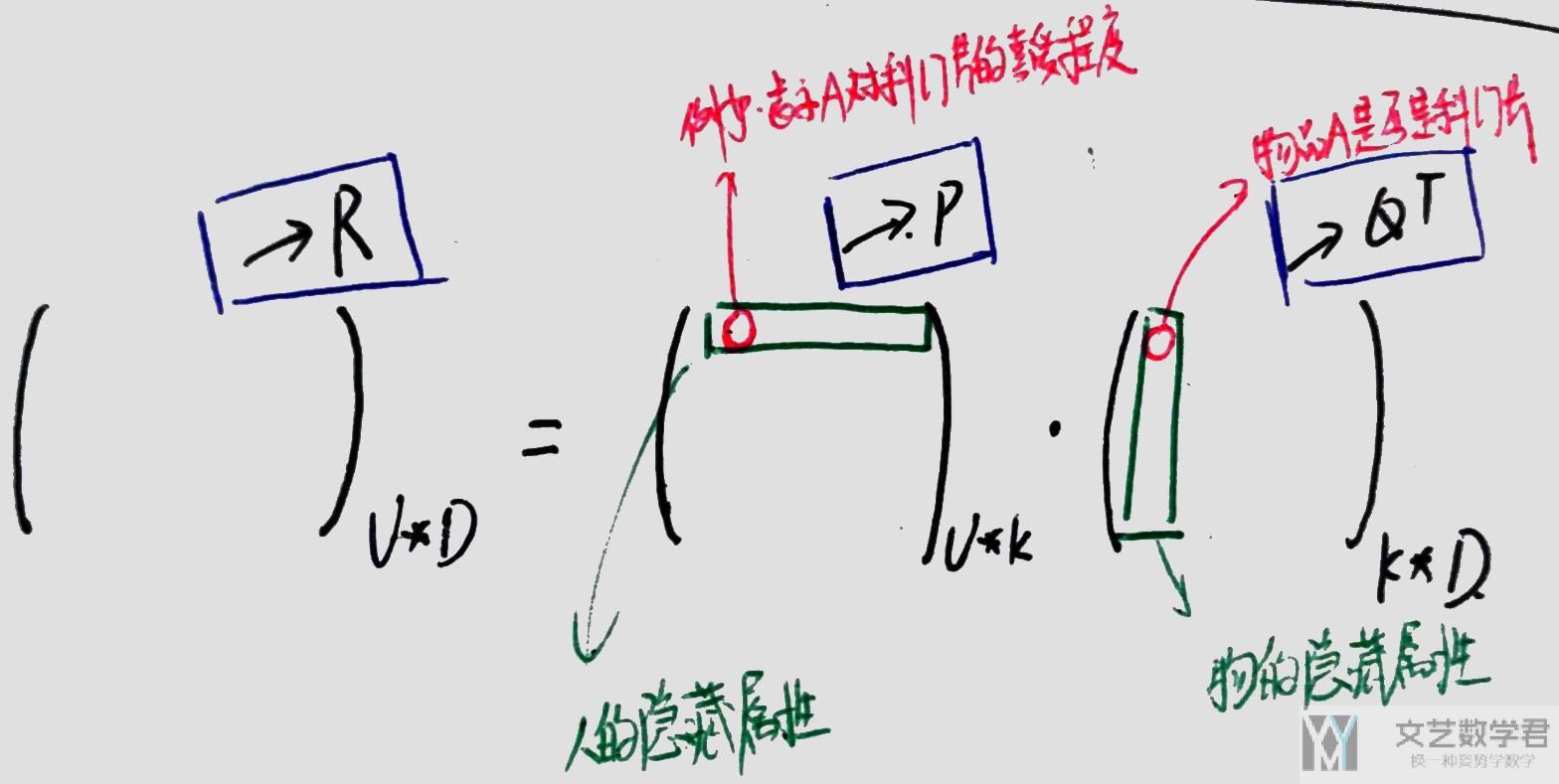
基于矩阵分解的协同过滤

我们将上面的写成向量相乘的方式, 一个人对一个物品的喜爱程度 (例如第i个人对第j件物品的喜爱程度), 可以通过下面的方式进行计算 (矩阵P的第i行, 矩阵Q的第j行, 两者进行相乘):

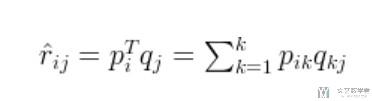
基于矩阵分解的协同过滤

接下来的问题就是, 我们需要找到一种方法, 可以求出上面的矩阵P和矩阵Q. 我们想到了一种直观的方式, 就是希望使得矩阵P和Q相乘得到的矩阵与原始矩阵R尽可能的接近, 也就是loss尽可能小.

我们可以使用下面的方式来定义他的loss, 我们计算他的预测值与真实值之间的差值(这里我们只考虑观测矩阵R中有的值, 那些unknown的值是不需要进行考虑的):

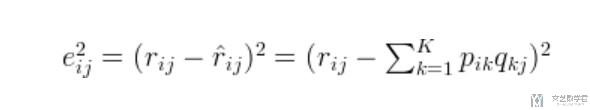
基于矩阵分解的协同过滤

为了使上面的loss可以最小, 我们使用梯度下降的方法来进行操作. 具体的梯度值可以查看上面的参考资料的第二个链接. (在计算的时候, 可以直接使用Pytorch的自动求导的功能)

下面是一张彩色的图片, 意思和上面要表达的差不多, 可以查看原图.

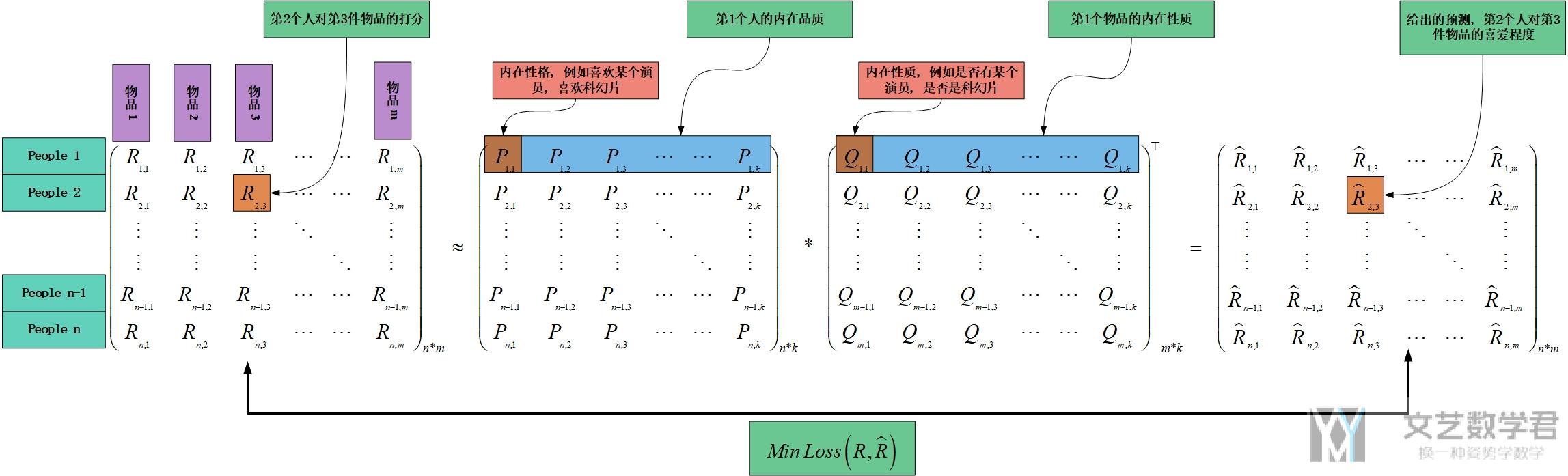
基于矩阵分解的协同过滤

FunkSVD+Regularization

上面介绍的是比较基础的矩阵分解的算法. 在这个算法的基础上, 会有很多的改进, 一种比较简单的改进就是加入正则化. 加入正则化的目的是希望系数不要太过于复杂, 在矩阵P和Q中不希望有太多太大的数.

下面是加入正则化之后的loss函数:

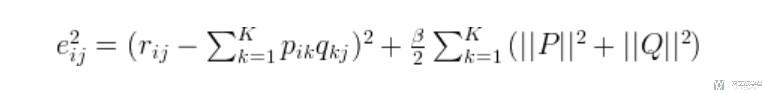
基于矩阵分解的协同过滤

在实际使用中, 上面的B一般取值在0.02左右. 同样也是使用梯度下降的方法来进行求解.

 

代码实现

我们在这里使用Pytorch来实现最优解的求值. 完整的代码如下所示:

  1. import numpy as np
  2. import pandas as pd
  4. import os
  5. import matplotlib.pyplot as plt
  6. from datetime import date,datetime
  7. import logging
  9. import torch
  10. from torch import nn
  11. from torch import optim
  12. from torch.autograd import Variable
  14. device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
  15. device
  17. # --------------------
  18. # 下面三种计算loss的方式
  19. # --------------------
  21. def PredictR(P, Q, R):
  22.     """
  23.     最基本的FunkSVD
  24.     """
  25.     R_pred = torch.mm(P, Q.t()) # 矩阵相乘
  26.     N,M = R.shape
  27.     loss = 0
  28.     for i in range(N):
  29.         for j in range(M):
  30.             if R[i][j] > 0:
  31.                 loss = loss + (R_pred[i][j]-R[i][j])**2
  32.     return loss
  34. def PredictRegularizationR(P, Q, R):
  35.     """
  36.     FunkSVD+Regularization
  37.     """
  38.     B = 0.02 # 正则话的系数
  39.     R_pred = torch.mm(P, Q.t()) # 矩阵相乘
  40.     N,M = R.shape
  41.     loss = 0
  42.     for i in range(N):
  43.         for j in range(M):
  44.             if R[i][j] > 0:
  45.                 loss = loss + (R_pred[i][j]-R[i][j])**2
  47.     loss = loss + B*((P**2).sum() + (Q**2).sum()) # 加上正则项
  48.     return loss
  50. def PredictRegularizationConstrainR(P, Q, R):
  51.     """
  52.     FunkSVD+Regularization+矩阵R的约束(取值只能是0-5, P,Q>0)
  53.     """
  55.     B = 0.1 # 正则话的系数
  56.     R_pred = torch.mm(P, Q.t()) # 矩阵相乘
  57.     N,M = R.shape
  58.     loss = 0
  59.     for i in range(N):
  60.         for j in range(M):
  61.             if R[i][j] > 0:
  62.                 loss = loss + (R_pred[i][j]-R[i][j])**2
  63.             elif R[i][j] == 0: # 下面是限定R的范围
  64.                 if R_pred[i][j] > 5:
  65.                     loss = loss + (R_pred[i][j]-5)**2
  66.                 elif R_pred[i][j] < 0:
  67.                     loss = loss + (R_pred[i][j]-0)**2
  69.     loss = loss + B*((P**2).sum() + (Q**2).sum()) # 加上正则项
  71.     # 限定P和Q的范围
  72.     loss = loss + ((P[P<0]**2).sum() + (Q[Q<0]**2).sum())
  73.     return loss
  75. if __name__ == "__main__":
  76.     # 原始矩阵R
  77.     R = np.array([[5.0, 3.0, 0.0, 1.0],
  78.     [4.0, 0.0 ,0.0 ,1.0],
  79.     [1.0, 1.0, 0.0, 5.0],
  80.     [1.0, 0.0, 0.0, 4.0],
  81.     [0.0, 1.0, 5.0, 4.0]])
  83.     N,M = R.shape
  84.     K = 2
  86.     R = torch.from_numpy(R).float()
  88.     # 初始化矩阵P和Q
  89.     P = Variable(torch.randn(N, K), requires_grad=True)
  90.     Q = Variable(torch.randn(M, K), requires_grad=True)
  92.     # -----------
  93.     # 定义优化器
  94.     # -----------
  95.     learning_rate = 0.02
  96.     optimizer = torch.optim.Adam([P,Q], lr=learning_rate)
  97.     lr_scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=1000, gamma=0.9) # 学习率每20轮变为原来的90%
  98.     # ---------
  99.     # 开始训练
  100.     # ---------
  101.     num_epochs = 5000
  102.     for epoch in range(num_epochs):
  103.         lr_scheduler.step()
  104.         # 计算Loss
  105.         loss = PredictRegularizationConstrainR(P, Q, R)
  106.         # 反向传播, 优化矩阵P和Q
  107.         optimizer.zero_grad() # 优化器梯度都要清0
  108.         loss.backward() # 反向传播
  109.         optimizer.step() # 进行优化
  110.         if epoch % 20 ==0:
  111.             print(epoch,loss)
  112.     # 求出最终的矩阵P和Q, 与P*Q
  113.     R_pred = torch.mm(P, Q.t())
  114.     print(R_pred)
  115.     print('-'*10)
  116.     print(P)
  117.     print('-'*10)
  118.     print(Q)

上面有三个函数, 分别对应三种计算loss的方式.

  • PredictR: 基本的FunkSVD的思想
  • PredictRegularizationR: 基本的FunkSVD+正则化
  • PredictRegularizationConstrainR: FunkSVD+正则化+限制R, P, Q的范围, 其中我们希望R的范围在0-5之间, P和Q都可以大于0.

我们使用上面的第三种方式来计算loss, 最后得到我们预测的R如下所示, 可以看到预测的结果还是很不错的.

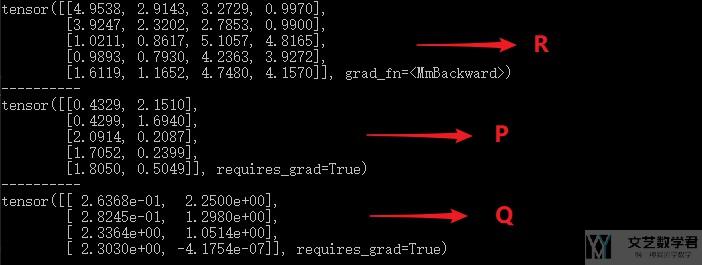
基于矩阵分解的协同过滤

代码链接: FunkSVD相关代码

 

BiasSVD算法

这个算法是在上面的算法的基础上加上bias(偏置), 他的想法就是认为人和物有一些固定的因素. 有一些内在的东西. 他包含下面的两种偏置:

  • 用户偏置 : 可以看作用户的性格 , 个人的品质等因素
  • 物品偏置 : 例如物品的价格 , 物品的质量等

我们看一个下面的例子, 原本使用FunkSVD就是两个矩阵的乘积, 这里需要加上两个常数.

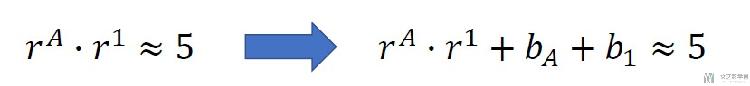
基于矩阵分解的协同过滤

大概就是上面的式子的意思, 我们在这里加上了两个偏置, 分别和人和物有关. 于是loss函数就变成了下面的样子.

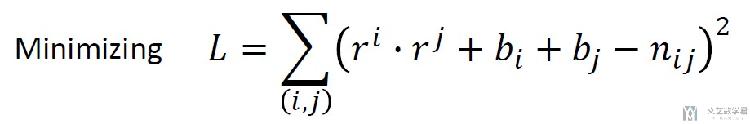
基于矩阵分解的协同过滤

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2019年12月13日07:36:57
  • 转载请务必保留本文链接：https://mathpretty.com/11495.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen:

评论：2   其中：访客  1   博主  1
    • CT0011111123S
      CT0011111123S
      2020年8月13日 下午10:03 1F
      回复

      PyTorch有一些问题而且性能比较慢，建议看https://blog.fastforwardlabs.com/2018/04/10/pytorch-for-recommenders-101.html

        • 王 茂南
          王 茂南
          2020年8月14日 上午8:22 B1
          回复

          @ CT0011111123S 我大致看了一下, 他文章最后好像没说Pytorch的一些问题, 他原文是, “We thought PyTorch was fun to use; models can be built and swapped out relatively easily. When we did encounter errors, most of them were triggered by incorrect data types.” (不过这一篇写的非常不错)