模型评价指标说明与实践–混淆矩阵的说明

简介

这一部分介绍一下模型的一些评价指标，这些指标是经常用到的，用来评价模型的好坏。

还是将参考资料放在最上面。

参考资料

• 主要参考来自这个链接 : Understanding Confusion Matrix
• 部分参考内容 : CSDN-理解准确率(accuracy)、精度(precision)、查全率(recall)、F1

指标说明

上面是一些指标的计算的公式，可以结合最后的一个例子进行理解.

TP, TN, FP, FN的简单说明

对于一个二分类来说，我们对于预测值和实际值有下面四种组合方式

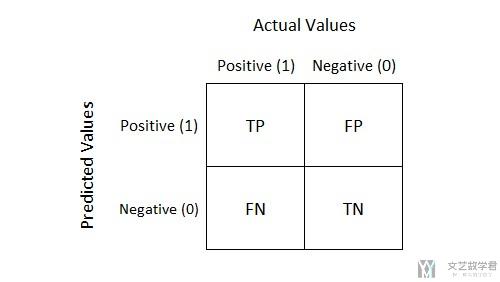
我们简单使用文字来描述一下上面不同状态的含义。

• TP: 预测为1(Positive)，实际也为1(Truth-预测对了)
• TN: 预测为0(Negative)，实际也为0(Truth-预测对了)
• FP: 预测为1(Positive)，实际为0，也就是 Negative(False-预测错了)
• FN: 预测为0(Negative)，实际为1，也就是 Positive(False-预测错了)

我们通过一个例子来看一下上面四个状态是什么意思。我们使用怀孕的例子进行类比。

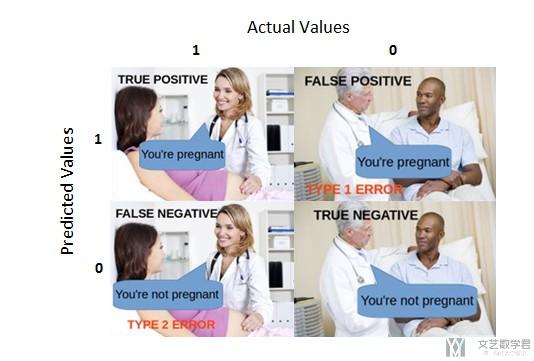
我们结合上面的例子重新解释一下这四种不同的状态的含义。

True Positive:

• Interpretation: You predicted positive and it's true.
• You predicted that a woman is pregnant and she actually is.

True Negative:

• Interpretation: You predicted negative and it's true.
• You predicted that a man is not pregnant and he actually is not.

False Positive: (Type 1 Error)

• Interpretation: You predicted positive and it's false.
• You predicted that a man is pregnant but he actually is not.

False Negative: (Type 2 Error)

• Interpretation: You predicted negative and it's false.
• You predicted that a woman is not pregnant but she actually is.

对于上面的True/False和Postive/Negative, 我们只需要记住我们在描述实际值的时候, 使用True/False, 我们在描述预测值的时候, 我们会使用Postive/Negative.

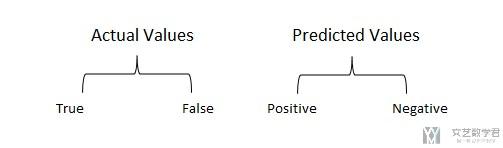
下面我们来理解一下Accuracy, Precision, Recall三者的含义和如何计算的。

一些衍生的指标--FPR, FNR, FAR

The false alarm rate (FAR) is the average ratio of themisclassified to classified records either normal or abnormal as denoted in Eq. (22)(下面的等式).

It is designed from Eqs. (20) and (21) to calculate the false positive rate (FPR) and the false negative rate (FNR), respectively.

Accuracy/Precision/Recall的定义

下面这张图片能解释得很清楚，先放这张图片。

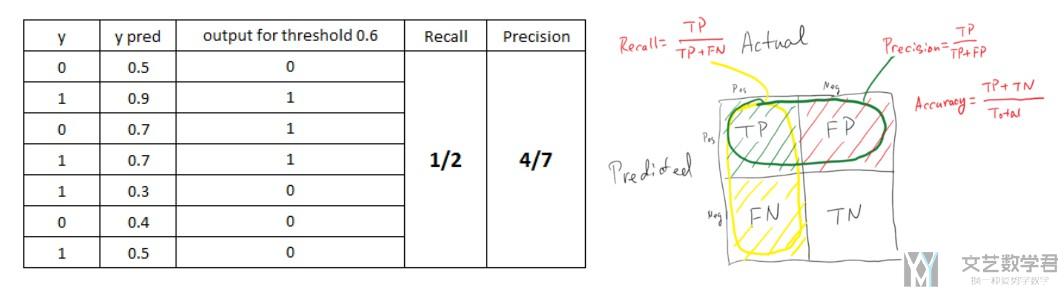
• 对于上面图片的情况来说:
  • TP=2
  • FP=1
  • FN=2
  • TN=2
• Accuracy = (预测正确的样本数)/(总样本数)=(TP+TN)/(TP+TN+FP+FN)
• Precision = (预测为1且正确预测的样本数)/(所有预测为1的样本数) = TP/(TP+FP), 这个值也是越大越好, 上面例子的计算是2/3, 上面图片好像是错的。
• Recall = (预测为1且正确预测的样本数)/(所有真实情况为1的样本数) = TP/(TP+FN), 这个值是越大越好, 上面得例子中是2/4=0.5

F1值

由于Precision/Recall是两个值，无法根据两个值来对比模型的好坏。有没有一个值能综合Precision/Recall呢？有，它就是F1值.

他的计算如下所示：

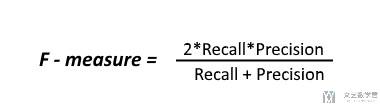
• F1 = 2*(Precision*Recall)/(Precision+Recall)

Micro Average vs Macro average

在多分类的时候，我们还会计算Micro Average和Macro average这两个值。下面简单说明一下这两个值是如何进行计算的。

参考链接 : Micro Average vs Macro average Performance in a Multiclass classification setting

A macro-average will compute the metric independently for each class and then take the average (hence treating all classes equally).(macro-average相当于是对所有分类的指标进行平均)

A micro-average will aggregate the contributions of all classes to compute the average metric.(micro-average有点类似与加权平均, 他会考虑每个类的样本的个数, 在面对每一类数据量不平衡的时候会起到作用)

下面我们来看一个例子，计算macro-average Precision 和micro-average Precision.

现在有四个类别, 分别是A,B,C,D, 他们的TP和FP分别如下所示 :

• Class A : 1 TP and 1 FP
• Class B : 10 TP and 90 FP
• Class C : 1 TP and 1 FP
• Class D : 1 TP and 1 FP

我们分别计算每个类别的Precision, 结果如下所示 :

Class A, Class C, Class D的Precision是一样的, 都是0.5.

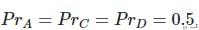
Class B的Precision是0.1.

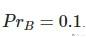
那么，我们就可以计算macro-average Precision 和micro-average Precision. 计算的式子如下所示：

• A macro-average will then compute(就是每一类的Pr求平均):

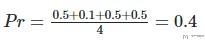
• A micro-average will compute(这个会根据样本的个数重新进行计算):

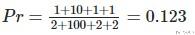
对于weighted avg的计算, 其实就是考虑每个类中正确分类样本个数, 来对原始的值进行加权, 我们在后面讲简单实践的时候给出具体的计算的过程.

简单的实践

上面说完一些指标的含义，下面简单介绍一下如何实际来计算指标。其实这些都不用我们自己来实现，我们可以直接使用。下面是一段可以直接使用的代码。

代码链接 : model_evaluation_utils

上面的代码可能由于时间问题, 在最新的版本存在一些问题, 我将其修改之后上传了github: 模型评价与混淆矩阵的绘制

我们将上面的代码保存到文件中，就可以直接进行使用。如将其保存为tool.py的文件，我们可以使用下面的方式进行调用。

关于具体的实现, 实际是调用了sklearn.metrics.classification_report, 说明文档如下：

sklearn说明文档 : sklearn.metrics.classification_report

下面简单看一下使用的方式。

最终的显示结果如下(在这里我就简单做一下演示, 就用之前做的实验的一个截图放在这里)：

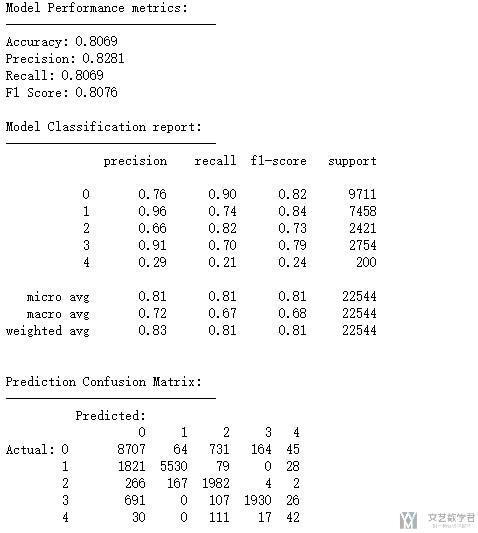
下面我们来一一计算(解释)一下上面的各项的值是如何计算出来的. 我们重新写一下上面的混淆矩阵, 为了方便我们后面的计算.

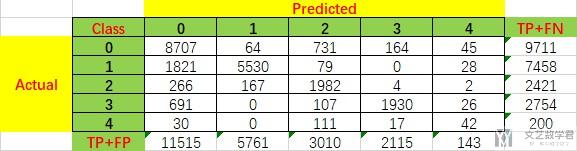
我们首先计算Precision和Recall, 我们只计算class0类(即Normal类)的两个指标。

我们接着计算一下Normal的F1值，如下所示：

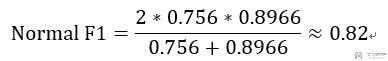
下面我们计算一下macro-average Precision 和micro-average Precision和weight-average的值. 计算过程如下。

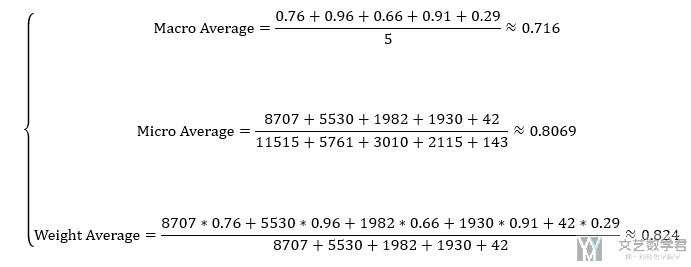
可以看到计算得到的值与上面使用sklearn计算得到的值是一样的。