機器學習基石上 (Machine Learning Foundations)—Mathematical Foundations

简介

自己最近在看林軒田老师的<機器學習基石上>这门课, 就在这里记录一下. 因为已经有人做了详细的记录, 我就这里就直接记录一下参考链接, 和我觉得一些补充的内容.

我自己是在coursera上进行学习的, 里面会有讨论组在讨论相关的问题. 機器學習基石上

课程内容

第一周课程内容-机器学习的定义

第一周给出了一个机器学习的定义, 可以简单分为四个部分.

• 什么是机器学习
• 机器学习的应用
• 机器学习的整体流程(这里有一个整体的流程图, 里面的概念之后会经常使用到)
• 机器学习与其他领域的关系

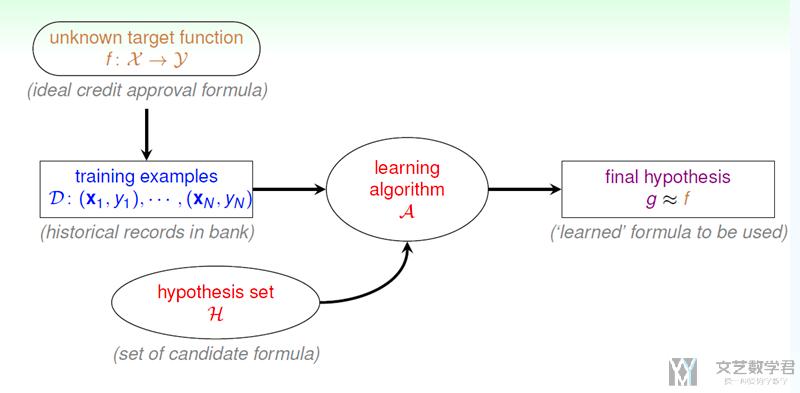
机器学习的目标是: 根据training examples, 通过learning algorithm从hypothesis set中找出一个最好的g, 使得g与f是接近的.

第一周笔记(PLA之前都是第一周的, 后面是第二周的): Coursera台大机器学习基础课程学习笔记1 -- 机器学习定义及PLA算法

第二周课程内容-解决是非问题(线性分类器)

我自己感觉第二周的内容是其实可以理解为对第一周的整体流程给出了一个详细的例子. 对其中每一个概念给出一个详细的例子. 第二周的内容也是可以分为四个部分.

• 当上面hypothesis set是线性分类器的情况
• 通过(learning algorithm), 这里介绍的是PLA, 来找出hypothesis set中最优的解.
• 证明PLA算法在data是线性可分的情况下一定是可以收敛的. (在这一部分的内容里, 课件里面没有给出PLA收敛的后续的详细的说明, 具体可以参考一下下面的笔记.)
• 简单修正PLA算法, 可以处理线性不可分情况.

下面是详细的例子来对第一周的内容进行说明, 主要看一下hypothesis set和learning algorithm是什么.

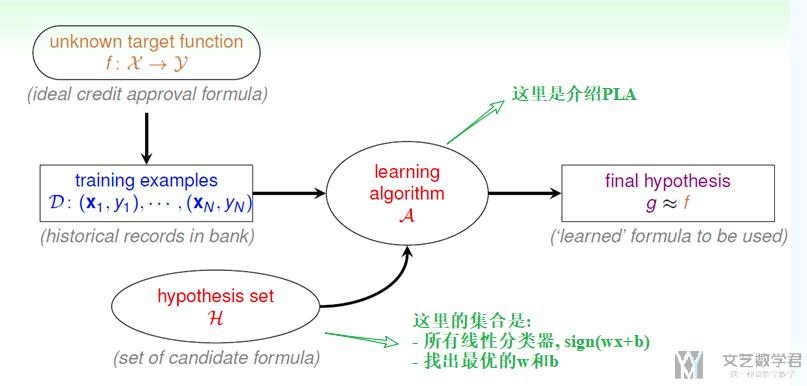
第二周笔记(PLA之后是第二周的): Coursera台大机器学习基础课程学习笔记1 -- 机器学习定义及PLA算法

第三周课程内容-机器学习的分类

第三周的内容是按照不同的角度对机器学习进行分类, 我觉得这一周的课时还是很有启发性的. 这一部分还是分为四部分来介绍.

• 按照output space分类
  • 多分类问题(multiclass classification)
  • 回归问题(regression), 这里output是属于(lower, upper)
  • 结构化问题(structure), 这里input可能是一段(一个句子), output是与输入的结构有关(如这个句子中每个词的词性, 这里不是一个多分类问题, 因为要把词放在句子里才有词性)
• 按照data label分类
  • 监督学习(supervised), 有data和label
  • 无监督学习(unsupervised), 只有data, 没有label
  • 半监督学习, 少量的数据有label, 但是大部分数据没有label
  • 强化学习, 有的时候很难评价这一步是好还是不好, 要看一个整体的过程. 或者需要不同的有反馈来进行学习.
• 按照protocol分类(这个是按照训练方式来分类)
  • batch训练, 每次以一个batch进行输入
  • online训练, 是以序列进行输入, 例如现在有x, 根据g(x)=y', 得到反馈实际是y, 则对g进行修正. (例如强化学习)
  • active训练(active learning), 机器也可以主动提出问题. 例如机器可以提出某个x, 说不知道对应的y是什么(可能是没有得到很高的概率), 我们给出对应的解答
• 按照input space分类
  • 具体特征(concrete feature), 人们根据自己的经验提取的特征. 这些是有实际的意义的. 例如做硬币的分类, 根据硬币的重量和大小.
  • 原始特征(raw feature), 例如图像分类, 输入就是图像, 这里图像就是原始特征. (我们通过特征工程等方式, 将原始特征转换为具体特征.)
  • 抽象特征(abstract feature), 抽象特征例如用户id或是物品id, 这些特征没有实际的意义. 例如某个用户id给物品id打A分, 我们要预测这个用户给其他的打分. (我们通过某些方式, 将抽象特征转换为具体特征)

第三周笔记: Coursera台大机器学习基础课程学习笔记2 -- 机器学习的分类

第四周课程内容-机器学习的可能性(Feasibility of Learning)

第四周的内容是讨论机器学习(也就是learning)的可行性, 即是否可以做到.

首先讨论learning是否是可以做到的. 如果做不到, 是否可以通过增加一些限制, 使其可以做到. 例如有下面的一个例子, 输入是一个三维的向量, 每个值只能取0或者1两个值. 现在target function是f, 现在要找一个g, 使得f≈g.

如下图所示, 我们可以找到一个g, 在训练集D上, g的预测值和观测值y全部一样. 但是对于没出现在训练集的数据, g没法做出预测, 因为target function可能是f1到f8中的任何一种可能.

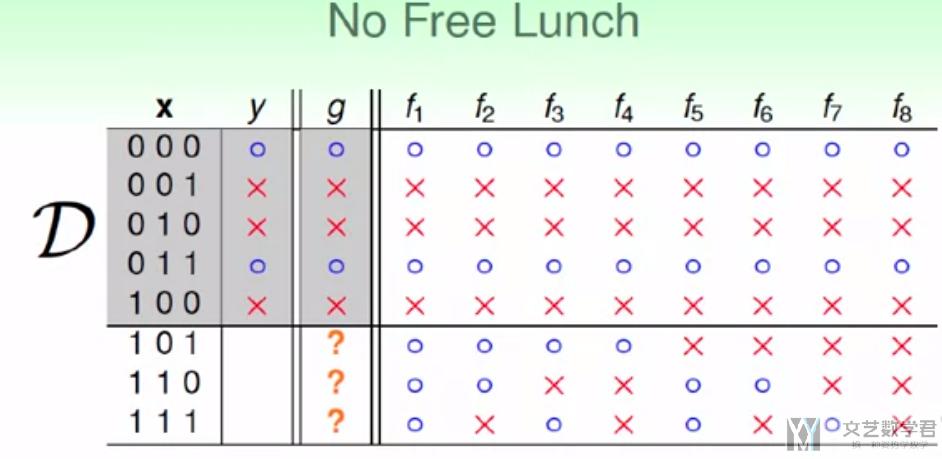
也就是, 如果没有任何的假设或是限制, 在训练集D以外的数据, 我们通常是得不到任何结论的, 也就是我们无法做到learning, 无法学习到训练集以外的东西.

上面我们无法直接推测出D以外的内容, 那么我们是否可以得到一些别的推论呢. 这里我们需要首先介绍hoeffding inequality (霍夫丁不等式), 如下图所示:

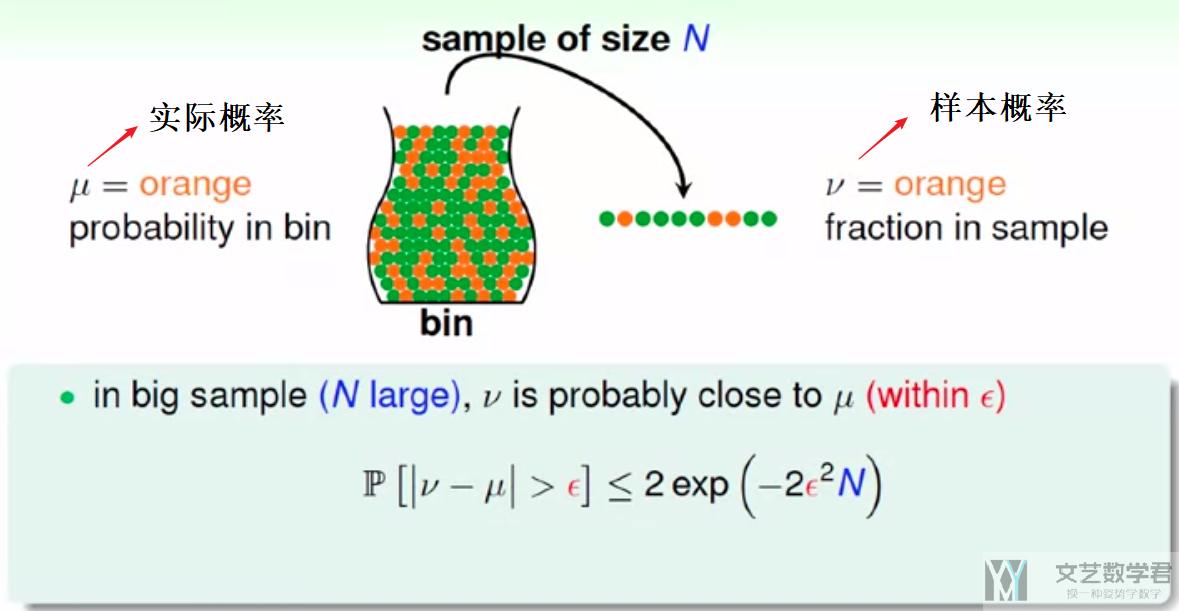
我们使用瓶子里装彩球来作为例子, 现在瓶中橙色球的实际比例是μ, 我们抽样一组, 其中样本中橙色球的比例是v, 于是(μ-v)的满足hoeffding inequality (霍夫丁不等式). 也就是当抽样的样本个数N越大, v与μ接近的概率越大(PAC, probably approximately correct).

下面我们将上面的内容与learning联系起来. 现在假设:

• 我们的target function f(x), f(x)我们是不知道的
• fixed hypothesis h(x) (从可能的集合中找到一个可能的解)
• 所有数据我们称为X(相当于上面罐子中的所有的球)
  • 如果h(x)=f(x), 即预测正确, 我们类比为上面罐子中的橙球;
  • 如果h(x)≠f(x), 即预测错误, 我们类比为上面罐子中的绿球;
• 那么在训练集D(D是X的子集, 相当于我们在X中进行了抽样, 这里需要保证D和X是有一个分布产生的, 也就是对罐子里的球进行了抽样)上, 我们可以有h(x)的准确率, 相当于罐子中橙色球所占比例.
• 于是, 当样本个数足够多(也就是训练集足够大的时候), h(x)在D上的准确率和在X上的准确率有很大概率是相近的.

这个也就保证了在learning过程中, 我们如果保证在D上准确率高, 那么h(x)在X上的准确率也是高的. 我们定义在D(训练集)上的误差为E_in, 在整个X上的误差为E_out.

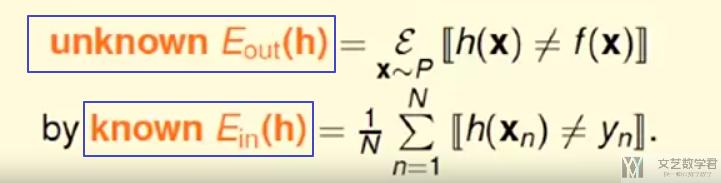
当N足够大的时候, E_in和E_out很大程度上接近, 当E_in很小的时候, 此时g=h与f也是接近的.

上面讲了在给定一个h的情况下, 我们可以通过去验证这个h的好坏. 如果有很多h的时候, 如果其中有一个的E_in很小, 我们是否可以认为这个h是最优的呢, 即是否选择这个h, 来使得g=h呢.

其实这是不一定的, 例如现在有1个人, 连续投掷5次硬币, 5次都朝上的概率是1/32; 但是现在有150个人, 其中有一个人五次都朝上的概率是1-(31/32)^150=0.99. 这个时候出现1个人5次都朝上的概率就会很大.

放在learning的时候, 因为会有许多不同的h, 则出现E_in很小但是E_out很大的概率也会变多. 也就是下图所示, 横轴表示不同的h, 纵轴表示在不同的数据集中进行测试.

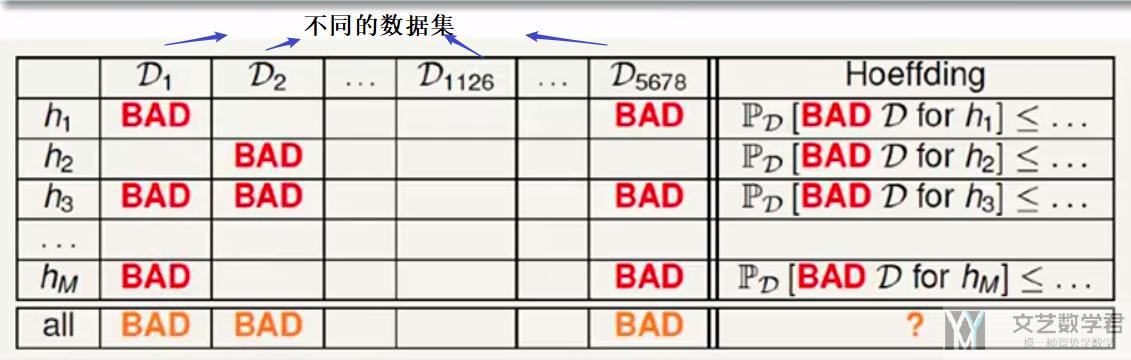
首先看一行, 可以看到h只会在少数的训练集D上表现不好, 大部分训练集D是表现好的. 这些坏训练集D出现的概率的满足hoeffding inequality (霍夫丁不等式). 但是我们很多行一起看, 因为会有很多的h, 只要该训练集D在一个h上表现不好, 那么这个训练集D就是不好的.

例如在D_1这一列, h_1和h_3在D_1上面会出现E_in很小但是E_out很大, 此时根据E_in最小选出的h就不一定是最好的, 可能只是在这个数据集上表现比较好.

现在我们认为只要在一个h上是坏训练集, 那么这个D就是坏训练集, 此时出现的概率如下所示:

可以看到此时出现概率于M(h的个数)和N(训练集样本个数)有关. 当M有限的时候, N足够大, 我们就说可以找到h, 使得E_in和E_out是接近的. 于是在实际做的时候, 我们会选择一个E_in最小的h.

于是现在, 整体的流程如下所示, 这里多了我们可以控制训练集D从一个分布产生, 同时对于h, 我们可以使用相同的方式抽样来进行检测.

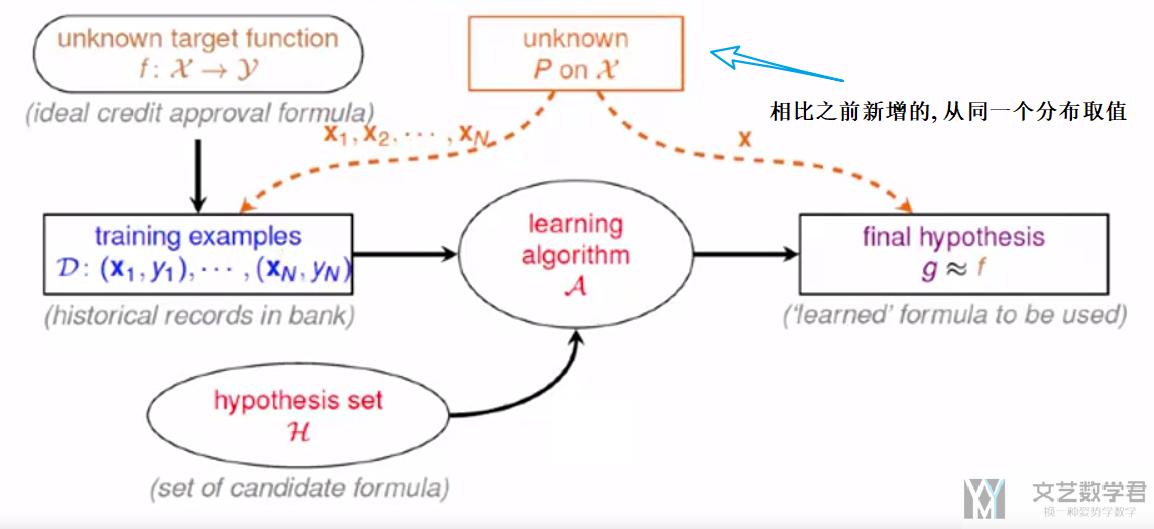
但是实际情况是M是无限的, 无限的情况我们会在后面一部分介绍.

第四周笔记参考资料: Coursera台大机器学习课程笔记3 – 机器学习的可能性