文章目录(Table of Contents)
简介
这一篇主要介绍熵(Entropy), 交叉熵(Cross-Entropy), 和KL散度(KL-Divergence), 这个也是我无意中看到的一个视频, 讲得非常好, 所以我就将其分解的讲一下.
原始视频链接: https://www.youtube.com/watch?v=ErfnhcEV1O8. 下面是视频的封面。

关于在PyTorch中CrossEntropyLoss的实际计算, 我单独写了一篇文章进行详细的介绍, PyTorch中交叉熵的计算-CrossEntropyLoss介绍. 这里给了具体的例子, 有了predict和target之后是如何计算loss的.
熵(Entropy)的介绍
我们以天气预报为例子, 进行熵的介绍.
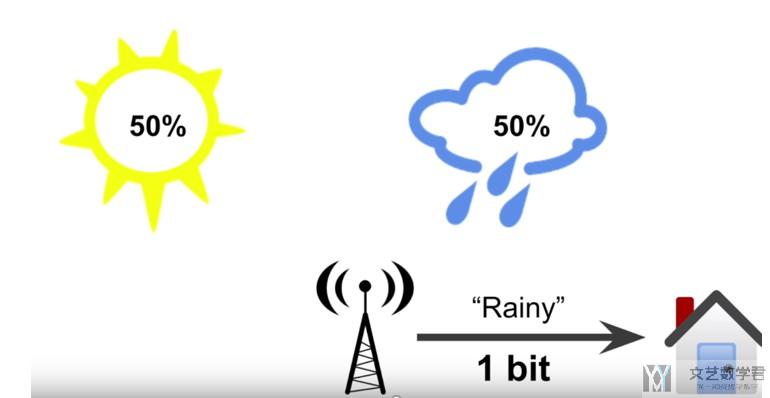
- 假如只有2种天气, sunny 和 rainy, 那么明天对于每一种天气来说, 各有50%的可能性.
- 此时气象部门告诉你明天是rainy, 他其实减少了你的不确定信息.
- 所以, 天气部门给了你1 bit的有效信息(因为此时只有两种可能性).
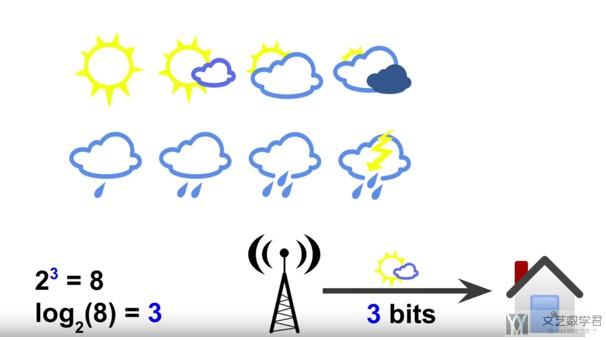
- 假如只有8种天气, 每一种天气出现是等可能的.
- 此时气象部门告诉你明天是Rainy, 他其实减少了你的不确定信息, 也就是告诉了你有效信息.
- 所以, 天气部门给了你3 bit的有效信息(因为8中状态需要 2^3=8, 需要3 bit来表示.
- 所以, 有效信息的计算可以使用log来进行计算, 计算过程如下
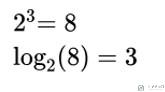
- 上面所有的情况都是等概率出现的, 假设各种情况出现的概率不是相等的.
- 例如有75%的可能性是Sunny, 25%的可能性是Rainy.
- 如果气象部门告诉你明天是Rainy
- 我们会使用概率的倒数, 1/0.25=4 (概率越小, 有效信息越多)
- 接着计算有效信息, log2(1/0.25)=2=(-log2(0.25), log的等价计算)
- 因为和本来的概率相差比较大, 所以获得的有效信息比较多(本来是Rainy的可能性小)
- 如果气象部门告诉你明天是Sunny
- 同样计算此时的有效信息, log2(1/0.75)=-log2(0.75)=0.41
- 因为和本来的概率相差比较小, 所以获得的信息比较少(本来是Sunny的可能性大)
- 从气象部门获得的信息的平均值(这个就是熵)
- 75%*0.41+25%*2=0.81
- 简单解释: 有75%的可能性是Sunny, 得到晴天的有效信息是0.41, 所以是0.75*0.41
- 于是我们得到了熵的计算公式.
- 熵是用来衡量获取的信息的平均值, 没有获取什么信息量, 则Entropy接近0.
- 下面是熵的计算公式
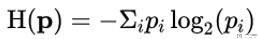
交叉熵(Cross-Entropy)的介绍
对于交叉熵的介绍, 我们还是以天气预报作为例子来进行讲解.
- 交叉熵(Cross-Entropy)可以理解为平均的message length, 即平均信息长度.
- 现在有8种天气, 于是每一种天气我们可以使用3 bit来进行表示(每一种天气的表示方式如下图所示).
- 此时 average message length=3, 所以此时Cross-Entropy=3
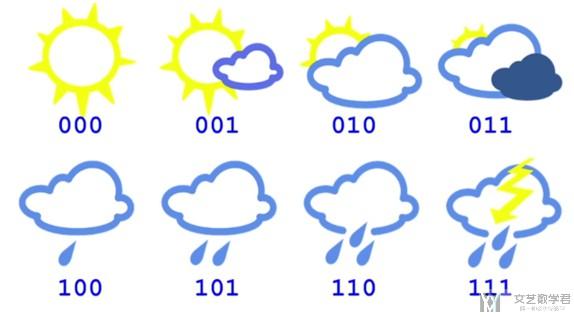
现在假设你住在一个sunny region, 出现晴天的可能性比较大(即每一种天气不是等可能出现的), 下图是每一种天气的概率.
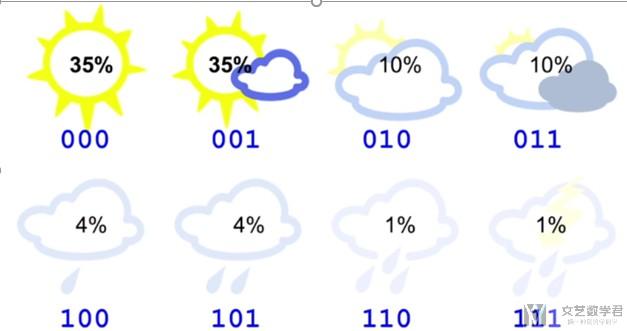
我们来计算一下此时的熵(Entropy), 计算的式子如下所示:
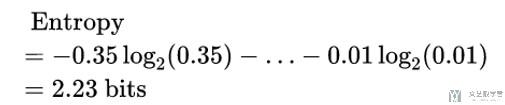
- 此时有效的信息是2.23 bit.
- 所以再使用上面的编码方式(都使用3 bit)会有冗余.
- 也就是说我们每次发出3 bit, 接收者有效信息为2.23 bit.
- 这时我们可以修改天气的encode的方式, 可以给经常出现的天气比较小的code来进行表示, 于是我们可以按照下图对每一种天气进行encode.
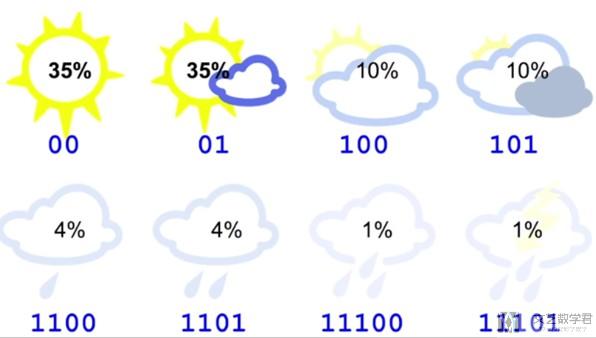
此时的平均长度的计算如下所示(每一种天气的概率*该天气code的长度):
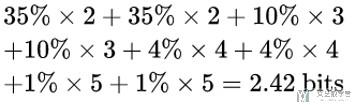
此时的平均长度为2.42bit, 可以看到比一开始的3 bit有所减少.
如果我们使用相同的code, 但是此时对应的天气的概率是不相同的, 此时计算出的平均长度就会发生改变. 此时每一种天气的概率如下图所示:

于是此时的信息的平均长度就是4.58bit, 比Entropy大很多 (如上图所示, 我们给了概率很小的天气的code也很小, 概率很大的天气的code也很大, 此时就会导致计算出的平均长度很大), 下面是平均长度的计算的式子.
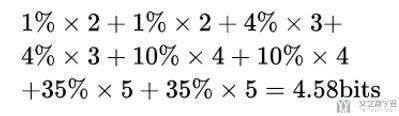
我们如何来理解我们给每一种天气的code呢, 其实我们可以理解为这就是我们对每一种天气发生的可能性的预测, 我们会给出现概率比较大的天气比较短的code, 这里的概率是我们假设的, 即我们有一个估计的概率, 我们估计这个天气的概率比较大, 所以给这个天气比较短的code.
下图中可以表示出我们预测的q(predicted distribution)和真实分布p(true distribution). 可以看到此时我们的预测概率q与真实分布p之间相差很大(此时计算出的交叉熵就会比较大).

关于上面code长度与概率的转换, 我们可以这么来进行理解, 对于概率为p的信息, 他的有效信息为-log2(p). 若此时code长度为n, 我们问概率为多少的信息的有效信息为n, 即求解-log2(p)=n, 则p=1/2^n, 所以我们就可以求出code长度与概率的转换.
此时, 我们就可以定义交叉熵(Cross-Entropy), 这里会有两个变量, 分别是p(真实的分布)和q(预测的概率):
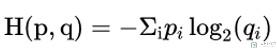
这个交叉熵公式的意思就是在计算消息的平均长度, 我们可以这样来进行理解.
- -log2(q)是将预测概率转换为code的长度(这里看上面code长度与概率的转换)
- 接着我们再将code的长度(-log2(q))乘上出现的概率p(真实的概率)
我们简单说明一下熵(Entropy),和交叉熵(Cross-Entropy)的性质:
- 如果预测结果是好的, 那么p和q的分布是相似的, 此时Cross-Entropy与Entropy是相似的.
- 如果p和q有很大的不同, 那么Cross-Entropy会比Entropy大.
- 其中Cross-Entropy比Entropy大的部分, 我们称为relative entropy, 或是Kullback-Leibler Divergence(KL Divergence), 这个就是KL-散度, 我们会在后面进行详细的介绍.
- 也就是说, 三者的关系为: Cross-Entropy=Entropy+ KL Divergence
交叉熵(Cross-Entropy)在机器学习中的应用
在进行分类问题的时候, 我们通常会将loss函数设置为交叉熵(Cross-Entropy), 其实现在来看这个也是很好理解, 我们会有我们预测的概率q和实际的概率p, 若p和q相似, 则交叉熵小, 若p和q不相似, 则交叉熵大.
有一个要注意的是, 我们通常在使用的时候会使用10为底的log, 但是这个我不影响, 因为log2(x)=log10(x)/log(2), 我们可以通过公式进行转换.
我们下面来看一个例子, 在实际情况中的使用.
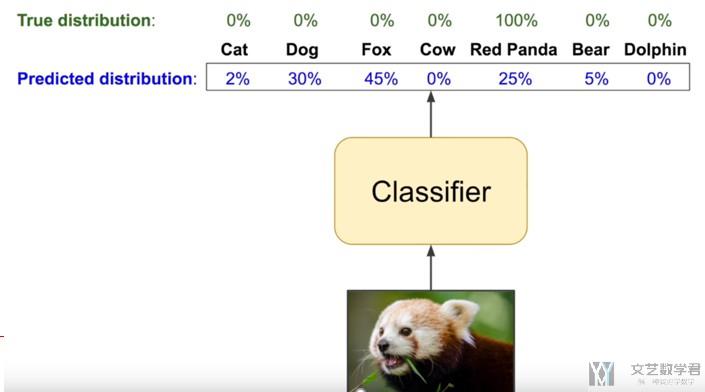
若预测Red Panda为90%, 则Cross-Entropy为0.04.
若预测Red Panda为100%, 则Cross-Entropy为0.
注意: 不是交叉熵越接近0越好, 应该是KL-Divergence越接近0越好. 但是在这里, 多分类使用one-hot表示正好导致了正确结果的时候Cross-Entropy为0.
在PyTorch中, CrossEntropyLoss不是直接按照上面进行计算的, 他是包含了Softmax的步骤的. 关于在PyTorch中CrossEntropyLoss的实际计算, 我单独写了一篇文章进行详细的介绍, PyTorch中交叉熵的计算-CrossEntropyLoss介绍. 这里给了具体的例子, 有了predict和target之后是如何计算loss的.
KL散度(KL-Divergence)
- 前面说到, 三者的关系为: Cross-Entropy=Entropy+ KL Divergence
- 所以, KL-Divergence的计算式子如下所示:
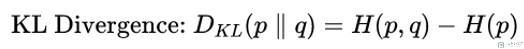
我们计算一下上面那个天气的KL-Divergence, 下面是天气的真实概率分布, 和我们预测的概率分布:

于是KL-Divergence的计算结果如下:
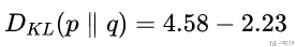
下面是一些更加数学化的表示, 分别看一下离散概率分布和连续概率分布下的公式. 我们知道KL-Divergence的计算公式如下所示:
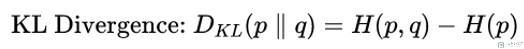
我们将熵和交叉熵的计算公式代入, 进行化简, 于是得到了下面的式子, 其中p是真实的概率分布, q是我们预测的概率分布.

我们看一下离散情况下的详细计算公式:
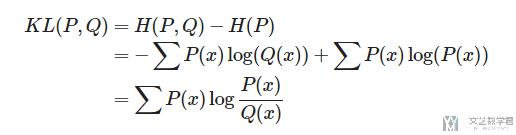
参考资料: https://zhuanlan.zhihu.com/p/22464760
KL-Divergence简单例子
下面我们来看一个简单的KL-Divergence的例子(需要注意的是, KL不是对称的, 即KL(P||Q)!=KL(Q||P)). 假设P和Q为离散部分, 如下所示:
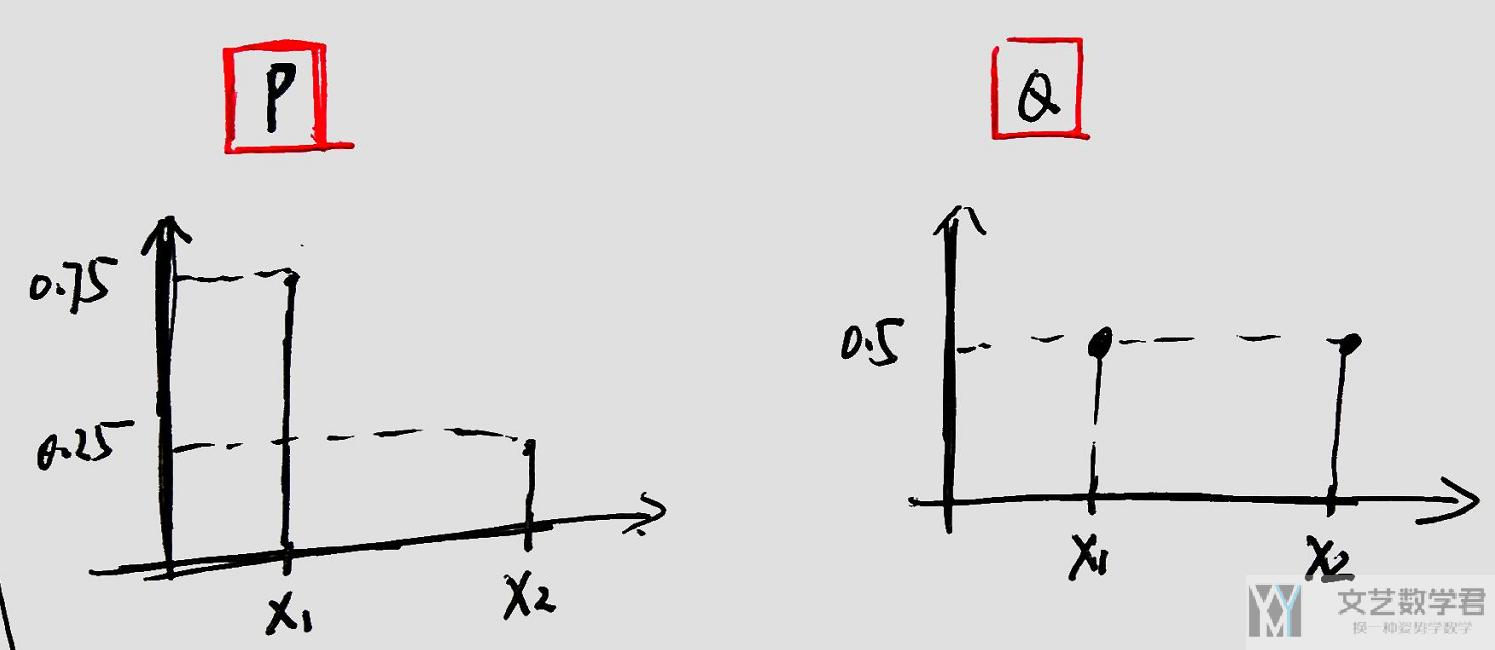
那么此时的KL(P,Q)和KL(Q,P)的计算分别如下:
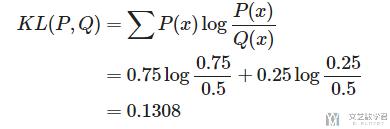
下面是KL(Q,P)的计算
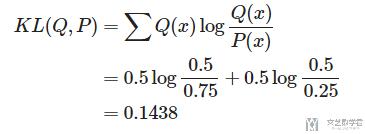
可以看到两者的结果是不同的.
KL散度(KL-Divergence)-算例(计算两个高斯分布的KL-Divergence)
- 这里我们看一下对于两个一维的高斯分布, 我们计算他们之间的KL-Divergence.
- 假设有两个随机变量x1和x2, 各服从如下的高斯分布:
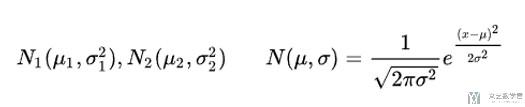
下面计算KL(p1||p2), 将正态分布的概率密度函数代入计算, 下面的计算过程就截图表示:

我们进一步进行化简:
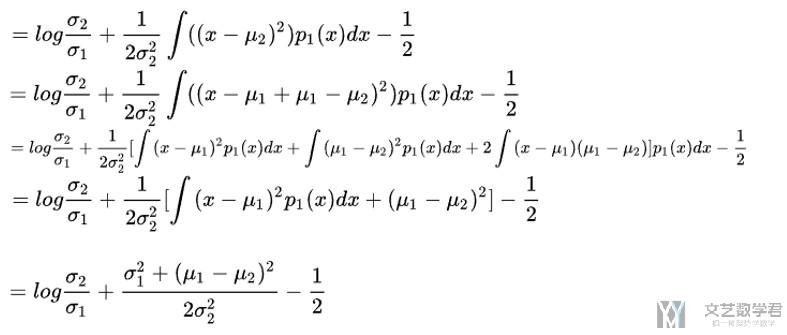
我们看一下是否是KL-Divergence越小, 表示两个分布越接近.
如果我们假设第二个高斯分布的均值为0, 方差为1(这里假设N2是均值是0和方差是1的正态分布), 那么此时的KL-Divergence可以化简为如下的式子.
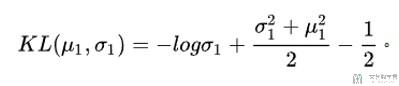
我们可以猜测此时, 均值为0, 方差为1的时候KL散度最小, 会使得KL-Divergence=0. 我们可以求导进行验证.
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-












评论