文章目录(Table of Contents)
简介
这一篇会详细推导一下Logistic Regression中的损失函数的由来, 也是可以从一个角度看一下交叉熵的由来.
关于在PyTorch中CrossEntropyLoss的实际计算, 我单独写了一篇文章进行详细的介绍, PyTorch中交叉熵的计算-CrossEntropyLoss介绍. 这里给了具体的例子, 有了predict和target之后是如何计算loss的.
例子引入
要介绍分类问题,我们从最基本的想法进行出发。
- 现在有两个Box, 里面装有一些圆和三角(个数如下图所示).
- 抽到Box1的概率为2/3,抽到Box2的概率为1/3.
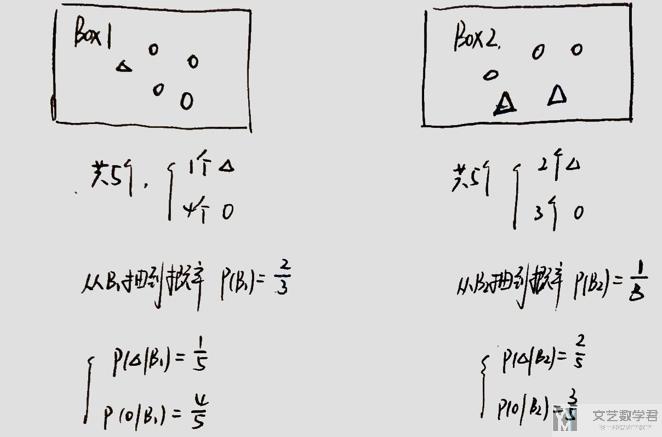
此时,若我们抽到一个三角,问这个三角是来自Box1还是Box2. 对于这个问题,我们可以使用贝叶斯公式进行求解。(关于贝叶斯公式的例子,也可以看一下这个链接,贝叶斯公式与全概率公式的应用–一道面试题)

我们如果将上面的Box1和Box2看成两个类,分别是Class1和Class2,于是就变成了一个分类的问题了。
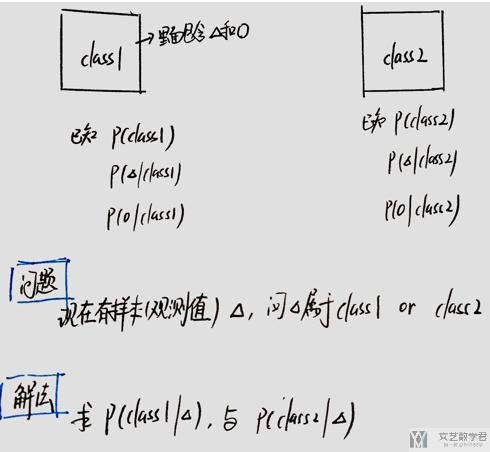
如果我们抽到的是三角,我们只需要计算P(class1|三角) 和P(class2|三角)的概率大小进行比较即可。
我们总结一下上面所讲的内容,我们发现现在要求一个观测值的分类问题,就是要解出那个贝叶斯的式子的值,再具体一些就是四个概率的值。
即求下面的式子,也就是求出P(c1), P(c2), P(x|c1), P(x|c2)这四个值。
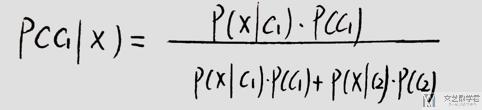
下面会讲两个解法,分别是generative model和logistic regression.
Generative Model
Generative Model的想法就是求出上面式子中四个概率的值。
P(c1)和P(c2)的计算
P(c1)和P(c2)的计算没什么难度,可以直接进行计算.

P(x|c1)和P(x|c2)的计算
关于P(x|c1)和P(x|c2)的计算,分为两种情况,即x是连续变量还是离散变量。
若x是离散的量,我们还是可以直接从样本中计算得到P(x|c1)和P(x|c2),即上面Box的例子。
若x是连续的量,我们就不能使用这种方式进行求解了。例如人的身高是在150-200cm之间的量,我们的样本中有190cm,191cm的人,若此时观测值是190.5cm, 我们不能说这个概率是0(样本中没有190.5这样的人). 所以一般的做法是,我们会假设x服从高斯分布,从而使用极大似然估计求出这个分布的均值与方差。=> 这里假设变量服从高斯分布是一个很强的假设
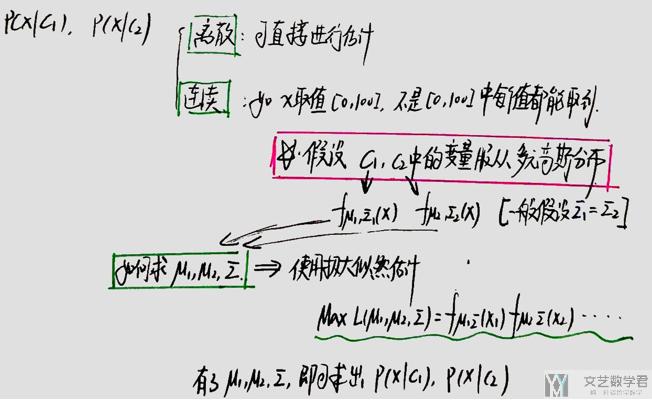
到这里,我们就求出了P(x|c1)和P(x|c2),P(c1)和P(c2),从而就可以计算x在从c1中的概率了。
Logistic Model
下面介绍一下Logistic Model的内容,我们首先看一下他大概的想法,还是从之前的贝叶斯的式子出发,我们可以进行如下的化简。
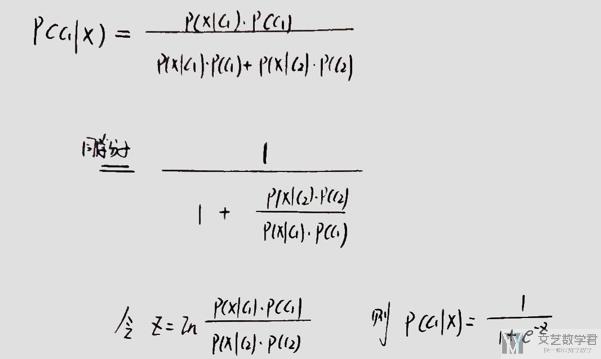
通过上面的化简,我们可以看到P(c1|x)可以等价与一个Sigmoid的表达式,其实下面就是对Z进行化简。其实到这里,我觉得有两种解释都是可以行得通的。
第一种解释 : 我们可以认为Logistic Model需要输出一个概率, 于是我们使用Sigmoid函数做压缩, 把(负无穷, 正无穷)的值压缩到(0,1), 所以z=wx+b
第二种解释 : 第二种解释可能会稍微复杂一些,我们将上面假设的x服从高斯分布,代入z进行化简,同样是可以得到结果的。我把具体的推导放在下面,可以参考着推导一下。

最后可以看到z就是关于x的线性函数。下面的问题转换为如何求解w和b。
求解w与b的值
下面的问题是求解w和b的值,我们知道f(x)输出的其实是x属于c1的概率值,于是我们要求解w和b,也可以使用极大似然估计,使得出现数据集中的分类的可能性最大。如下图的表示。

解释一下最后的一个式子,从数据中x1属于c1,x2属于c2。又f(x)是x属于c1的概率,所以最后相乘的时候是f(x1)(1-f(x2)).
对于上面求极大值,我们可以通过负号转换为求极小值;同时我们可以通过log计算将连乘转换为连加。于是就有了下面的式子。

最后写成那个样子也是为了式子的统一。于是我们就可以通过对最后的那个式子,使用梯度下降法进行求解。(最后的那个函数较 Cross Entropy, 也就是神经网络中常用的那个分类的时候的损失函数)
于是稍微总结一下逻辑回归的内容,下面的几个截图来自下面的网站,里面的内容还是很不错的。
- http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML17_2.html

对于逻辑回归和线性回归,最后梯度下降的值是相同的。
上面讲了二分类的问题,我们推广到多分类的问题中去。
多分类问题求解
关于多分类问题,我们的问题变为求解P(C_i|x), 我们通常会使用softmax函数,整体的步骤其实和二分类问题是类似的。我们先看一下大致的步骤,大致步骤看下面的两个图就足够了。
首先我们还是做线性的回归,求解w1与b1,从而计算得到z1=w1*x+b1, 接着将这个值转换为概率值,转换的方法即使用Softmax,具体做法看下面的图。
我们可以看到最后Softmax之后能保证和为1。最后输出的值可以理解为x属于每一个类的概率值。
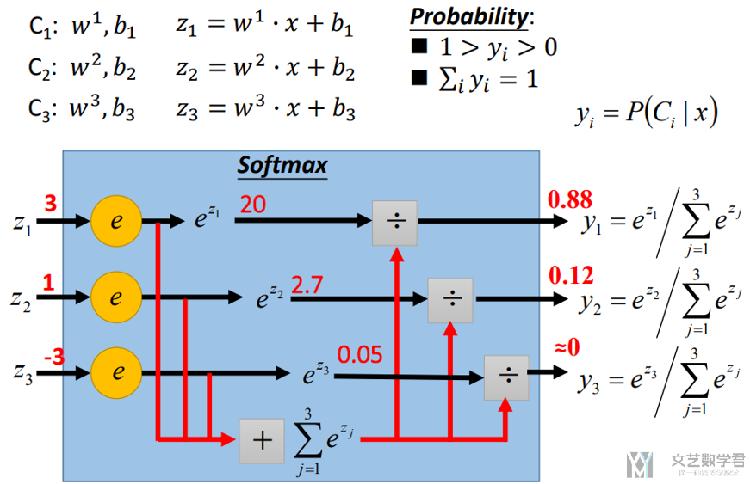
接着,我们要计算损失函数,还是使用交叉熵来进行计算。
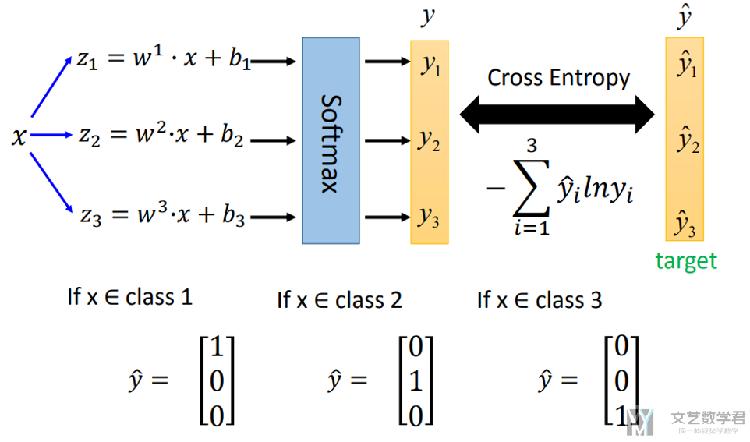
之后,我们就可以使用梯度下降的方法来求解w1,b1等系数了。
关于在PyTorch中CrossEntropyLoss的实际计算, 我单独写了一篇文章进行详细的介绍, PyTorch中交叉熵的计算-CrossEntropyLoss介绍. 这里给了具体的例子, 有了predict和target之后是如何计算loss的.
二分类与多分类的类比
我们说一下二分类与多分类之间的关系。下面这部分是我自己想的,不确定完全正确。
首先是Softmax那部分,如何和二分类联系上。主要是因为二分类,我们只需要比较z1和z2的大小关系即可,即比较z=z1/z2与1的大小关系。

接着是Cross Entropy部分。由于二分类,一定有y1+y2=1,所以一个就可以用另一个表示进行化简了。
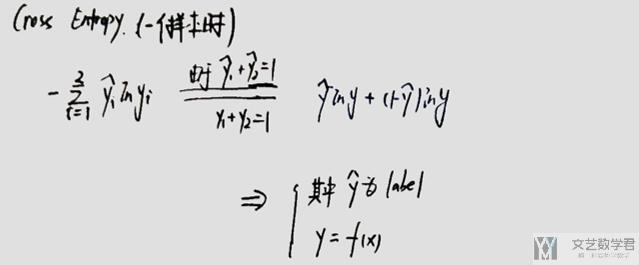
到这里,理论的部分大概是讲完了,大致这么多的内容。下面简单讲一下实际操作,实际的实验。
逻辑回归实验
我就讲一下如何使用吧,其他也没什么。
使用sklearn实现
使用sklearn就很简单了,大致步骤如下。
- from sklearn.linear_model import LogisticRegression
- lr = LogisticRegression(solver='liblinear')
- lr.fit(data.reshape(-1,1), labels.values.squeeze())#进行拟合
- acc = lr.score(data.reshape(-1,1),labels.values.squeeze()) # 进行预测
使用PyTorch实现
网络定义的时候就写一层就可以了,最后的损失函数, CrossEntropyLoss是包含Softmax是,所以就不需要再计算一次Softmax了。
- class NeuralNet(nn.Module):
- def __init__(self, input_size, hidden_size, num_classes, n_layers):
- super(NeuralNet, self).__init__()
- self.LGLayer = nn.Linear(input_size, num_classes)
- def forward(self, x):
- out = self.LGLayer(x)
- return out
- # CrossEntropyLoss里面就包含了softmax的步骤
- criterion = nn.CrossEntropyLoss()
代码链接
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-













评论