正则化技术介绍–L1,L2范数

王茂南

2827
文章

75
评论

2019年4月16日07:18:17

评论 4972字阅读16分34秒

摘要这一篇会简单介绍正则化的技术, 简单介绍一下L1和L2范数的性质, 并记录一下一个实验.

文章目录(Table of Contents)

正则化介绍

当模型过于复杂的时候，可能会出现过拟合的现象，使用正则化技术（Regularization）会减轻过拟合的现象。

正则化简单来说就是在Loss函数中加入系数项，目的是不希望系数太大，从而使得希望模型对于x的变化不会太敏感。

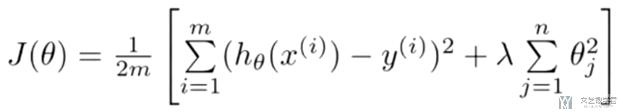
L1,L2范数性质

关于几种范数的介绍，几种范数的简单介绍

首先我们看一下L1，L2范数的性质，后面会有关于这两个性质的说明。

L1范数
- 在使用L1范数时，一些系数会变为0，但是一些系数仍然会比较大;
- 使用L1范数会使得参数变得稀疏(sparse);
- 一种特征提取的方式(嵌入式);
L2范数
- 在使用L2范数时，所有的系数会变得接近0；
L0范数
- L0范数为系数中非零元素的个数；

我们使用一张图片来进行总结：

L1，L2范数在线性回归

对于线性回归来说，如果增加L1，L2正则化分别会对应两种线性回归的方式，分别如下。

L1范数 : LASSO回归
L2范数 : 岭回归

L1范数性质说明

就直接使用拍照的方式了，这些稍微会方便一些。需要注意的是，下面的图片给出了如何使用梯度下降的方式来进行增加了正则化之后模型的求解。

L2范数性质说明

正则化实验

导入库

import numpy as np
import sklearn
from sklearn import model_selection
from matplotlib import pyplot as plt
%matplotlib inline
from sklearn.linear_model import LinearRegression, Lasso, Ridge
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error

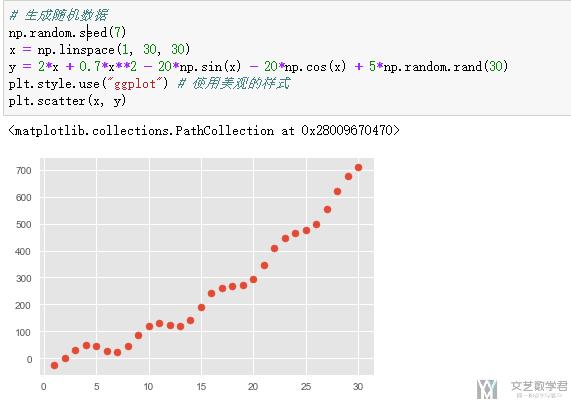
生成实验数据

# 生成随机数据
np.random.seed(7)
x = np.linspace(1, 30, 30)
y = 2*x + 0.7*x**2 - 20*np.sin(x) - 20*np.cos(x) + 5*np.random.rand(30)
plt.style.use("ggplot") # 使用美观的样式
plt.scatter(x, y)

数据做变换

由于在这里我们会使用七次的多项式进行回归，所以我们首先使用PolynomialFeature进行变换;

# 首先将数进行变换
Polynomia_7 = PolynomialFeatures(degree=7)
x_polynomia7 = Polynomia_7.fit_transform(x.reshape(-1,1))

我们看其中一个数据是如何做变换的：

比较使用正则化与不使用正则化

下面我们对上面的实验数据, 分别进行三次实验, 模型分别为不使用正则化技术, 使用L1范数, 使用L2范数. 需要注意的是, 在线性回归中, 如果使用L1范数, 相当于是Lasso回归. 如果使用L2范数, 相当于是Ridge回归, 也就是岭回归. 这些在sklearn中都是可以直接使用的.

# 不使用正则化
model1 = LinearRegression(normalize=True)
model1.fit(x_polynomia7,y)
# 使用L1范数
model2 = Lasso(alpha=1,normalize=True)
model2.fit(x_polynomia7,y)
# 使用L2范数
model3 = Ridge(alpha=1,normalize=True)
model3.fit(x_polynomia7,y)

我们打印一下每一种模型最后的系数:

可以看到使用正则化之后系数变得相对小, 同时使用L1范数，系数中0的个数更多, 使用L2范数, 系数变得接近于0.

接下来我们来看一下三者画出来的最终的结果：

plt.style.use('seaborn')
fig = plt.figure(figsize=(13,7))
ax = fig.add_subplot(1, 1, 1)
model1_pre = model1.predict(x_polynomia7)
model2_pre = model2.predict(x_polynomia7)
model3_pre = model3.predict(x_polynomia7)
plt.scatter(x,y,c='red',label='real') # 画出原图
plt.plot(x,model1_pre,c='green',label='None') # 未使用正则化
plt.plot(x,model2_pre,c='blue',label='L1') # l1范数
plt.plot(x,model3_pre,c='darkviolet',label='L2') # l2范数
plt.legend()

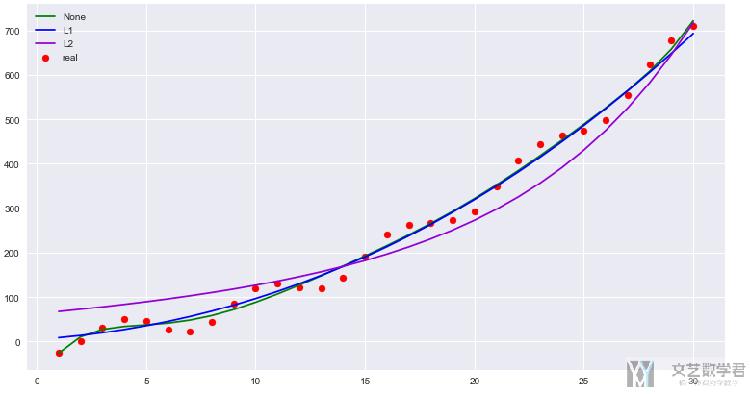
我们查看一下三者模型最后的误差：

# 查看一下三个模型在训练集上的误差
err1 = mean_squared_error(model1_pre,y)
# 计算model2的误差
err2 = mean_squared_error(model2_pre,y)
# 计算model3的误差
err3 = mean_squared_error(model3_pre,y)
print("err1:{:.2f} | err2:{:.2f} | err3:{:.2f}".format(err1,err2,err3))

最终得到的结果为：

err1:348.28 | err2:438.60 | err3:2443.83

不使用正则化技术会在训练集上表现的结果更好（所以说如果在训练集上结果不好时，不需要使用正则化技术）

接着，我们扩大一些预测的范围，看一下三种模型的效果：

x_test = np.linspace(1, 35, 35)
y_test = 2*x_test + 0.7*x_test**2 - 20*np.sin(x_test) - 20*np.cos(x_test) + 5*np.random.rand(35)
x_test_polynomia7 = Polynomia_7.fit_transform(x_test.reshape(-1,1))
plt.style.use('seaborn')
fig = plt.figure(figsize=(13,7))
ax = fig.add_subplot(1, 1, 1)
model1_pre = model1.predict(x_test_polynomia7)
model2_pre = model2.predict(x_test_polynomia7)
model3_pre = model3.predict(x_test_polynomia7)
plt.scatter(x_test,y_test,c='red',label='real') # 画出原图
plt.plot(x_test,model1_pre,c='green',label='None') # 未使用正则化
plt.plot(x_test,model2_pre,c='blue',label='L1') # l1范数
plt.plot(x_test,model3_pre,c='darkviolet',label='L2') # l2范数
plt.legend()

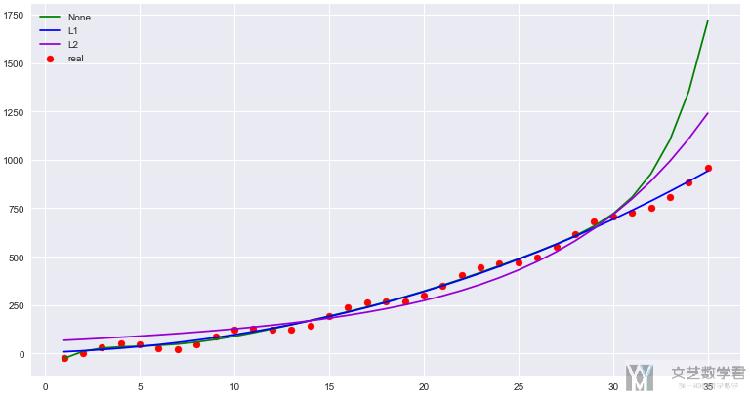
可以看到使用正则化技术之后，模型整体能向外的延拓的效果会更加好一些。

不同惩罚项的影响

下面查看一下不同惩罚系数对于模型的整体的影响。我们使用L1范数，惩罚系数选择0.1, 0.5, 1, 2, 5, 10, 100，最终的效果如下所示：

alpha_list = [0.1,0.5,1,2,5,10,100]
model_list_normalize = [Lasso(alpha=i,normalize=True) for i in alpha_list]
# 分别对上面的模型进行拟合
for model in model_list_normalize:
model.fit(x_polynomia7,y)
# 打印每周模型的参数
for i,model in zip(alpha_list,model_list_normalize):
print("alpha={},coef={}".format(i,model.coef_))
# 计算每种模型的误差并绘图
err_list = []
for model in model_list_normalize:
model_pre = model.predict(x_polynomia7)
model_err = mean_squared_error(model_pre,y)
err_list.append(model_err)
plt.style.use('seaborn')
fig = plt.figure(figsize=(13,7))
ax = fig.add_subplot(1, 1, 1)
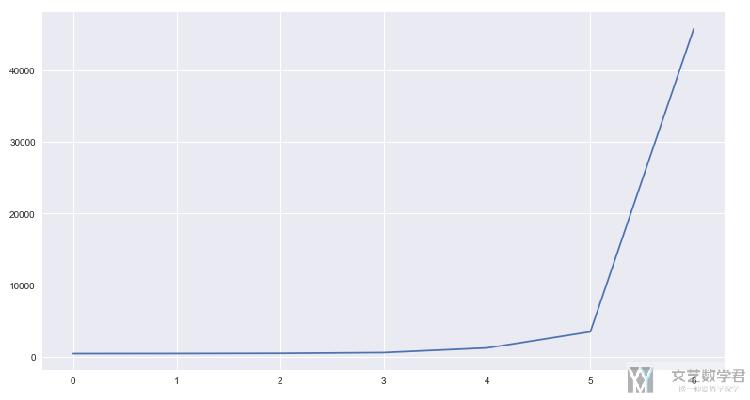
plt.plot(err_list)

首先画出误差的趋势图，可以看到误差随着惩罚系数的增大而增大，这个会是比较好理解的，因为随着惩罚系数的增大，整个的model set在减少。同时，模型会更加区域平稳，最后会变得很平.

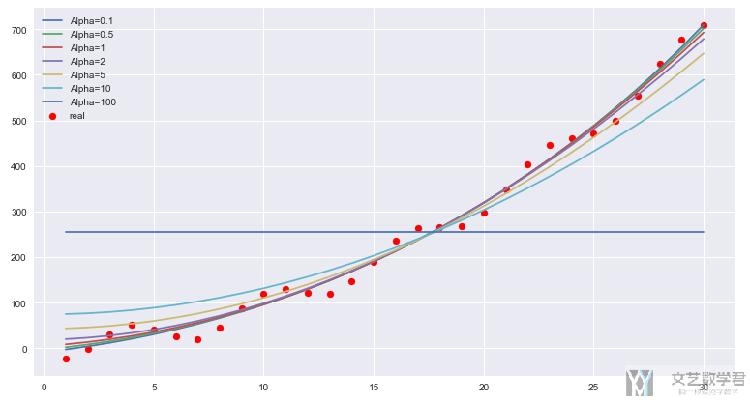
我们画出最终拟合出的直线，可以看到随着惩罚系数的增大，模型整体上在趋于水平；

# 画出不同惩罚项函数的图
# 对模型进行预测
x_test = np.linspace(1, 30, 30)
y_test = 2*x_test + 0.7*x_test**2 - 20*np.sin(x_test) - 20*np.cos(x_test) + 5*np.random.rand(30)
x_test_polynomia7 = Polynomia_7.fit_transform(x_test.reshape(-1,1))
plt.style.use('seaborn')
fig = plt.figure(figsize=(13,7))
ax = fig.add_subplot(1, 1, 1)
plt.scatter(x_test,y_test,c='red',label='real') # 画出原图
for i,model in zip(alpha_list,model_list_normalize):
model_pre = model.predict(x_test_polynomia7)
plt.plot(x_test,model_pre,label='Alpha={}'.format(i)) # 未进行规范化
plt.legend()