Kaggle House Price–一个完整的训练过程

王 茂南
王 茂南
王 茂南
3081
文章
75
评论
2020年9月5日07:56:19
评论 6443字阅读21分28秒
摘要这一篇文章以Kaggle House Price作为例子, 完整的说明一下从数据预处理, 模型构建, 到最后模型选择的一个过程.

简介

这一篇文章会从Kaggle上的房价预测问题来作为例子, 完整的看一下整个的模型的训练流程. 这个训练流程会包括:

  • data preprocessing (数据预处理)
  • model design (模型的构建)
  • hyperparameter selection (使用K-Fold来选择模型)

参考链接

 

Data Preprocessing (数据预处理)

在拿到数据之后, 我们首先要对原始数据进行处理. 这里分为两类数据, 分别是连续型的数据(numerical features), 和离散型的数据(discrete values).

关于这里的数据预处理的操作, 具体的方法可以查看链接, Python科学运算–简单汇总-数据预处理

连续型数据处理

对于连续型的数据, 我们首先对其进行标准化.

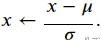
Kaggle House Price–一个完整的训练过程

这样做有两个好处:

  • First, it proves convenient for optimization.
  • Second, because we do not know a priori which features will be relevant, we do not want to penalize coefficients assigned to one variable more than on any other.

连续型数据标准化的代码如下, 同时我们还对缺失数据使用0进行补充.

  1. numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
  2. all_features[numeric_features] = all_features[numeric_features].apply(
  3.     lambda x: (x - x.mean()) / (x.std()))
  4. # After standardizing the data all means vanish, hence we can set missing values to 0
  5. all_features[numeric_features] = all_features[numeric_features].fillna(0)

 

离散型数据处理

接着我们处理离散型的数据. 对于这类数据, 我们将其转换为one-hot encoding的方式. 我们可以直接使用pd.get_dummies来转换为one-hot的数据.

  1. # `Dummy_na=True` refers to a missing value being a legal eigenvalue, and
  2. # creates an indicative feature for it
  3. all_features = pd.get_dummies(all_features, dummy_na=True)

 

划分训练集和测试集

在对数据处理好之后, 我们需要划分训练集和测试集(这里是单独说明一下, 下面是直接取了前n_train的数量作为训练样本, 这里使用一下train_test_split).

  1. from sklearn.model_selection import train_test_split

如果数据保存的格式为dataframe, 那么可以使用下面的方式提取特征和label.

  1. X = df.iloc[:,:-1].values
  2. y = df.class1.values

之后将X和y作为train_test_split的输入即可.

  1. X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.10, random_state= 100)

 

转换为tensor格式

在经过上面对连续数据和离散数据的数据处理之后, 我们将数据转换为tensor的格式, 可以使用Pytorch来进行训练.

  1. n_train = train_data.shape[0] # 训练集样本个数
  2. train_features = torch.tensor(all_features[:n_train].values,
  3.                               dtype=torch.float32)
  4. test_features = torch.tensor(all_features[n_train:].values,
  5.                              dtype=torch.float32)
  6. train_labels = torch.tensor(train_data.SalePrice.values,
  7.                             dtype=torch.float32).reshape(-1, 1)

为了训练更加方便, 我们会将数据存储到dataloader中. 因为上面是tensor的格式, 我们可以直接使用TensorDataset来进行转换.

  1. def load_array(data_arrays, batch_size, is_train=True):
  2.     """Construct a PyTorch data iterator."""
  3.     dataset = data.TensorDataset(*data_arrays)
  4.     return data.DataLoader(dataset, batch_size, shuffle=is_train)

 

Training (开始训练)

上面数据准备完毕之后, 下面就可以开始进行训练.

模型的定义

因为我们在这里只进行简单的说明, 所以我们使用最简单的线性模型来对房价进行预测, 我们使用Pytorch定义一个简单的线性模型.

  1. loss = nn.MSELoss()
  2. in_features = train_features.shape[1]
  4. def get_net():
  5.     net = nn.Sequential(nn.Linear(in_features,1))
  6.     return net

这里定义的模型比较简单, 如果是一些比较复杂的模型, 我们可以使用Pytorch Summary来查看模型的结构, 具体用法可以参考文章, Pytorch模型概览(Pytorch Summary)

 

开始训练

有了模型和损失函数之后, 下面就可以开始训练了. 这里添加的loss用了另外一个. (不过对总体不是很重要) 需要注意的是, 我们在这里进行优化的时候, 还添加了l2的正则化.

  1. def train(net, train_features, train_labels, test_features, test_labels,
  2.           num_epochs, learning_rate, weight_decay, batch_size):
  3.     train_ls, test_ls = [], []
  4.     train_iter = load_array((train_features, train_labels), batch_size)
  5.     # The Adam optimization algorithm is used here
  6.     optimizer = torch.optim.Adam(net.parameters(),
  7.                                  lr = learning_rate,
  8.                                  weight_decay = weight_decay)
  9.     for epoch in range(num_epochs):
  10.         for X, y in train_iter:
  11.             optimizer.zero_grad()
  12.             outputs = net(X)
  13.             l = loss(outputs,y)
  14.             l.backward()
  15.             optimizer.step()
  16.         train_ls.append(log_rmse(net, train_features, train_labels))
  17.         if test_labels is not None:
  18.             test_ls.append(log_rmse(net, test_features, test_labels))
  19.     return train_ls, test_ls

log rmse的计算式子如下所示:

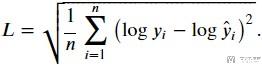
Kaggle House Price–一个完整的训练过程

下面是具体的代码实现.

  1. def log_rmse(net,features,labels):
  2.     # To further stabilize the value when the logarithm is taken, set the
  3.     # value less than 1 as 1
  4.     clipped_preds = torch.clamp(net(features), 1, float('inf'))
  5.     rmse = torch.sqrt(torch.mean(loss(torch.log(clipped_preds),
  6.                                        torch.log(labels))))
  7.     return rmse.item()

 

K-Fold Cross-Validation

这里是用来对模型和超参数进行选择. 关于K-Fold的内容, 可以参考文章, 交叉检验(Cross Validation)简介. 在这里, 为了简单说明, 我们不对模型进行选择, 我们就是给定一个模型的情况下, 用K-Fold的方法, 计算他在训练集和验证集上的误差的均值和方差.

对于任意一个模型, 我们都可以使用下面的方式来进行K-Fold的训练.

  1. # 对于一个固定的模型, 使用K-Fold来计算他的误差
  2. def k_fold(train_features, train_labels, num_epochs, learning_rate, weight_decay, batch_size):
  3.     train_l_sum, valid_l_sum = [], []
  4.     rkf = model_selection.RepeatedKFold(n_splits=5, n_repeats=5, random_state=777) # 这里返回的是index
  5.     for train_index, valid_index in rkf.split(train_features):
  6.         data = (train_features[train_index], train_labels[train_index], train_features[valid_index], train_labels[valid_index])
  7.         net = get_net()
  8.         train_ls, valid_ls = train(net, *data, num_epochs, learning_rate, weight_decay, batch_size)
  9.         train_l_sum.append(train_ls[-1])
  10.         valid_l_sum.append(valid_ls[-1])
  11.         print(f'train rmse {float(train_ls[-1]):f}, '
  12.               f'valid rmse {float(valid_ls[-1]):f}')
  13.     return train_l_sum, valid_l_sum

于是, 我们就可以使用下面的方式来验证我们的模型.

  1. num_epochs, lr, weight_decay, batch_size = 100, 5, 0, 64
  2. train_l, valid_l = k_fold(train_features, train_labels, num_epochs, lr, weight_decay, batch_size)
  3. print('avg train rmse: {}, var train rmse: {}, avg valid rmse: {}, var valid rmse: {}'.format(np.mean(train_l), np.var(train_l), np.mean(valid_l), np.var(valid_l)))
  4. """
  5. train rmse 0.169092, valid rmse 0.150075
  6. train rmse 0.160831, valid rmse 0.190446
  7. train rmse 0.161771, valid rmse 0.185632
  8. train rmse 0.172952, valid rmse 0.158034
  9. train rmse 0.163542, valid rmse 0.170307
  10. train rmse 0.163597, valid rmse 0.170964
  11. train rmse 0.166117, valid rmse 0.174052
  12. train rmse 0.167874, valid rmse 0.170353
  13. train rmse 0.168679, valid rmse 0.175075
  14. train rmse 0.161861, valid rmse 0.171495
  15. train rmse 0.167337, valid rmse 0.154704
  16. train rmse 0.162929, valid rmse 0.176299
  17. train rmse 0.166023, valid rmse 0.163900
  18. train rmse 0.162515, valid rmse 0.189767
  19. train rmse 0.169079, valid rmse 0.165148
  20. train rmse 0.170753, valid rmse 0.166659
  21. train rmse 0.163065, valid rmse 0.160626
  22. train rmse 0.168117, valid rmse 0.182729
  23. train rmse 0.165373, valid rmse 0.183683
  24. train rmse 0.163760, valid rmse 0.171788
  25. train rmse 0.163138, valid rmse 0.167196
  26. train rmse 0.169106, valid rmse 0.192142
  27. train rmse 0.163955, valid rmse 0.168445
  28. train rmse 0.168268, valid rmse 0.168536
  29. train rmse 0.167822, valid rmse 0.159234
  30. avg train rmse: 0.16590223610401153, var train rmse: 9.853495928808797e-06, 
  31. avg valid rmse: 0.17149150609970093, var valid rmse: 0.00011951098341428476
  32. """

最后, 我们只需要对不同的模型都进行上面同样的操作, 选出一个误差比较小, 同时方差也是比较小的模型即可.

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2020年9月5日07:56:19
  • 转载请务必保留本文链接：https://mathpretty.com/12711.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: