交叉检验(Cross Validation)简介

王 茂南
王 茂南
王 茂南
3091
文章
75
评论
2019年4月17日07:46:21
评论 4023字阅读13分24秒
摘要这一篇简单介绍一下交叉检验的技术，以及给出一个交叉检验的实例。交叉检验可以进行模型的选择，查看模型是否存在过拟合或是欠拟合的状态。

交叉检验技术简介

交叉检验原因

我们认为使用模型在做一次检查存在随机性，所以我们希望进行多次实验，来获得同一个model在不同数据集上的err的均值和方差（看一下是不是err的均值一直很大，说明模型不能很好的表达你的问题。如果err的方差很大，说明模型每次在不同数据集上训练的结果相差很大，很可能模型过于复杂，存在过拟合的可能），从而来判断模型的好坏，来选择一个好的模型。于是，就有了交叉检验的方法。（我的简单的理解）

具体步骤

  1. 将training set 分为N分, 其中1/N作为测试集;
  2. 使用不同的model(不同的参数)进行N此训练, 并在测试集上测试, 计算误差;
  3. 根据误差的均值与标准差, 选择出最好的模型;
  4. 将找出的model在整个training set上进行训练;

在下图中可以看到，我们将training set分成三份，每次两份作为训练集。将三个model分别进行训练和测试，这样会进行9次训练，接着计算三个model误差的均值与方差，选出最好的一个模型。

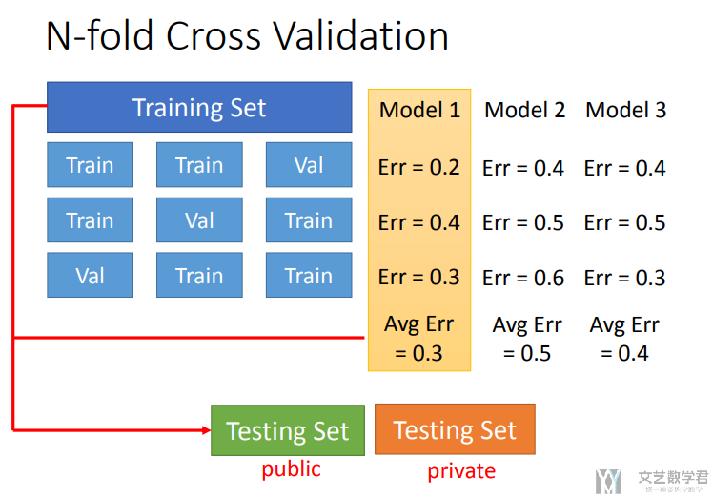
交叉检验(Cross Validation)简介

交叉检验实验

RepeatedKFold的使用

关于CV的实验，接下来会使用sklearn中的RepeatedKFold进行完成。下面先简单看一下如何进行使用。

  1. X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
  2. y = np.array([0, 0, 1, 1])
  3. rkf = model_selection.RepeatedKFold(n_splits=2, n_repeats=1, random_state=777)
  4. for train_index, test_index in rkf.split(X):
  5.     print("train_index:{};\ntest_index:{}".format(train_index,test_index))
  6.     X_train, X_test = X[train_index], X[test_index]
  7.     y_train, y_test = y[train_index], y[test_index]
  8.     print("X_train:\n{}\n---\n".format(X_train))

他会输出list的index，在使用的时候，只需要使用X[index]这种形式即可。我们看一下最终的输出结果。

交叉检验(Cross Validation)简介

生成数据集

我们还是自己生成一些模拟的数据集，为了方便后面的测试；

  1. # 生成随机数据
  2. np.random.seed(7)
  3. x = np.linspace(1, 30, 30)
  4. y = 2*x + 0.7*x**2 - 20*np.sin(x) - 20*np.cos(x) + 5*np.random.rand(30)
  5. plt.style.use("ggplot") # 使用美观的样式
  6. plt.scatter(x, y)
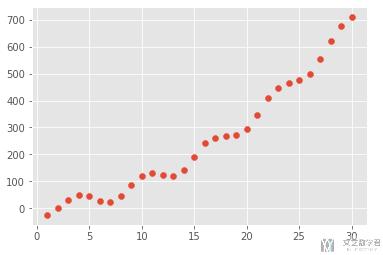
交叉检验(Cross Validation)简介

模型的选择

我们想通过CV(交叉检验)的方式选择出最好的参数，在这里我们希望选择出最好的惩罚系数的大小。

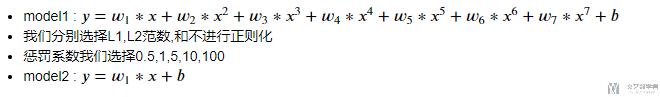
交叉检验(Cross Validation)简介

生成测试模型

  1. alpha_list = [0.5,1,5,10,100]
  2. model_list_Lasso = [Lasso(alpha=i,normalize=True) for i in alpha_list]
  3. model_list_Ridge = [Ridge(alpha=i,normalize=True) for i in alpha_list]

模型的测试与选择

我们以LASSO模型为例，详细代码查看文末链接地址。我们每次根据不同的数据集进行训练，同时计算每个模型的误差的均值与标准差。

  1. err_list_Lasso = [] # Lasso回归的误差
  2. Polynomia_7 = PolynomialFeatures(degree=7)
  3. rkf = model_selection.RepeatedKFold(n_splits=5, n_repeats=50, random_state=777) # 这里返回的是index
  4. for model in model_list_Lasso:
  5.     # 每次选出一个模型
  6.     err_list = []
  7.     for train_index, test_index in rkf.split(x):
  8.         # 计算每次的误差
  9.         # 模型的拟合
  10.         x_polynomia7 = Polynomia_7.fit_transform(x[train_index].reshape(-1,1)) # 数据的转换(训练集)
  11.         model.fit(x_polynomia7,y[train_index]) # 计算模型参数
  12.         # 模型的测试
  13.         x_test_polynomia7 = Polynomia_7.fit_transform(x[test_index].reshape(-1,1)) # 数据的转换(测试集)
  14.         model_pre = model.predict(x_test_polynomia7) # 在测试集上预测
  15.         err = mean_squared_error(model_pre,y[test_index]) # 计算误差
  16.         err_list.append(err)
  17.     err_list_Lasso.append(err_list)

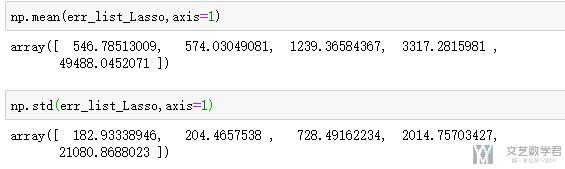
模型的均值与方差如下所示：

交叉检验(Cross Validation)简介

我们依次可以对剩下的模型进行同样的操作，之后可以绘制出如下的箱线图。

模型的选择

上面的所有误差可以绘制出的箱线图如下所示：

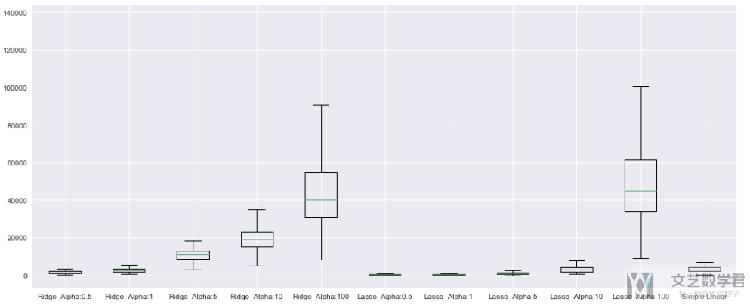
交叉检验(Cross Validation)简介

由于当惩罚系数是100时，方差太大，最后绘制出的图像不好看，我们把惩罚系数是100去掉再看一下。

  1. plt.style.use('seaborn')
  2. fig = plt.figure(figsize=(17,7))
  3. ax = fig.add_subplot(1, 1, 1)
  5. err_lists = err_list_Ridge+err_list_Lasso+[err_list_simple]
  6. pic_labels = ["Ridge_Alpha:{}".format(i) for i in alpha_list] + ["Lasso_Alpha:{}".format(i) for i in alpha_list] + ['Simple Linear']
  7. ax.boxplot(err_lists, labels=pic_labels)
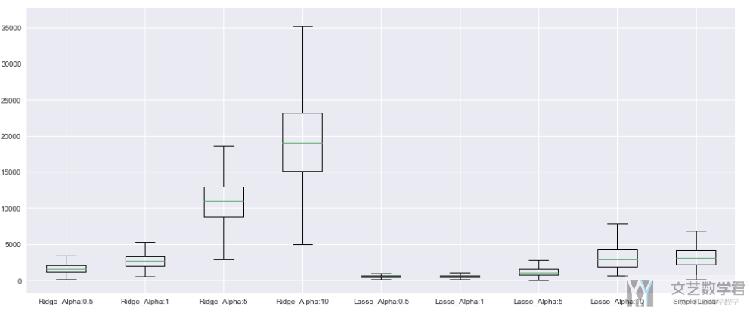
交叉检验(Cross Validation)简介

可以看到惩罚系数选择较小的时候模型效果还是不错的，总体的误差不大，且浮动也不大。下面我们将选择出最好的模型绘制出来。

结果的绘制

我们绘制一些延拓的效果。

  1. # ---------
  2. # 模型的定义
  3. # ---------
  4. model_lasso = Lasso(alpha=0.5,normalize=True)
  5. model_Ridge = Ridge(alpha=0.5,normalize=True)
  6. model_linear = LinearRegression()
  8. # ----------------------------------
  9. # 模型的训练, 使用整个训练集进行训练
  10. # ----------------------------------
  11. x_polynomia7 = Polynomia_7.fit_transform(x.reshape(-1,1))
  12. model_lasso.fit(x_polynomia7,y)
  13. model_Ridge.fit(x_polynomia7,y)
  14. model_linear.fit(x.reshape(-1,1),y)
  16. # ---------
  17. # 预测的数据集
  18. # ---------
  19. x_test = np.linspace(1, 42, 42)
  20. y_test = 2*x_test + 0.7*x_test**2 - 20*np.sin(x_test) - 20*np.cos(x_test) + 5*np.random.rand(42)
  22. x_test_polynomia7 = Polynomia_7.fit_transform(x_test.reshape(-1,1))
  24. # ----
  25. # 绘图
  26. # ----
  27. plt.style.use('seaborn')
  28. fig = plt.figure(figsize=(13,7))
  29. ax = fig.add_subplot(1, 1, 1)
  31. model1_pre = model_lasso.predict(x_test_polynomia7)
  32. model2_pre = model_Ridge.predict(x_test_polynomia7)
  33. model3_pre = model_linear.predict(x_test.reshape(-1,1))
  35. plt.scatter(x_test,y_test,c='red',label='real') # 画出原图
  36. plt.plot(x_test,model1_pre,c='green',label='Lasso') # 未使用正则化
  37. plt.plot(x_test,model2_pre,c='blue',label='Ridge') # l1范数
  38. plt.plot(x_test,model3_pre,c='darkviolet',label='None') # l2范数
  39. plt.legend()
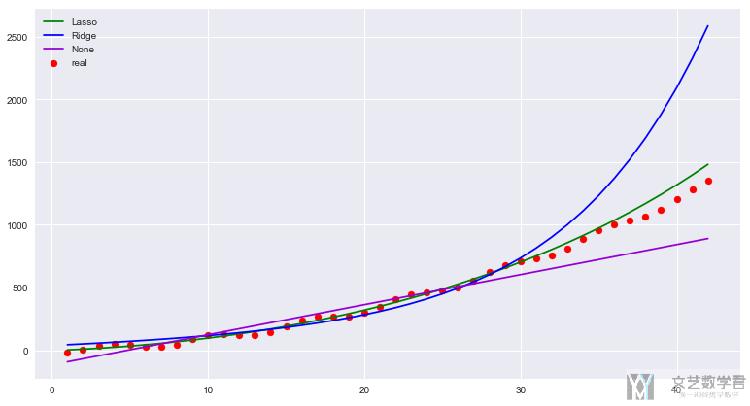
交叉检验(Cross Validation)简介

其实总体上来看，LASSO的效果还是可以的。看一下模型最后的系数，可以看到LASSO回归比Ridge回归少一个高次项的系数，所以向后延拓的时候不会高太快。（之前在数据生成的时候只用到了最高是2次）

交叉检验(Cross Validation)简介

项目链接

https://github.com/wmn7/ML_Practice/tree/master/2019_04_14

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2019年4月17日07:46:21
  • 转载请务必保留本文链接：https://mathpretty.com/10283.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: