文章目录(Table of Contents)
简介
这一部分会记录一些基础的矩阵运算的知识, 一些基础的优化算法的知识. 包括拉格朗日乘子法, 矩阵的基础运算, 矩阵的SVD分解等.
这一部分还有待完善,先把一些照片贴在这里,方便寻找。
求高斯分布均值方差
之前写过一个比较完整的, 就直接看下面的参考链接即可. 这里有详细的推导高斯分布均值和方差的过程.
参考链接: 求高斯分布的均值和方差
求解最优化问题
拉格朗日乘子法例题--等式约束
我们要注意, 使用拉格朗日乘子法是将有约束的问题转换为没有约束的问题(这里的限制是等式限制), 所以下面列的式子就不用考虑约束的问题了.
一个约束条件

多个约束条件
当原始的式子有多个约束条件的时候, 我们也是使用类似的方法进行求解, 我们下面来看一个例子(可以直接Google搜索关键词: Lagrange multiplier example with two constraints, 参考连接: An Example With Two Lagrange Multipliers).
我们要解决下面的最优化问题, 下面是有两个约束条件.

于是我们可以列出如下的目标函数.
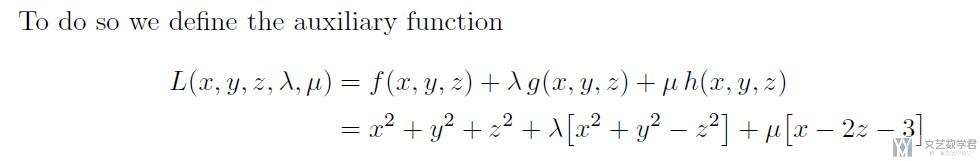
要解这个目标函数, 我们对其求偏导数(要求5个偏导数), 偏导数结果如下所示, 最后我们需要进行分类讨论.
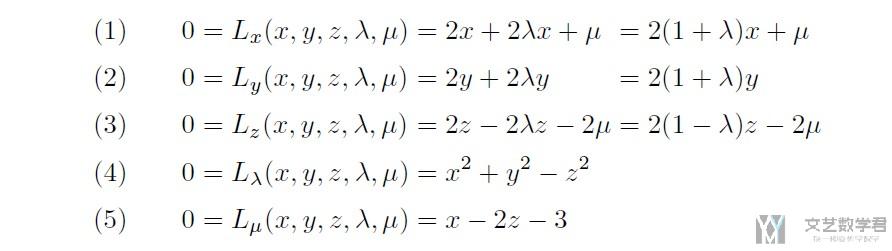
后面的求解过程就不细说了, 可以参考上面的参考链接.
矩阵运算
这里的内容大部分来源于下面这本书. The Matrix Cookbook
有很多关于矩阵的运算都可以在上面进行查询.
矩阵、向量和标量形式的导数
一阶导数(这个是比较常用的)--书本的Page10.
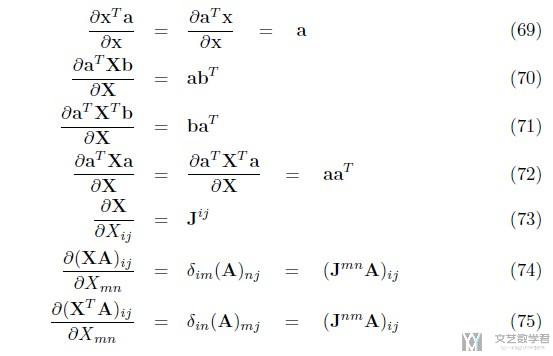
矩阵SVD分解
这里我们举一个SVD分解的例子, 对于2*2的矩阵((1,2),(1,2))进行分解.
- a = {{1, 2}, {1, 2}};
- {u, w, v} = SingularValueDecomposition[a]

我们将这三个相乘, 可以还原uwTranspose(v) = a.
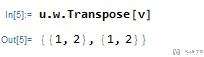
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-












评论