简单GAN的实验–生成高斯分布数据(Pytorch)

王 茂南
王 茂南
王 茂南
3081
文章
75
评论
2019年7月21日07:17:32
评论1 7729字阅读25分45秒
摘要这一篇文章主要介绍关于GAN的实验, 使用GAN来生成服从高斯分布的数据, 给出简单的步骤和最终的结果分析.

简介

这一篇做一下GAN的简单实验，主要参考资料如下: Generative Adversarial Networks (GANs) in 50 lines of code (PyTorch)，这是GAN的第一个实验.

这一篇我们会使用GAN来生成服从高斯分布的数据，我会稍微对上面的代码进行修改.

完整的代码链接: GAN实验代码链接

实验的简单步骤

首先我们介绍一下这个实验的简单步骤。

  • 我们的training dataset是服从mean=4, std=1.25的高斯分布, 这是用来训练D的真实的数据.
  • 我们取50维的均匀分布, 用作G的输入, 用来生成虚假的高斯分布的数据.
  • 最后, 我们会训练分类器D和生成器G.

实验过程

实验准备

我们首先做一下实验的准备工作, 首先导入库.

  1. import numpy as np
  2. from matplotlib import pyplot as plt
  4. import torch
  5. import torch.nn as nn
  6. import torch.optim as optim
  7. from torch.autograd import Variable
  8. from torch.optim import lr_scheduler

接着我们定义一个处理数据的函数, 这个函数输入时一组数据, 输出是这组数据的均值, 方差, 偏度和峰度, 我们用这四个数据来判断这组数据是否是服从高斯分布的数据.

  1. def get_moments(ds):
  2.     """
  3.     - Return the first 4 moments of the data provided
  4.     - 返回一个数据的四个指标, 分别是均值, 方差, 偏度, 峰读
  5.     - 我们希望通过这四个指标, 来判断我们生成的数据是否是需要的数据
  6.     """
  7.     finals = []
  8.     for d in ds:
  9.         mean = torch.mean(d) # d的均值
  10.         diffs = d - mean
  11.         var = torch.mean(torch.pow(diffs, 2.0))
  12.         std = torch.pow(var, 0.5) # d的方差
  13.         zscores = diffs / (std+0.001) # 对原始数据 zscores = (d-mean)/std
  14.         skews = torch.mean(torch.pow(zscores, 3.0)) # 峰度
  15.         kurtoses = torch.mean(torch.pow(zscores, 4.0)) - 3.0  # excess kurtosis, should be 0 for Gaussian
  16.         final = torch.cat((mean.reshape(1,), std.reshape(1,), skews.reshape(1,), kurtoses.reshape(1,)))
  17.         # 这里返回的是高斯分布的四个特征
  18.         finals.append(final)
  19.     return torch.stack(finals)

 训练样本的准备

首先是用来生成服从高斯分布的样本, 即training set中的数据. 这个数据是生成真实的数据, 被用于模仿。

  1. def get_distribution_sampler(mu, sigma, batchSize, FeatureNum):
  2.     """
  3.     Generate Target Data, Gaussian
  4.     Input
  5.     - mu: 均值
  6.     - sugma: 方差
  7.     Output
  8.     """
  9.     return Variable(torch.Tensor(np.random.normal(mu, sigma, (batchSize, FeatureNum))))

我们生成500个数据样本进行绘图测试，代码如下

  1. data_mean = 4
  2. data_stddev = 1.25
  3. batch_size = 1
  4. featureNum = 500
  6. d_real_data = get_distribution_sampler(data_mean, data_stddev, batch_size, featureNum)

最终的分布如下图所示.

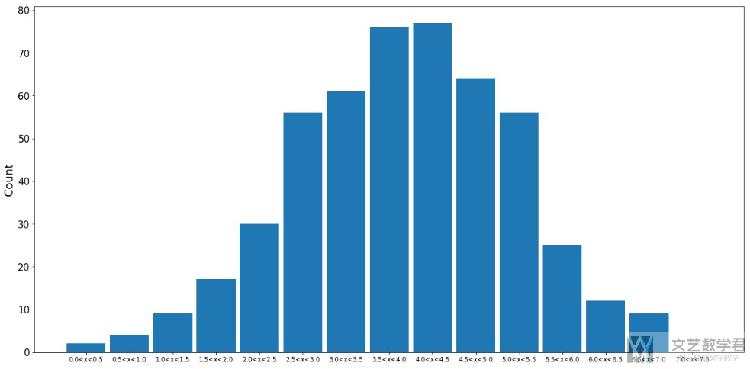
简单GAN的实验–生成高斯分布数据(Pytorch)

这是输入生成器G中的数据, 用来生成服从均匀分布的数据.

  1. def get_generator_input_sampler(m, n):
  2.     """
  3.     Uniform-dist data into generator, _NOT_ Gaussian
  4.     Input
  5.     - m: 表示batchsize
  6.     - n: 表示feature count
  7.     Output
  8.     - 返回的是生成数据的分布
  9.     """
  10.     return torch.rand(m, n)

定义分类器和生成器

下面我们定义生成器和分类器。首先是定义生成器，下面是简单的介绍.

  • generator是一个普通的前向传播网络
  • generator使用的是tanh激活函数
  • generator输入是均值分布(来自I的数据)
  • generator的任务是输出模仿真实的高斯分布的数据
  1. class Generator(nn.Module):
  2.     def __init__(self, input_size, hidden_size, output_size, f):
  3.         super(Generator, self).__init__()
  4.         self.map1 = nn.Linear(input_size, hidden_size)
  5.         self.map2 = nn.Linear(hidden_size, hidden_size)
  6.         self.map3 = nn.Linear(hidden_size, output_size)
  7.         self.relu = nn.ReLU()
  8.         self.f = f # 激活函数
  10.     def forward(self, x):
  11.         x = self.map1(x)
  12.         x = self.relu(x)
  13.         x = self.map2(x)
  14.         x = self.relu(x)
  15.         x = self.map3(x)
  16.         return x

接着定义分类器, 下面是对分类器的简单介绍

  • discriminator和generator一样, 也是简单的前向传播网络
  • discriminator使用的是sigmoid函数
  • discriminator使用真实数据和G产生的数据
  • 最后的label是0与1, 从真实的高斯分布中的数据label是1, 从G中产生的数据label是0
  1. class Discriminator(nn.Module):
  2.     def __init__(self, input_size, hidden_size, output_size, f):
  3.         super(Discriminator, self).__init__()
  4.         self.map1 = nn.Linear(input_size, hidden_size)
  5.         self.map2 = nn.Linear(hidden_size, hidden_size)
  6.         self.map3 = nn.Linear(hidden_size, output_size)
  7.         self.relu = nn.ReLU()
  8.         self.f = f
  10.     def forward(self, x):
  11.         x = self.relu(self.map1(x))
  12.         x = self.relu(self.map2(x))
  13.         x = self.f(self.map3(x))# 最后生成的是概率
  14.         return x

模型开始训练

首先说明一下训练的简单步骤:

  • 首先训练D, 我们使用real data vs. fake data, with accurate labels
  • 接着我们训练G来使得其生成的数据无法被D正确分辨(这时候fix住D的参数, 使得G产生数据, 使得D预测的label是1)
  • 接着重复上面的两个操作

对于代码的简单说明(这个很重要)

  • 对于分类器来说, 输入维度是4, 表示一组数据的均值, 方差, 偏度和峰度, 输出是一维, 表示判断是真实数据或不是真实数据
  • 对于生成器来说, 输入维度是50, 表示我们每次随机输入一个50维的均匀分布的数据, 输出是500, 表示我们希望产生500个数, 这500个数服从mean=4, std=1.25的高斯分布。
  1. d_input_size = 4
  2. d_hidden_size = 10
  3. d_output_size = 1
  4. discriminator_activation_function = torch.sigmoid
  6. g_input_size = 50
  7. g_output_size = 200
  8. g_output_size = 500
  9. generator_activation_function = torch.tanh
  11. featureNum = g_output_size # 一组样本有500个服从正太分布的数据
  12. minibatch_size = 10 # batch_size的大小
  14. num_epochs = 2001
  15. d_steps = 20 # discriminator的训练轮数
  16. g_steps = 20 # generator的训练轮数
  18. # ----------
  19. # 初始化网络
  20. # ----------
  21. D = Discriminator(input_size=d_input_size,
  22.                   hidden_size=d_hidden_size,
  23.                   output_size=d_output_size,
  24.                   f=discriminator_activation_function)
  27. G = Generator(input_size=g_input_size,
  28.               hidden_size=g_hidden_size,
  29.               output_size=g_output_size,
  30.               f=generator_activation_function)
  32. # ----------------------
  33. # 初始化优化器和损失函数
  34. # ----------------------
  35. d_learning_rate = 0.0001
  36. g_learning_rate = 0.0001
  39. criterion = nn.BCELoss()  # Binary cross entropy: http://pytorch.org/docs/nn.html#bceloss
  40. d_optimizer = optim.Adam(D.parameters(), lr=d_learning_rate)
  41. g_optimizer = optim.Adam(G.parameters(), lr=g_learning_rate)
  43. d_exp_lr_scheduler = optim.lr_scheduler.CosineAnnealingLR(d_optimizer, T_max = d_steps*5, eta_min=0.00001)
  44. g_exp_lr_scheduler = optim.lr_scheduler.CosineAnnealingLR(g_optimizer, T_max = g_steps*5, eta_min=0.00001)
  47. G_mean = [] # 生成器生成的数据的均值
  48. G_std = [] # 生成器生成的数据的方差
  50. for epoch in range(num_epochs):
  51.     # -------------------
  52.     # Train the Detective
  53.     # -------------------
  54.     for d_index in range(d_steps):
  55.         # Train D on real+fake
  56.         d_exp_lr_scheduler.step()
  57.         D.zero_grad()
  59.         # Train D on real, 这里的label是1
  60.         d_real_data = get_distribution_sampler(data_mean, data_stddev, minibatch_size, featureNum) # 真实的样本
  61.         d_real_decision = D(get_moments(d_real_data)) # 求出数据的四个重要特征
  62.         d_real_error = criterion(d_real_decision, Variable(torch.ones([minibatch_size, 1]))) # 计算error
  63.         d_real_error.backward() # 进行反向传播
  65.         # Train D on fake, 这里的label是0
  66.         d_gen_input = get_generator_input_sampler(minibatch_size, g_input_size)
  67.         d_fake_data = G(d_gen_input)
  68.         d_fake_decision = D(get_moments(d_fake_data))
  69.         d_fake_error = criterion(d_fake_decision, Variable(torch.zeros([minibatch_size, 1])))
  70.         d_fake_error.backward()
  72.         # Optimizer
  73.         d_optimizer.step()
  75.     # -------------------
  76.     # Train the Generator
  77.     # -------------------
  78.     for g_index in range(g_steps):
  79.         # Train G on D's response(使得G生成的x让D判断为1)
  80.         g_exp_lr_scheduler.step()
  81.         G.zero_grad()
  83.         gen_input = get_generator_input_sampler(minibatch_size, g_input_size)
  84.         g_fake_data = G(gen_input) # 使得generator生成样本
  85.         dg_fake_decision = D(get_moments(g_fake_data)) # D来做的判断
  86.         g_error = criterion(dg_fake_decision, Variable(torch.ones([minibatch_size, 1])))
  88.         G_mean.append(g_fake_data.mean().item())
  89.         G_std.append(g_fake_data.std().item())
  91.         g_error.backward()
  92.         g_optimizer.step()
  94.     if epoch%10==0:
  95.         print("Epoch: {}, G data's Mean: {}, G data's Std: {}".format(epoch, G_mean[-1], G_std[-1]))
  96.         print("Epoch: {}, Real data's Mean: {}, Real data's Std: {}".format(epoch, d_real_data.mean().item(), d_real_data.std().item()))
  97.         print('-'*10)

我们就使用上面的代码进行训练。

结果分析

我们绘制出生成器产生的服从正太分布的数据.

  1. # ----------------------
  2. # 计算每个范围的数据个数
  3. # ----------------------
  4. binRange = np.arange(0,8,0.5)
  5. hist1,_ = np.histogram(g_fake_data.squeeze().detach().numpy(), bins=binRange)
  7. # --------
  8. # 绘制图像
  9. # --------
  10. fig, ax1 = plt.subplots()
  11. fig.set_size_inches(20, 10)
  12. plt.set_cmap('RdBu')
  13. x = np.arange(len(binRange)-1)
  14. w=0.3
  15. # 绘制多个bar在同一个图中, 这里需要控制width
  16. plt.bar(x, hist1, width=w*3, align='center')
  17. # 设置坐标轴的标签
  18. ax1.yaxis.set_tick_params(labelsize=15) # 设置y轴的字体的大小
  19. ax1.set_xticks(x) # 设置xticks出现的位置
  21. # 创建xticks
  22. xticksName = []
  23. for i in range(len(binRange)-1):
  24.     xticksName = xticksName + ['{}<x<{}'.format(str(np.round(binRange[i],1)), str(np.round(binRange[i+1],1)))]
  25. ax1.set_xticklabels(xticksName)
  27. # 设置坐标轴名称
  28. ax1.set_ylabel("Count", fontsize='xx-large')
  29. plt.show()

最终的实验结果如下图所示，可以看到基本上还是挺像的。

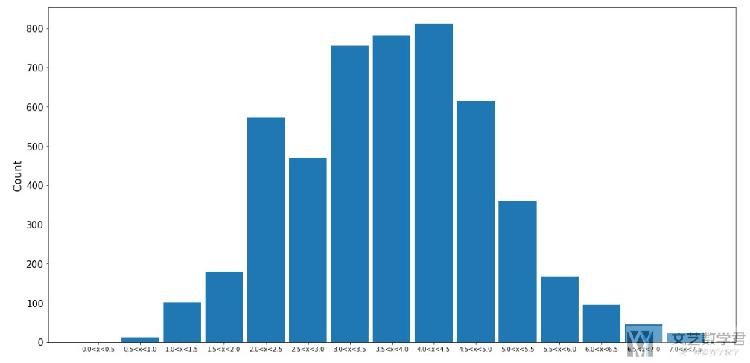
简单GAN的实验–生成高斯分布数据(Pytorch)

我们绘制出均值和方差的变化情况。均值的变化如下, 可以看到最后会在4左右徘徊，是符合正确数据的均值的。

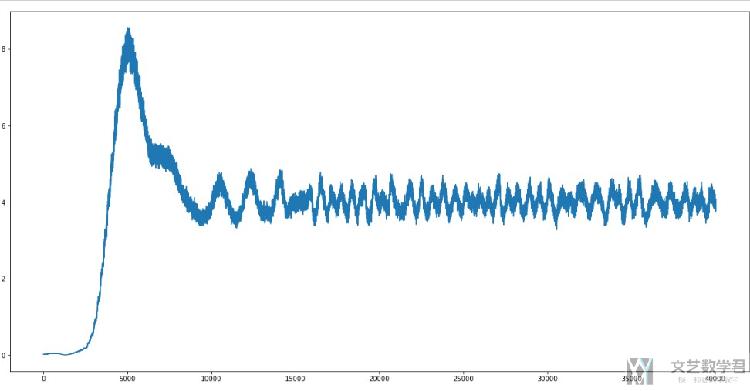
简单GAN的实验–生成高斯分布数据(Pytorch)

同样，方差最后也是会趋于1.25，如下图所示。

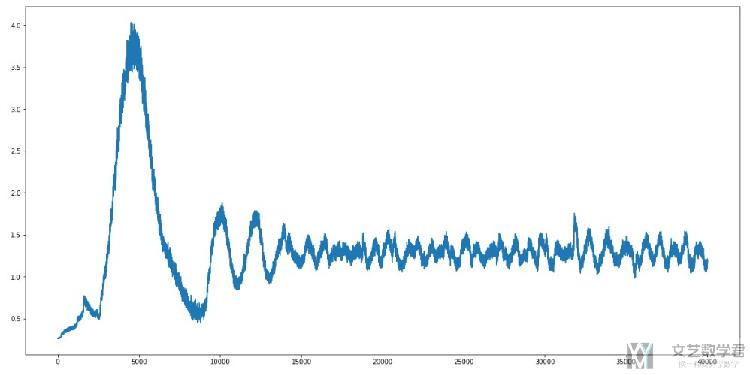
简单GAN的实验–生成高斯分布数据(Pytorch)

所以，总体来说，生成器生成的结果还是不错的.

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2019年7月21日07:17:32
  • 转载请务必保留本文链接：https://mathpretty.com/10808.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: