文章目录(Table of Contents)
前言
这一篇会使用TensorFlow,Keras和PyTorch三种框架实现线性回归,也是作为简单了解一下这三种最常用的深度学习框架的使用。做这个线性回归,既可以顺一遍整个框架的流程,也不会太麻烦。
这三个框架,我个人使用起来觉得Keras是会方便一些(Keras底层是TensorFlow),只不过又做了一次封装。PyTorch使用起来也不是很麻烦。怎么说呢,多用几次,多看看文档,多了解一下框架设计的时候的想法。
之后的话会实现一些经典的神经网络。
三种框架实现线性回归
首先我们先准备一下数据集:
数据准备
我们首先准备好需要回归的数据,并用图形显示出来:
- import numpy as np
- from matplotlib import pyplot as plt
- %matplotlib inline
- np.random.seed(7)
- x = np.linspace(1, 10, 50)
- y = 2 * x + 3 * np.random.rand(50)
- plt.style.use("ggplot") # 使用美观的样式
- plt.scatter(x, y)
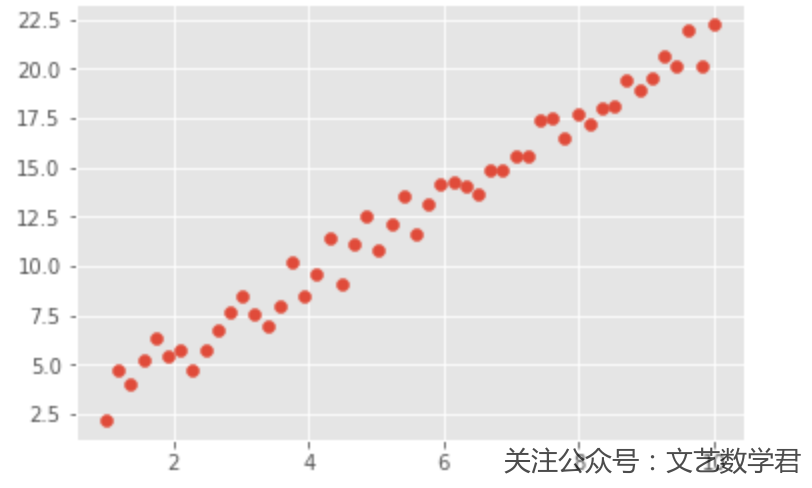
下面我们依次按照TensorFlow,Keras和PyTorch这三个框架的顺序进行回归。
TensorFlow
- TensorFlow文档
- https://www.tensorflow.org/api_docs/python/
- import tensorflow as tf
- import os
- # --------
- # 初始化变量
- # --------
- X = x.reshape(-1,1)
- Y = y.reshape(-1,1)
- # 定义占位量,之后为了分批训练
- x_batch = tf.placeholder(tf.float32, [None, 1])
- y_batch = tf.placeholder(tf.float32, [None, 1])
- # 需要预测的数据
- X_pre = np.linspace(0, 11, 1000).reshape(-1,1)
- # ---------
- # 定义网络层
- # ---------
- dense_1 = tf.layers.dense(inputs=x_batch, units=1, activation=None)
- # ---------
- # 定义损失函数和优化器
- # ---------
- loss = tf.losses.mean_squared_error(labels=dense_1,predictions=y_batch)
- # 优化器
- learning_rate = 0.01
- optimizer = tf.train.GradientDescentOptimizer(learning_rate = learning_rate)
- training_op = optimizer.minimize(loss)
- # -------
- # 训练模型
- # -------
- batch_size = 25 # 定义batch_size
- init = tf.global_variables_initializer() # 之后可以对所有节点初始化
- n_epochs = 10
- loss_list = [] # 存储训练的误差
- with tf.Session() as sess:
- sess.run(init)
- for epochs in range(n_epochs):
- train_batch = zip(range(0, len(x), batch_size), range(batch_size, len(x) + 1, batch_size))
- i = 0
- for start, end in train_batch:
- X_batch = X[start:end] # 获得X的小批量训练数据
- Y_batch = Y[start:end] # 获得Y的小批量训练数据
- loss_epoch = sess.run(loss, feed_dict={x_batch: X_batch, y_batch: Y_batch}) # 计算误差
- print("Epoch", epochs, 'i', i, "loss =", loss_epoch)
- loss_list.append(loss_epoch)
- sess.run(training_op, feed_dict={x_batch: X_batch, y_batch: Y_batch}) # 进行反向传播
- i = i + 1
- result = sess.run(dense_1, feed_dict={x_batch : X_pre})
- # ----------
- # 绘制预测图像
- # ----------
- plt.style.use("ggplot") # 使用美观的样式
- plt.scatter(x, y)
- plt.scatter(X_pre,result)
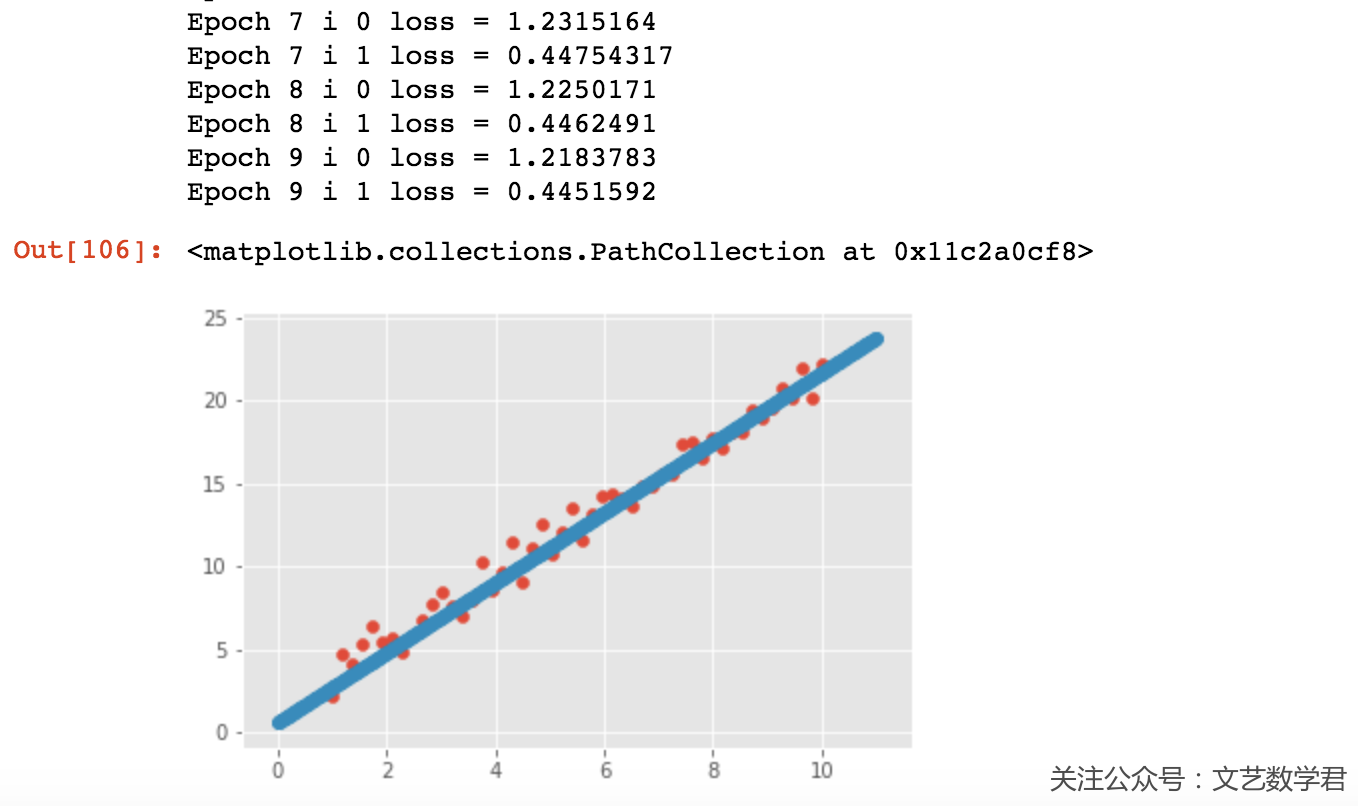
上面就是使用TensorFlow进行回归的整个流程,虽然只有50个数据,但是作为样例还是使用了batch进行训练。
我们看一下部分输出,训练10次,每次传入25个数据进行训练,从图像上看直线拟合效果还是很好的:
Keras
- from keras.models import Sequential
- from keras.layers import Dense
- # --------
- # 初始化数据
- # --------
- X = x # 就是numpy的类型
- Y = y
- # ------
- # 模型构建
- # ------
- model = Sequential() # 声明序贯模型
- # 这里input_dim为输入向量的维度,units为输出的维度
- model.add(Dense(input_dim=1, units=1))
- # -------
- # 定义模型的损失函数与优化器
- # -------
- model.compile(loss='mean_squared_error', optimizer='sgd')
- # -------
- # 模型训练
- # -------
- model.fit(X, Y, epochs=10, batch_size=32)
- # ----------
- # 画出拟合图像
- # ----------
- weight = model.get_weights()[0] # 权重
- bias = model.get_weights()[1] # 偏置项
- plt.style.use("ggplot") # 使用美观的样式
- plt.scatter(x, y)
- x_plot = np.linspace(1, 10, 500)
- print('weight : ', weight, 'bias : ', bias)
- plt.plot(x_plot, (weight*x_plot+bias).flatten(), c='black') # 这里要转为numpy才能绘制
可以看到Keras的代码会比上面使用TensorFlow少一些,同时使用Keras来设置批训练等是很方便的。我们这里训练了10次,可以看一下最后部分输出的结果和拟合的图像:
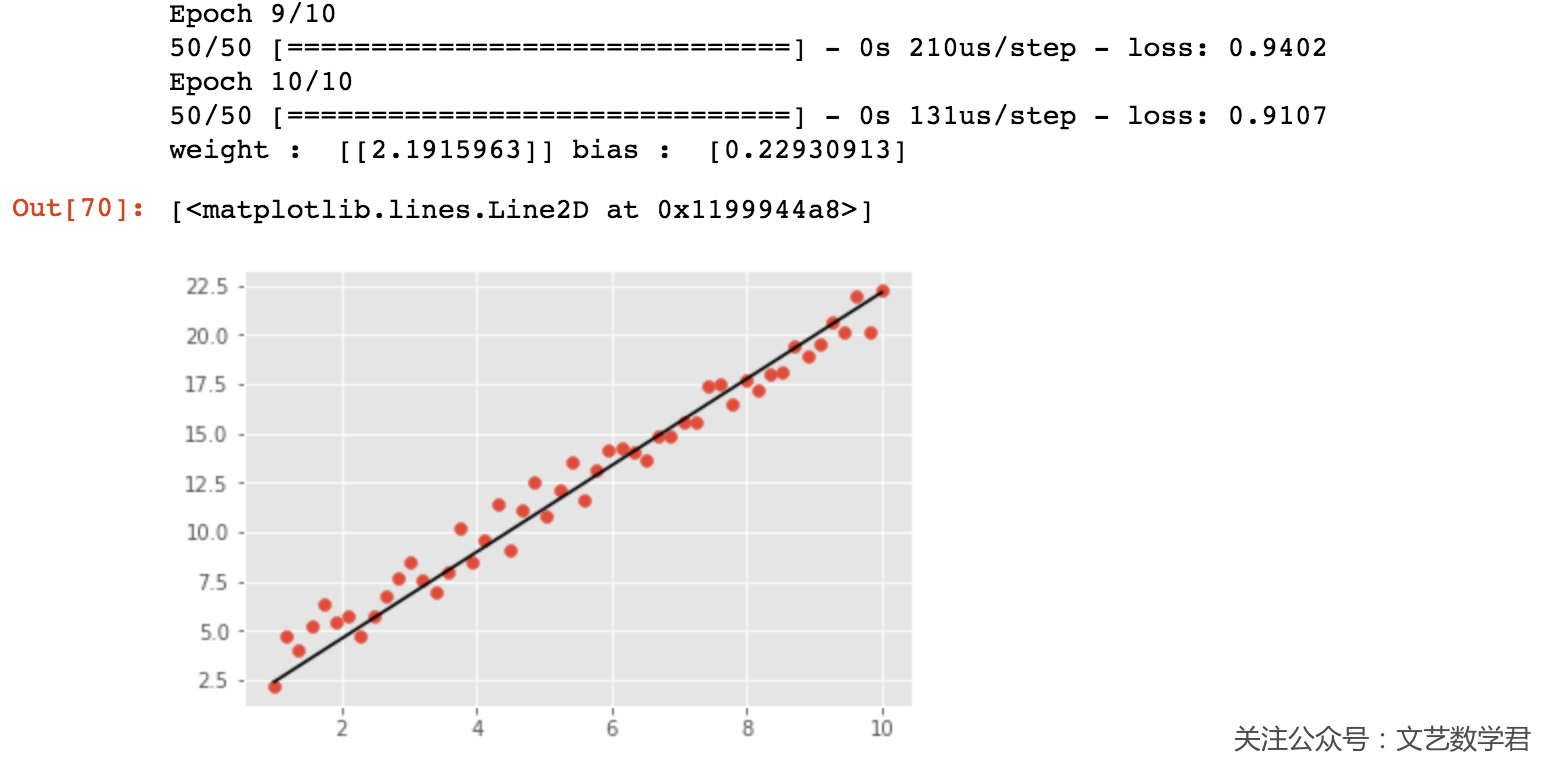
同样可以看到直线的拟合效果还是很不错的。
PyTorch
- PyTorch文档
- https://pytorch.org/docs/stable/index.html
- import torch as t
- import torch.nn as nn
- from torch.nn.functional import sigmoid
- from torch import optim
- from torch.autograd import Variable
- import torch.utils.data as Data
- # -------
- # 定义网络
- # -------
- class LinearRegressionModel(nn.Module):
- def __init__(self):
- super(LinearRegressionModel, self).__init__() # 等价于 nn.Module.__init__(self)
- self.linear1 = nn.Linear(1, 1)
- def forward(self, x):
- out = self.linear1(x)
- return out
- # ------
- # 定义损失函数和优化器
- # ------
- model = LinearRegressionModel() # 实例化模型
- loss_fn = nn.MSELoss(size_average=True) # 定义损失函数,这里True表示会求平均
- optimiser = optim.SGD(params=model.parameters(), lr=0.01) # 定义优化器
- # ------
- # 定义变量
- # ------
- X = t.Tensor(x).reshape(-1,1) # 输入 x 张量
- # X = Variable(x.reshape(len(x),1)) # 也可以通过这种方式进行shape的转换
- Y = t.Tensor(y).reshape(-1,1) # 输入 y 张量
- # 使用batch训练
- torch_dataset = Data.TensorDataset(X, Y) # 合并训练数据和目标数据
- MINIBATCH_SIZE = 25
- loader = Data.DataLoader(
- dataset=torch_dataset,
- batch_size=MINIBATCH_SIZE,
- shuffle=True,
- num_workers=2 # set multi-work num read data
- )
- # ------
- # 进行训练
- # ------
- for epoch in range(100):
- for step, (batch_x, batch_y) in enumerate(loader):
- optimiser.zero_grad() # 梯度清零
- out = model(batch_x) # 前向传播
- loss = loss_fn(out, batch_y) # 计算损失
- loss.backward() # 反向传播
- optimiser.step() # 随机梯度下降
- if epoch % 10 == 0:
- print('epoch {}, step {}, loss {}'.format(epoch, step, loss.item()))
- # ----------
- # 画出拟合图像
- # ----------
- weight = model.state_dict()['linear1.weight'] # 权重
- bias = model.state_dict()['linear1.bias'] # 偏置项
- plt.style.use("ggplot") # 使用美观的样式
- plt.scatter(x, y)
- x_plot = np.linspace(1, 10, 500)
- # 注意下面的 tensor转numpy
- print('weight : ', weight, 'bias : ', bias)
- plt.plot(x_plot, (weight.numpy()*x_plot+bias.numpy()).flatten(), c='black') # 这里要转为numpy才能绘制
上面是使用PyTorch进行回归分析,这里训练了100次,可以看一下最后的效果:
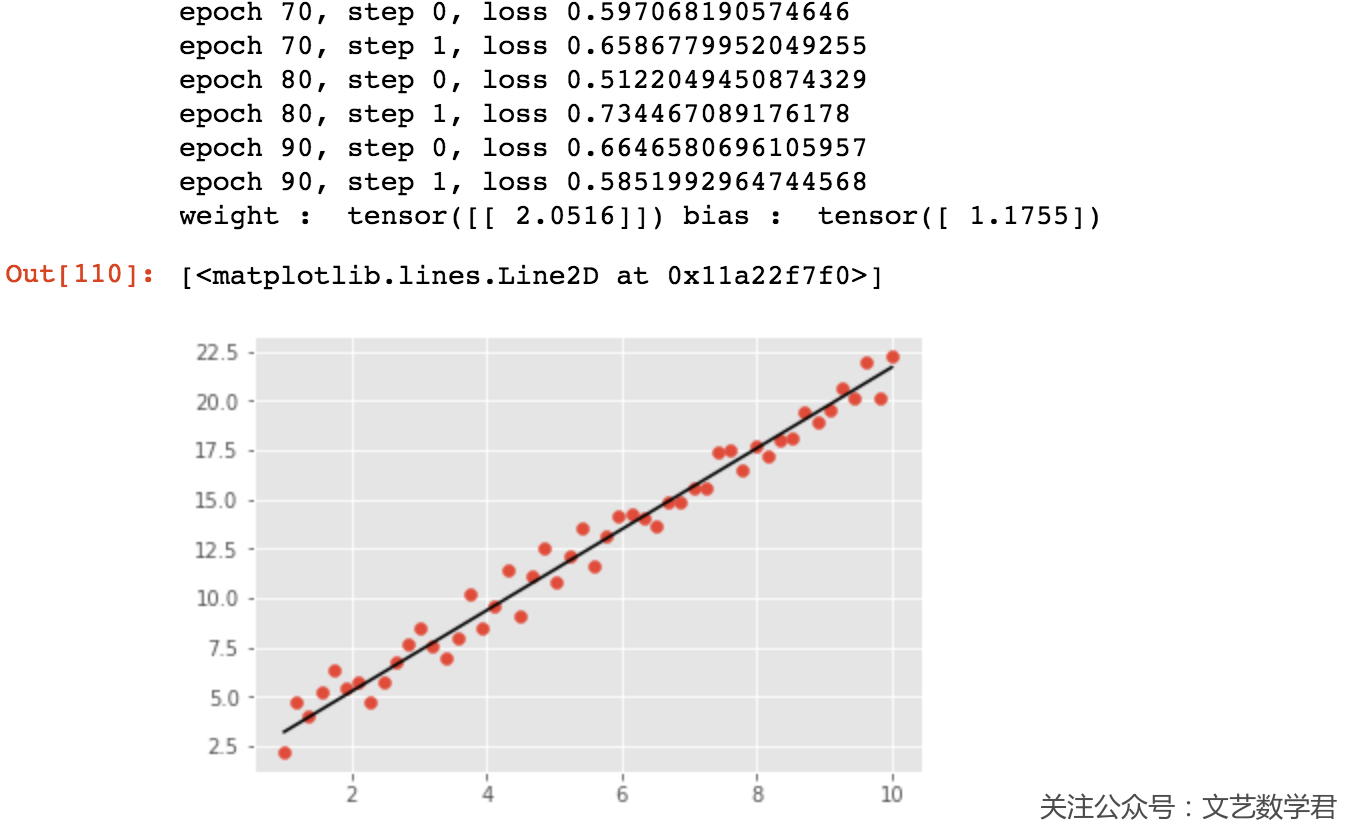
结语
到这里使用三种框架来完成线性回归的工作就已经完成了,把这三个写在一起也是为了方便我的比较和查找。
之后的话我会找一些论文里经典的网络来实现以下,顺便看看别人论文的结构之类的,就先写这么多了,之后慢慢更新。
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-













评论