Convolutional Neural Networks(CNN)介绍–Pytorch实现

王 茂南
王 茂南
王 茂南
2922
文章
75
评论
2019年3月20日16:39:04
评论 4489字阅读14分57秒
摘要主要介绍Convolutional Neural Networks(CNN)的内容， 包括为什么CNN适用于图像，卷积层与池化层的含义。逆卷积层和逆池化层的实现。文章中会使用Pytorch实现一个识别猫狗的算例。

CNN, 卷积神经网络介绍

卷积神经网络一般是由卷积层、池化层和全连接层堆叠而成的前馈神经网络结构。卷积神经网络同样使用反向传播算法进行训练。

卷积神经网络在逐层学习过程中，会逐步进行学习。第一层学习比较低层的图片结构，第二层学习依据第一层的结果学习高一级的特征，这样最后一层依据前一层学到的高级特征就能完成我们的学习任务。（如下图所示）

Convolutional Neural Networks(CNN)介绍–Pytorch实现

文章所有图片来源，都写在最后的参考资料里面了。

CNN为什么适用于图像

  1. 有时，在做图像分类的时候，不需要使用整张图片，使用关键部分即可进行检测；
  2. 关键部分在不同的图像可能会出现在不同的位置;
  3. 对图像进行放缩(重采样)，对视觉效果不会有太大的影响;
Convolutional Neural Networks(CNN)介绍–Pytorch实现

如上图，我们想要检测鸟嘴, 鸟嘴只有原始图像的一小部分. 这个就符合上面的性质一。

Convolutional Neural Networks(CNN)介绍–Pytorch实现

如上图，不同图像的鸟嘴的位置不同，符合性质二。

CNN对于图像性质的特殊设定

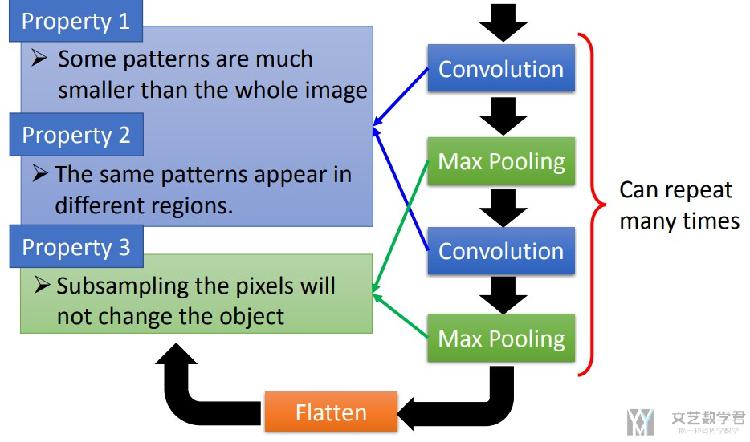
对于上面说到的三个关于图像的性质，在CNN中分别有Convolution和Pooling与之对应。

  • Convolution用来解决上面提到性质1,2
    • 每次处理图像的一部分区域
    • 会使用同一个filter来检测整个图像
  • Pooling用来解决上面提到的性质3
    • 例如MaxPooling就是在对图像的缩小
Convolutional Neural Networks(CNN)介绍–Pytorch实现

所以，当我们想要将CNN应用到图像以外的领域的时候，需要考虑是否有上面提到的三个性质，是否要对网络进行修改。如可以不使用Pooling。（这个很重要）

下面再详细解释一下卷积层和池化层。

卷积层

图片在计算机中是通过像素矩阵来进行表示的，每一个像素一个数值，范围为0-255。如下图所示，图片矩阵为499*495的矩阵。

Convolutional Neural Networks(CNN)介绍–Pytorch实现

对于彩色照片，我们通常使用RGB三个信道来进行表示，把三个信道进行叠加，就可以看到彩色的照片了。对于上面的图片，如果是彩色的，就会是(499, 495, 3)。

卷积核

内容来源：Machines that can see: Convolutional Neural Networks

首先我们来看一下卷积是如何具体进行运算的。我们有如下的图像矩阵和卷积核。

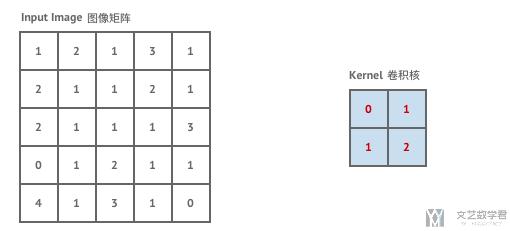
Convolutional Neural Networks(CNN)介绍–Pytorch实现

用动图来看一下卷积的过程。

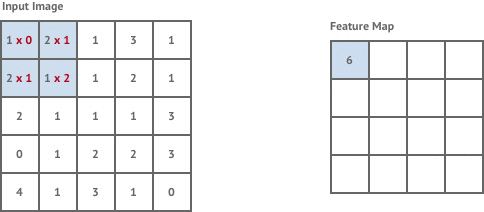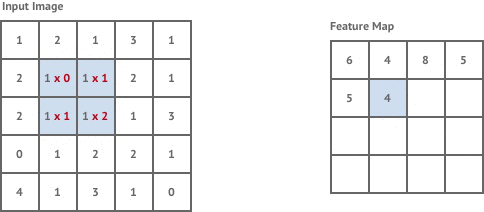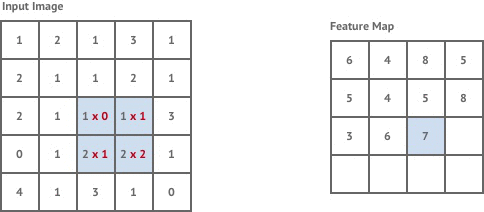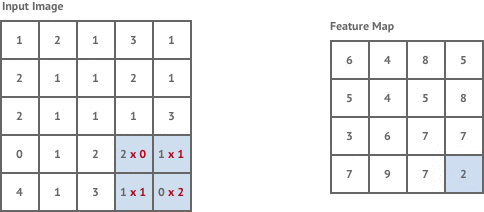
Convolutional Neural Networks(CNN)介绍–Pytorch实现

卷积的过程就是一个简单的乘法和加法的过程。如在左上角的时候，我们可以看到计算步骤为：1×0 +2×1+2×1+1×2=6。

一些特定的卷积可以提供相应的功能，如下面的边缘提取算子。详细的可以查看这个链接。图像处理--------应用卷积– 轧花与边缘检测

Convolutional Neural Networks(CNN)介绍–Pytorch实现

需要注意的是，卷积核中的数字就是网络需要学习的参数。

卷积步长

在上面的动图中，卷积步长（Stride）为1。当然，我们可以设置卷积步长为2。步长变大会提升效率。

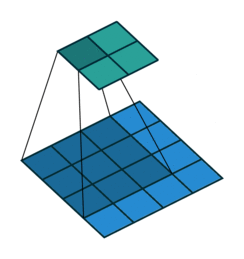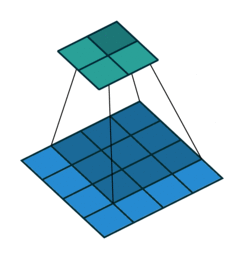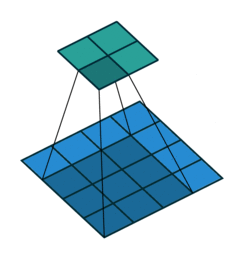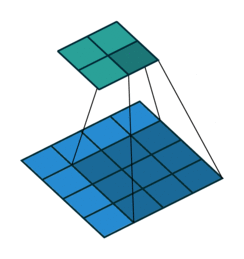
下面是卷积步长为1的情况：

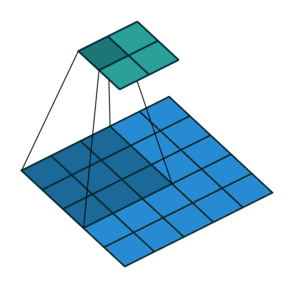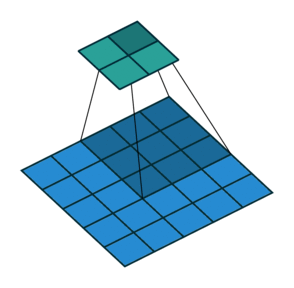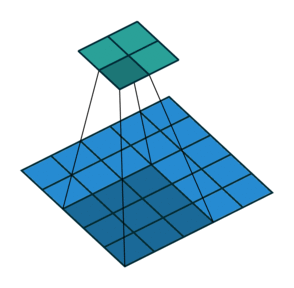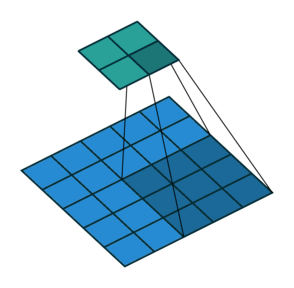
Convolutional Neural Networks(CNN)介绍–Pytorch实现

下面是卷积步长为2的情况：

Convolutional Neural Networks(CNN)介绍–Pytorch实现

边距扩展

边距扩展的由来是因为我们需要控制输出的矩阵的大小。我们会发现，随着卷积步长的增大，输出矩阵在持续变小，于是就有了边距扩展（Padding）的操作。

我们来看一个例子，Half Padding。Half Padding 也叫 Same Padding，它希望得到的输出矩阵尺寸与输入尺寸一致。下图即为我们对5×5的输入矩阵外围补上一圈0后，与3×3的卷积核做卷积运算，最终依然得到5×5的输出矩阵的过程。

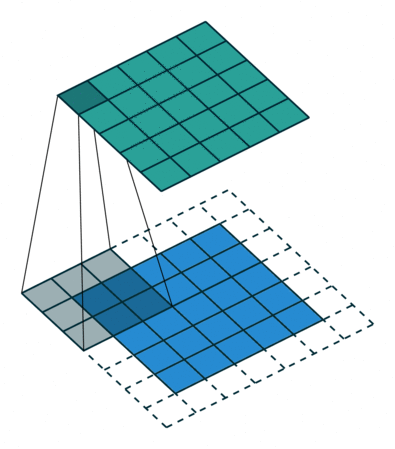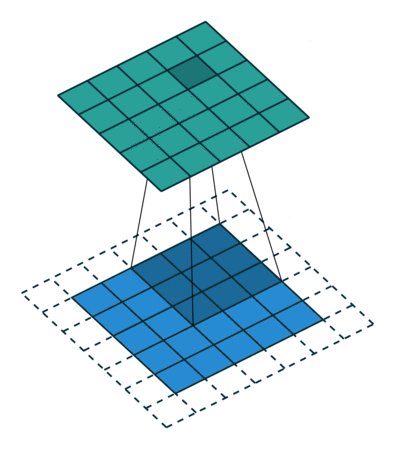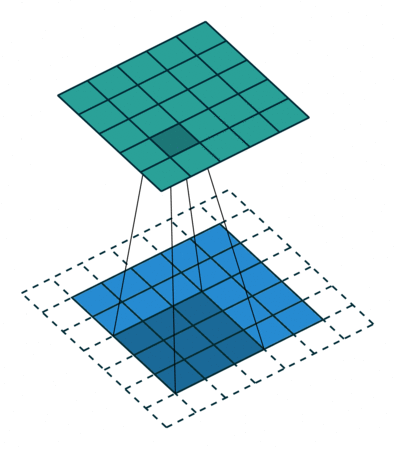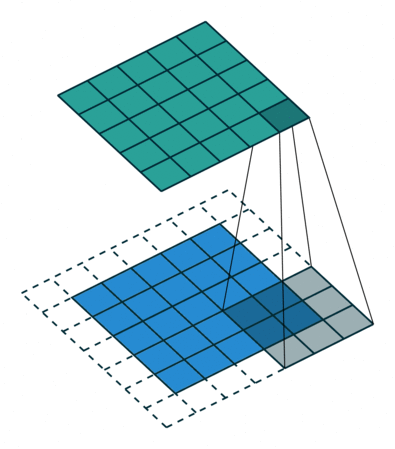
Convolutional Neural Networks(CNN)介绍–Pytorch实现

在Pytorch中，padding的计算可以通过下面的公式来得到：

Convolutional Neural Networks(CNN)介绍–Pytorch实现

高维多卷积核过程

对于彩色图片的三维图像矩阵，如m×n×k的矩阵，我们可以选取a×b×k的卷积核。下面我们举一个例子。（彩色图片的卷积核相当于是一个立方体）

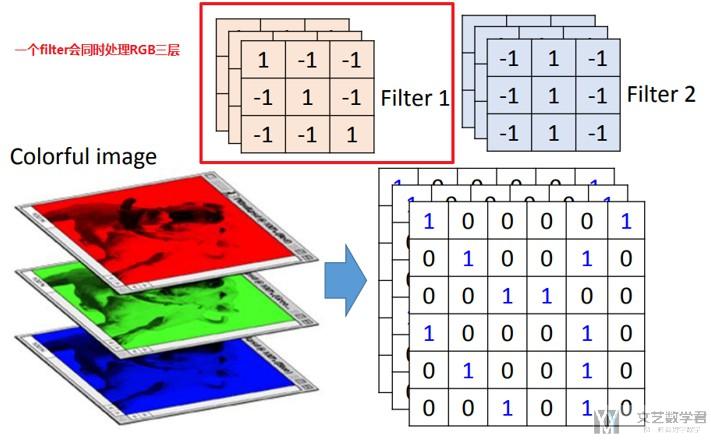
Convolutional Neural Networks(CNN)介绍–Pytorch实现

下面输入矩阵为5×5×3，padding=1，stride=2；两个卷积核为3×3×3（相当于是两个正方体, 做卷积操作的时候会对所有的通道同时进行操作）；进行卷积后，得到了3×3×2的输出矩阵。（注意下面在进行计算的时候需要加上b0）

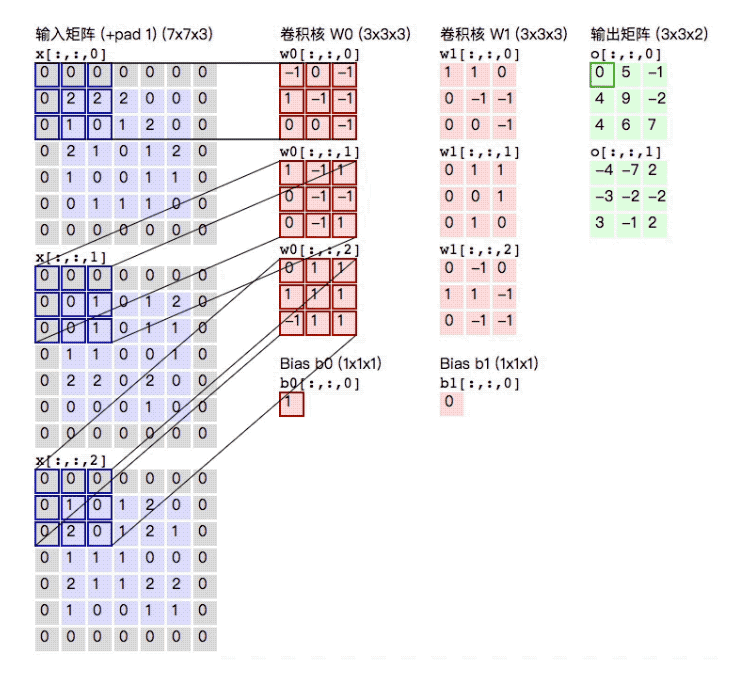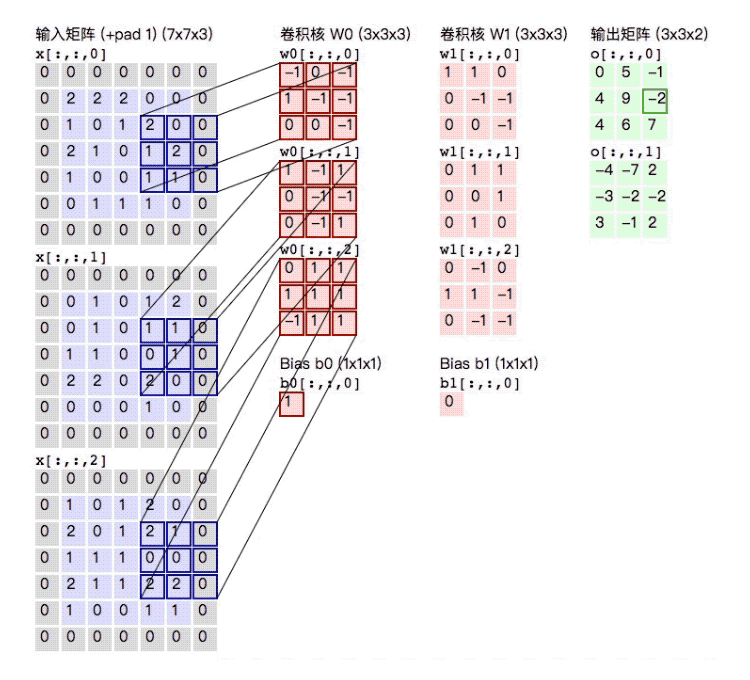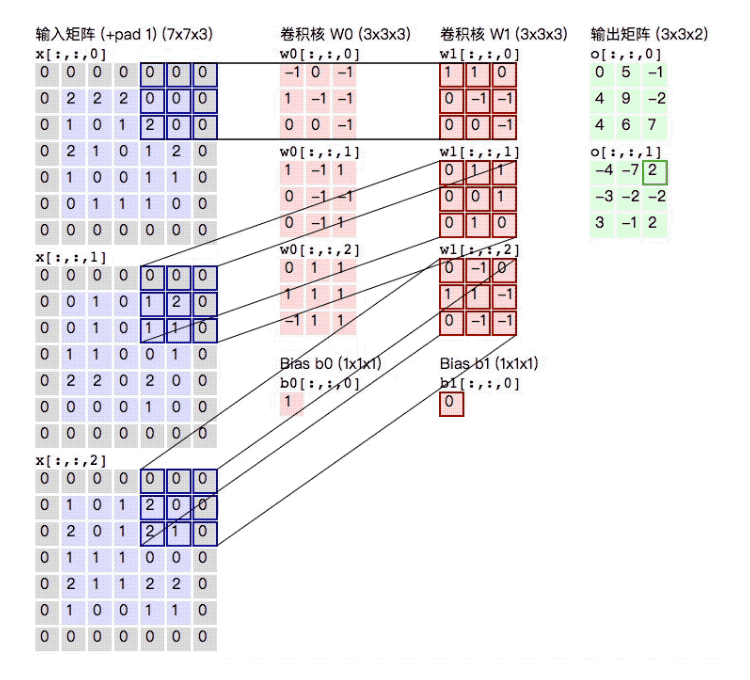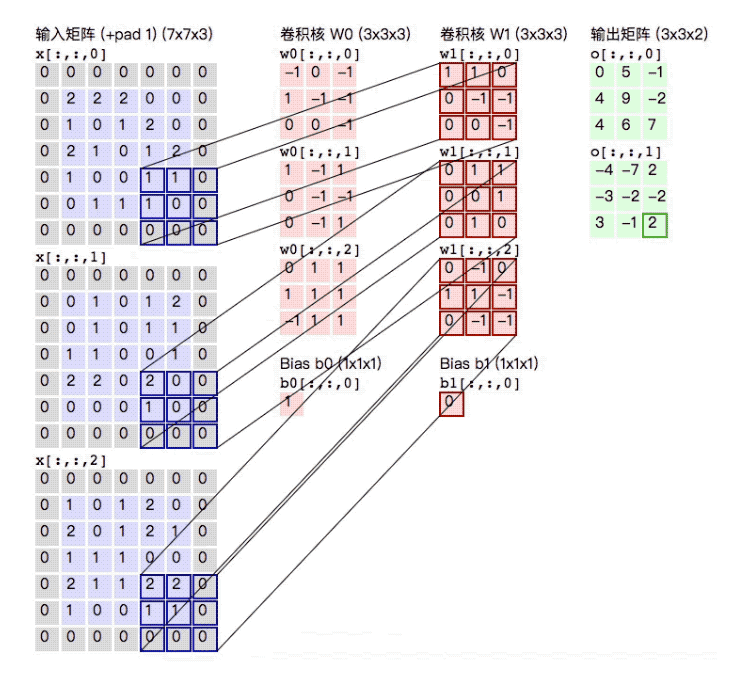
Convolutional Neural Networks(CNN)介绍–Pytorch实现

下面来看一下计算卷积中使用的参数个数. 如果卷积大小是3, input channel是3, output channel是3. 于是我们可以将一个卷积相成一个三维的正方体, 每次计算3×3×3大小的位置. 因为output channel是3, 所以有3个这样的正方体, 所以参数个数是3×3×3×3=81个. 注意这里是没有bias的.

  1. a = nn.Conv2d(3, 3, 3, 1, 0, bias=False)
  2. sum(p.numel() for p in a.parameters())
  3. """
  4. 81
  5. """

还有一类卷积, 他的卷积核大小是1×1, 他的主要目的是改变通道的个数. 例如下面的图所示, 将三通道转换为2通道.

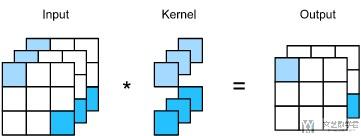
Convolutional Neural Networks(CNN)介绍–Pytorch实现

同样看一下卷积大小是1的时候参数的个数. 和上面的思路类似, 参数计算为1×3×3=9.

  1. a = nn.Conv2d(3, 3, 1, 1, 0, bias=False)
  2. sum(p.numel() for p in a.parameters())
  3. """
  4. 9
  5. """

 

PyTorch中的实现

在PyTorch中，分别会有nn.Conv1d，nn.Conv2d，nn.Conv3d，分别对应1D, 2D, 3D卷积，可以看下面的图片。

一维卷积

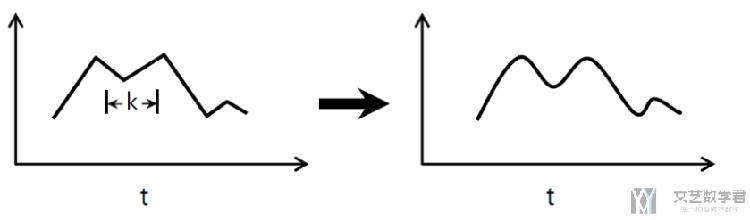
Convolutional Neural Networks(CNN)介绍–Pytorch实现

二维卷积

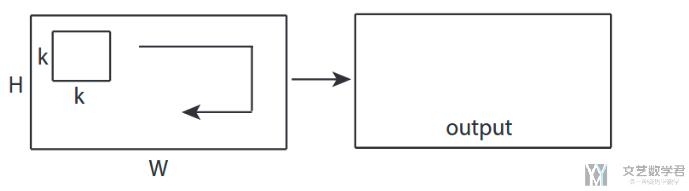
Convolutional Neural Networks(CNN)介绍–Pytorch实现

三维卷积

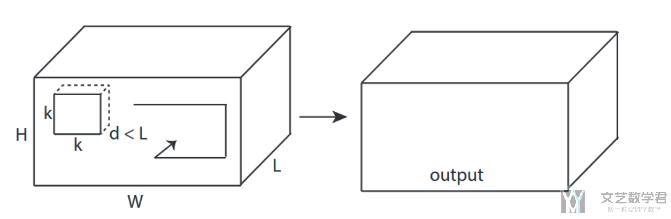
Convolutional Neural Networks(CNN)介绍–Pytorch实现

参考链接 : CNN中的1D，2D和3D卷积是什么意思？

池化层

上面介绍了卷积层，接着介绍卷积神经网络中另一个非常重要的层，也就是池化层。池化操作其实就是降采样操作过程。我们都知道，图片是一个非常大的训练数据，所以想达到很好的训练性能，只有卷积层是不够的。池化层通过降采样的方式，在不影响图像质量的情况下，压缩图片，达到减少训练参数的目的。

需要注意的是，往往在几个卷积层之后我们就会引入池化层，池化层没有需要学习的参数，且池化层在每一个深度上独立完成，就是说池化后图像的纵深保持不变。下面介绍两种常用的池化方式（直接看图就可以明白，就不解释了）。

最大值池化

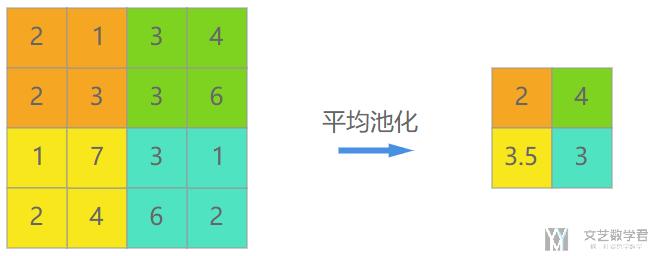
Convolutional Neural Networks(CNN)介绍–Pytorch实现

平均值池化

Convolutional Neural Networks(CNN)介绍–Pytorch实现

我们可以看一下池化后图片的效果，其实在大体上我们还是可以进行识别的。

这是原始的图像。

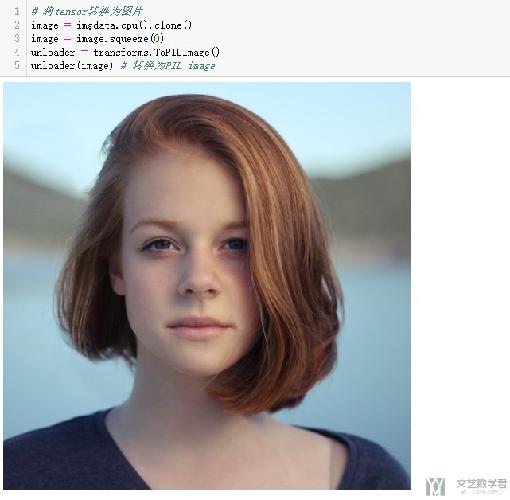
Convolutional Neural Networks(CNN)介绍–Pytorch实现

下面是使用MaxPooling之后的效果。

Convolutional Neural Networks(CNN)介绍–Pytorch实现

下面是使用AvgPooling之后的效果。

Convolutional Neural Networks(CNN)介绍–Pytorch实现

其实简单的理解，Pooling就是对图像实现了放缩的操作。

Unpool与ConvTransposed

关于逆卷积和逆池化的过程，可以查看下面的链接的MaxPool2d 与 MaxUnpool2d和ConvTransposed2d使用介绍的部分。

链接地址：PyTorch使用记录

CNN与Fully-Connected Network的联系

下面看一下CNN与Fully-Connected Network之间的联系。

我们假设原始图像假设为33的图像，Filter为22的filter，如下图所示

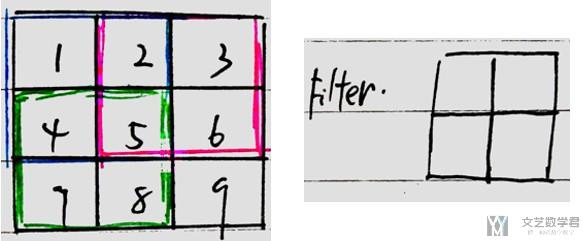
Convolutional Neural Networks(CNN)介绍–Pytorch实现

上图中的1，2，3, ...表示方格的序号, 与后面的全连接网络节点的序号对应; 我们将其转换为全链接网络的形式，如下图所示，三种颜色与上面图片中的三种颜色对应。即filter移动了三次。需要注意的是，每次网络只有四个参数要训练，其他都是为0. 同时，移动的过程中, weight是共享的。

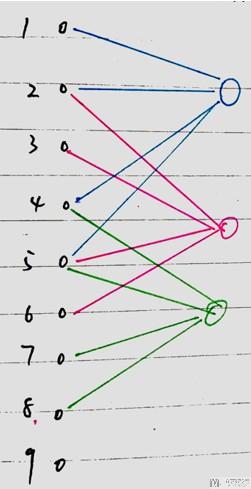
Convolutional Neural Networks(CNN)介绍–Pytorch实现

于是，我们可以得到下面的结论：

  • Convolution相当于去掉了一些weight;(参数个数减少)
  • 同时, Convolution可以实现weight的共享;

PyTorch实现

详细的链接地址如下 : Pytorch_CNN_CAT_DOG

网络结构如下所示：

Convolutional Neural Networks(CNN)介绍–Pytorch实现
  1. class cnn(nn.Module):
  2.     def __init__(self):
  3.         super(cnn, self).__init__()
  4.         # 参数的定义
  5.         # 卷积层+池化层
  6.         self.conv = nn.Sequential(
  7.             # 第一层
  8.             nn.Conv2d(kernel_size=3, in_channels=1, out_channels=32, stride=1, padding=1), # (64, 64, 32)
  9.             nn.ReLU(),
  10.             nn.MaxPool2d(kernel_size=2, stride=1), #（63, 63, 32）
  11.             # 第二层
  12.             nn.Conv2d(kernel_size=3, in_channels=32, out_channels=64, stride=1, padding=1), # (63, 63, 64)
  13.             nn.ReLU(),
  14.             nn.MaxPool2d(kernel_size=2, stride=1), # (62, 62, 64)
  15.             # 第三层
  16.             nn.Conv2d(kernel_size=3, in_channels=64, out_channels=128, stride=1, padding=1), # (62, 62, 128)
  17.             nn.ReLU(),
  18.             nn.MaxPool2d(kernel_size=2, stride=2)# (31, 31, 128)
  19.         )
  20.         # 全连接层
  21.         self.line = nn.Sequential(
  22.             nn.Linear(in_features=123008, out_features=128), # 31*31*128
  23.             nn.Dropout(p=0.6),
  24.             nn.Linear(in_features=128, out_features=2)
  25.         )
  26.     def forward(self, x):
  27.         x = self.conv(x)
  28.         x = x.view(x.size(0), -1) #展开
  29.         x = self.line(x)
  30.         return x

需要注意的只有padding那里的数值。如第一层我们要保持经过卷积运算后图像大小不变，利用上面的公式（在讲边距扩展的时候那里有一个式子），把kernel_size, stride, H(in), H(out)的值确定下来，就能计算padding了。

每一层输出的大小我都标注在旁边了，可以进行查看。

模型的保存于重载

第一种是只保存模型的参数：

  1. # 只保存模型的参数
  2. torch.save(Cnn.state_dict(),'cats_dogs_params.pkl')
  3. # 重载模型参数
  4. Cnn.load_state_dict(torch.load('cats_dogs_params.pkl'))

第二种是保存整个模型：

  1. # 保存整个模型
  2. torch.save(Cnn, 'cats_dogs_params.pth')
  3. # 加载整个模型
  4. model = torch.load('model.pth')

其余过程都类似，具体可以看github仓库中的文件。

参考文章

PyTorch文档 : PyTorch文档

The Course of Hung-yi Lee : 台大课程

非常好的入门的一个教材：实验楼机器学习

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2019年3月20日16:39:04
  • 转载请务必保留本文链接：https://mathpretty.com/10192.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: