这一篇文章我们来讲一下神经网络中的反向传播算法,我们看一个具体的例子来看一下反向传播算法是如何工作的。
我是参考的这篇文章来进行举例的,一文弄懂神经网络中的反向传播法——BackPropagation,但是原文没有用矩阵的方式来表达,我想重新用矩阵的方式来表达一遍,然后就把步骤在这里记录一下。
更新,重新写了一下, 可以参考这篇文章 : Backpropagation(反向传播)方法介绍
这一篇会写得更加详细一些。这一篇可以不用往下看了. 这一篇就不更新了。
更多关于深度学习的可以参考这篇介绍,机器学习文章总结,之后更新都会写在这里。
文章目录(Table of Contents)
系数初始化
好了,下面就开始讲一下算例。
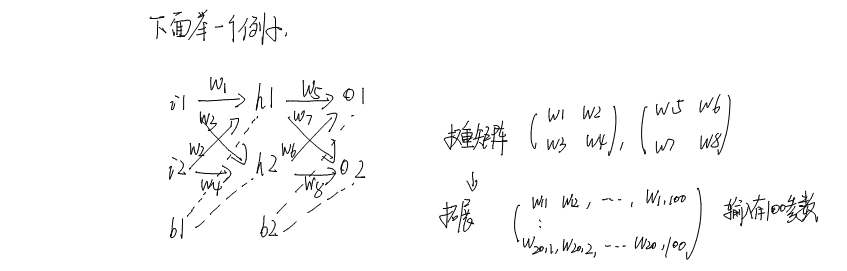
这个网络就是上面的链接里是一样的,我们进行初始化,为了最后比对我们计算是否正确,我们就使用和原文一样的初始化数据。
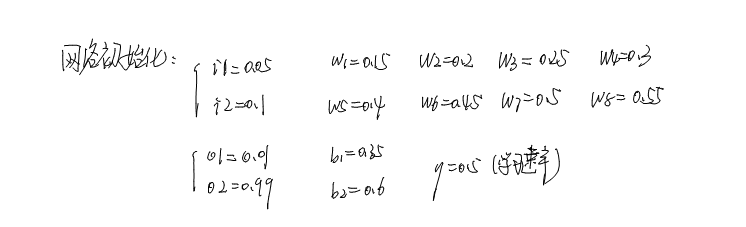
为了方便计算,我们就使用Mathematic来验证我们计算的结果,我们首先先初始化一些参数。
- w1 = 0.15;
- w2 = 0.2;
- w3 = 0.25;
- w4 = 0.3;
- w5 = 0.4;
- w6 = 0.45;
- w7 = 0.5;
- w8 = 0.55;
- i1 = 0.05;
- i2 = 0.1;
- b1 = 0.35;
- b2 = 0.6;
- o1 = 0.01;
- o2 = 0.99;
前向传播算法
接下来我们看一下向前传播的算法:

同样的,我们使用Mathematica来实现向前传播算法:
- {{netH1}, {netH2}} = {{w1, w2}, {w3, w4}}.{{i1}, {i2}} + {{b1}, {b1}}
- >> {{0.3775}, {0.3925}}
- {{outH1}, {outH2}} = 1/(1 + E^(-({{netH1}, {netH2}})))
- >> {{0.59327}, {0.596884}}
- {{netO1}, {netO2}} = {{w5, w6}, {w7, w8}}.{{outH1}, {outH2}} + {{b2}, {b2}}
- >> {{1.10591}, {1.22492}}
- {{outO1}, {outO2}} = 1/(1 + E^(-({{netO1}, {netO2}})))
- >> {{0.751365}, {0.772928}}
放一张完整的图片

到这里先前传播算法就结束了,接下来要计算误差和进行反向传播了。
反向传播算法
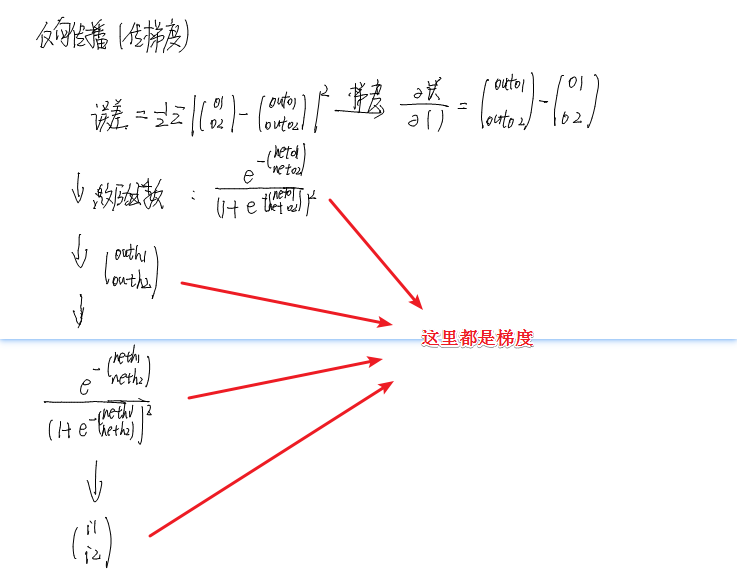
我们首先按照上面的图把每一步的梯度计算出来
- dx1 = {{outO1}, {outO2}} - {{o1}, {o2}}
- >> {{0.741365}, {-0.217072}}
- dx2 = (E^(-({{netO1}, {netO2}})))/(1 + E^-({{netO1}, {netO2}}))^2
- >> {{0.186816}, {0.17551}}
- dx3 = {{outH1}, {outH2}}
- >> {{0.59327}, {0.596884}}
- dx4 = (E^(-({{netH1}, {netH2}})))/(1 + E^-({{netH1}, {netH2}}))^2
- >> {{0.241301}, {0.240613}}
- dx5 = {{i1}, {i2}}
- >> {{0.05}, {0.1}}
我们放一张完整的图片

参数更新
下面我们就要开始更新参数了,下面我们看一下更新w5,w6,w7,w8的参数的步骤
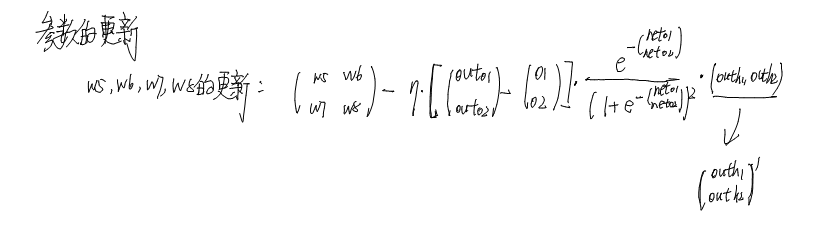
- {{w5, w6}, {w7, w8}} - 0.5*(dx1*dx2).Transpose[dx3]
- >> {{0.358916, 0.408666}, {0.511301, 0.56137}}
接着我们更新w1,w2,w3,w4
- {{w1, w2}, {w3, w4}} - 0.5*( Transpose[{{w5, w6}, {w7, w8}}].(dx1*dx2)*dx4).Transpose[dx5]
- >> {{0.149781, 0.199561}, {0.249751, 0.299502}}
完整过程
最后我们看一下一个完整的过程吧,还是用我的手写推导:
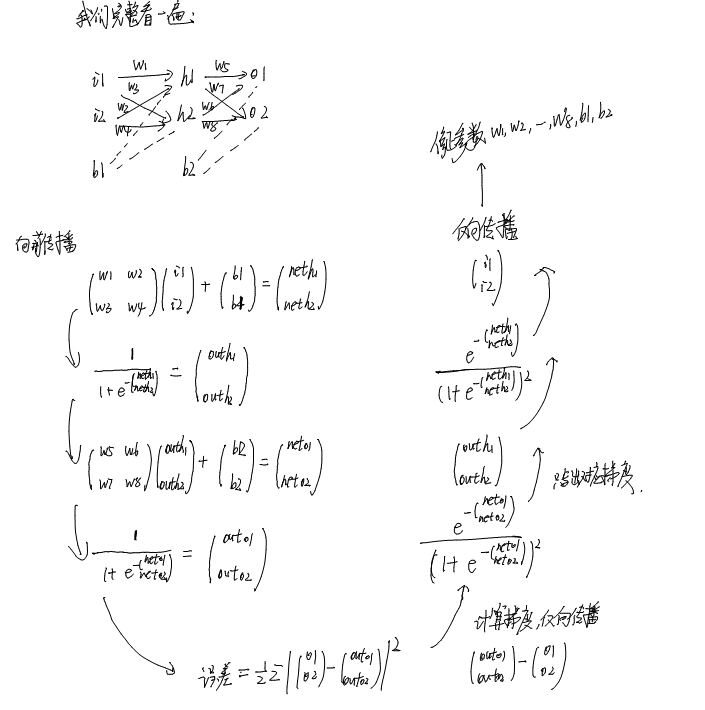
一些话
到这里,我们就完成了一个例子的推导。所有的公式都是拿手写的,然后计算使用Mathematica来代替,感觉最近Mathematica有点失宠了,我已经好久没用她来做什么好玩的事情了。
最近自己正在整理电脑上的一些文件,之前还发了两篇之前参加建模留下的文件的照片。最近应该会把一些关于Mathematica的文件整理一下的,之后的话看看要看一些什么东西。
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-













评论