Pytorch实现Deep Q-Learning(Cliff Walking PlayGround)

王 茂南
王 茂南
王 茂南
3084
文章
75
评论
2020年8月12日07:53:45
评论2 7615字阅读25分23秒
摘要这一篇简单介绍使用Pytorch在环境Cliff Walking PlayGround上实现Deep Q-Learning. 也是对官网教程的详细说明.

简介

这一篇是参考自Pytorch官网的教程, REINFORCEMENT LEARNING (DQN) TUTORIAL. 我对其中做了一些简化. 在原实验中是使用了CartPole-v0的环境, 但是因为在线上环境Google Colab里面无法渲染图像, 所以我选择使用Cliff Walking PlayGround.

这一篇主要概述一下使用Pytorch实现Deep Q-Learning的过程. 里面暂时不会涉及原理的介绍, 只会有DQN的整体算法流程.

参考资料

 

DQN的整体步骤

在讲具体的实现之前, 我们先来简单聊一下DQN的训练步骤. 在DQN中会有两个网络, 分别叫做Policy Network和Target Network. 这两个network的结构是一样的, 只有网络的参数不同.

  • Policy Network
    • Policy Network会产生action
    • Policy Network会在每一轮进行更新.
  • Target Network
    • 每过N轮, Target Network会直接拷贝Policy Network的参数.

下面是DQN的算法流程.

  • 用Policy Network生成每一个action的概率, 接着根据epsilon-greedy策略选取一个action.
  • 执行action, 将得到的{state, action, next_state, reward}存入memory中.
  • 从memory中选取一个mini-batch进行训练.
  • 按照下面的式子计算Loss, 并进行Policy Network的参数更新. (每N轮再更新Target Network)
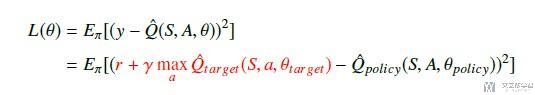
Pytorch实现Deep Q-Learning(Cliff Walking PlayGround)

 

Pytorch实现DQN

环境介绍

在这次实验中, 我们使用的是Cliff Walking PlayGround, 环境如下所示:

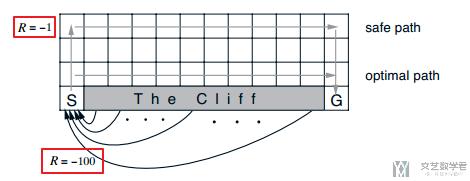
Pytorch实现Deep Q-Learning(Cliff Walking PlayGround)

一共有48个状态, 每次环境返回的是state的编号, 也就是现在在哪个格点上面. 为了作为网络的输入, 我们将state转换为one-hot编码. 共48维. 来作为网络的输入. 下面是state转one-hot向量的函数.

  1. def get_screen(state):
  2.     """这里我们就用state来作为例子, 不直接使用截图了
  3.     """
  4.     y_state = torch.Tensor([[state]]).long()
  5.     y_onehot = torch.FloatTensor(1, 48) # 产生位置
  7.     # In your for loop
  8.     y_onehot.zero_() # 全部使用0进行填充
  9.     y_onehot.scatter_(1, y_state, 1) # 返回one-hot
  11.     return y_onehot

我们看一下例子, 假设现在在state=1上面, 查看返回的输出. 可以看到第2位上面是1, 其他位置是0.

  1. print(get_screen(1).shape)
  2. """
  3. torch.Size([1, 48])
  4. """
  6. get_screen(1)
  7. """
  8. tensor([[0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
  9.          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
  10.          0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
  12. """

 

Replay Memory的定义

在DQN中, 会有一个memory来存储之间环境生成的值, 可以被用来反复使用. 这里会记录每一次action之后的, {state, action, next_state, reward}.

通过在memory里面随机采样进行训练, 可以改善DQN训练的稳定性. 我们首先定义一个namedtuple.

  1. Transition = namedtuple('Transition', ('state', 'action', 'next_state', 'reward'))
  3. Transition(24,1,25,1)
  4. """
  5. Transition(state=24, action=1, next_state=25, reward=1)
  6. """

接着定义ReplayMemory的类, 主要实现两个函数:

  • 向memory里进行添加{state, action, next_state, reward};
  • 从memory中进行随机采样;
  1. class ReplayMemory(object):
  2.     def __init__(self, capacity):
  3.         self.capacity = capacity # 允许存储多少状态
  4.         self.memory = [] # 存入的状态 
  5.         self.position = 0 # memory的list的下标
  7.     def push(self, *args):
  8.         """Saves a transition."""
  9.         if len(self.memory) < self.capacity:
  10.             self.memory.append(None)
  11.         self.memory[self.position] = Transition(*args)
  12.         self.position = (self.position + 1) % self.capacity
  14.     def sample(self, batch_size):
  15.         return random.sample(self.memory, batch_size)
  17.     def __len__(self):
  18.         return len(self.memory)

 

定义Q Network

我们在这里使用全连接网络, 输入是48, 输出是4(对应四个action, 分别是上, 下, 左, 右). 网络的整体结构是48->24->12->4.

  1. class DQN(nn.Module):
  3.     def __init__(self):
  4.         super(DQN, self).__init__()
  5.         self.l1 = nn.Linear(48, 24)
  6.         self.l2 = nn.Linear(24, 12)
  7.         self.l3 = nn.Linear(12, 4)
  9.     def forward(self, x):
  10.         x = F.relu(self.l1(x))
  11.         x = F.relu(self.l2(x))
  12.         x = self.l3(x)
  13.         return x # Returns tensor([[left0exp,right0exp,down0exp,down0exp]...]).

我们对上面定义的网络做一下测试.

  1. model = DQN()
  2. model(get_screen(1)) # 返回的4个action的值的大小
  3. """
  4. tensor([[-0.0524,  0.0964,  0.1775,  0.1297]], grad_fn=<AddmmBackward>)
  5. """

 

动作选择函数

接着我们定义一个动作选择函数. 我们会根据Policy Network生成的动作的概率进行选择. 同时我们会希望一开始的时候探索率高一些, 之后逐渐降低. 下面是实现的是epsilon-greedy策略.

  1. def select_action(state, model, nA):
  2.     """这里是包含探索的
  3.     """
  4.     global steps_done
  5.     EPS_START = 0.9 # 初始的探索率
  6.     EPS_END = 0.05 # 最终的探索了
  7.     EPS_DECAY = 300 #进行200步骤, 到最终的探索率
  9.     sample = random.random()
  10.     eps_threshold = EPS_END + (EPS_START - EPS_END) * math.exp(-1. * steps_done / EPS_DECAY) # 计算实时探索率
  11.     steps_done += 1
  12.     if sample > eps_threshold:
  13.         with torch.no_grad():
  14.             return model(state).max(1)[1].view(1, 1) # 返回的最大动作的indice
  15.     else:
  16.         return torch.tensor([[random.randrange(nA)]], device=device, dtype=torch.long) # 随机选一个动作

 

定义训练函数

最后我们就定义总体训练的函数. 总的训练步骤就和我们上面说的是一样的. 我们做了一点点的修改, 将最后到达终点的reward修改成了100.

  1. def QNetwork(env, num_episodes, policy_net, target_net, memory, discount_factor=1.0):
  2.     TARGET_UPDATE = 10 # target网络的更新论数
  3.     BATCH_SIZE = 256
  4.     # 环境中所有动作的数量
  5.     nA = env.action_space.n # 环境的动作个数
  7.     # 记录reward和总长度的变化
  8.     stats = plotting.EpisodeStats(
  9.         episode_lengths=np.zeros(num_episodes+1),
  10.         episode_rewards=np.zeros(num_episodes+1))
  13.     for i_episode in range(1, num_episodes+1):
  14.         # 开始一轮游戏
  15.         state = env.reset()
  16.         state=get_screen(state) # 将state转换为oen-hot的tensor, 用作网络的输入.
  17.         action = select_action(state, model=policy_net, nA=nA)
  18.         for t in itertools.count():
  19.             next_state, reward, done, _ = env.step(action.detach().item()) # 执行action, 返回reward和下一步的状态
  20.             if done:
  21.                 reward = 100
  22.             reward = torch.tensor([reward], device=device) # 转为tensor
  23.             next_state_tensor = get_screen(next_state) # 转为tensor
  24.             next_action = select_action(state=next_state_tensor, model=policy_net, nA=nA) # 选择下一步的动作
  26.             # 计算统计数据(带有探索的策略)
  27.             stats.episode_rewards[i_episode] += reward # 计算累计奖励
  28.             stats.episode_lengths[i_episode] = t # 查看每一轮的时间
  30.             if done:
  31.                 next_state_tensor = None
  32.                 # 这里不能直接break, 需要进行push和状态更新
  33.             else:
  34.                 pass
  36.             # 将信息存入memory
  37.             memory.push(state, action, next_state_tensor, reward)
  39.             # 状态更新
  40.             state = next_state_tensor
  41.             action = next_action
  43.             # 模型更新
  44.             if len(memory) > BATCH_SIZE: # 首先确保memory里足够sample
  45.                 transitions = memory.sample(BATCH_SIZE)
  46.                 batch = Transition(*zip(*transitions)) # 转换为如下效果, Transition(state=(5, 1), action=(6, 2), next_state=(7, 3), reward=(8, 4))
  47.                 non_final_mask = torch.tensor(tuple(map(lambda s: s is not None, batch.next_state)), device=device, dtype=torch.bool) # 确认哪些不是终点
  48.                 non_final_next_states = torch.cat([s for s in batch.next_state if s is not None]) # 将不是None的next_state连起来
  50.                 # 下面是将几个变量都转换为batch的类型
  51.                 state_batch = torch.cat(batch.state)
  52.                 action_batch = torch.cat(batch.action)
  53.                 reward_batch = torch.cat(batch.reward)
  55.                 state_action_values = policy_net(state_batch).gather(1, action_batch) # Q(s,a)的值
  57.                 next_state_values = torch.zeros(BATCH_SIZE, device=device)
  58.                 next_state_values[non_final_mask] = target_net(non_final_next_states).max(1)[0].detach()
  60.                 # Compute the expected Q values
  61.                 expected_state_action_values = (next_state_values * discount_factor) + reward_batch
  63.                 # Compute Huber loss
  64.                 loss = F.smooth_l1_loss(state_action_values, expected_state_action_values.unsqueeze(1))
  66.                 # Optimize the model
  67.                 optimizer.zero_grad()
  68.                 loss.backward()
  69.                 # for param in policy_net.parameters():
  70.                 #     param.grad.data.clamp_(-1, 1)
  71.                 optimizer.step()
  73.             if done:
  74.                 break
  75.             if t > 500:
  76.                 break
  78.         if i_episode % TARGET_UPDATE == 0:
  79.             # target net更新参数
  80.             target_net.load_state_dict(policy_net.state_dict())
  82.         if i_episode % 50 == 0:
  83.             print("\rEpisode {}/{}. | ".format(i_episode, num_episodes), end="")
  85.     return stats

 

开始训练

最后我们训练2000个episode, 看一下最终的结果.

  1. env = CliffWalkingEnv() # 初始化环境
  3. policy_net = DQN().to(device)
  4. target_net = DQN().to(device)
  5. target_net.load_state_dict(policy_net.state_dict())
  6. target_net.eval()
  8. optimizer = optim.Adam(policy_net.parameters(), 0.002)
  9. memory = ReplayMemory(500)
  11. steps_done = 0
  13. stats = QNetwork(env, 2000, policy_net, target_net, memory, discount_factor=0.9)

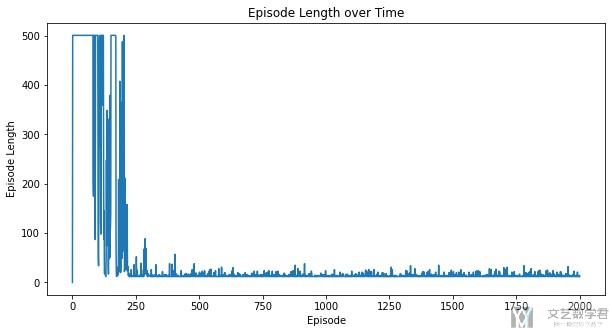
最终关于每一个episode需要走的步数变化如下所示, 大概在250轮之后模型收敛, 可以找到最优的解.

Pytorch实现Deep Q-Learning(Cliff Walking PlayGround)

  • 微信公众号
  • 关注微信公众号
  • weinxin
  • QQ群
  • 我们的QQ群号
  • weinxin
王 茂南
  • 本文由 发表于 2020年8月12日07:53:45
  • 转载请务必保留本文链接：https://mathpretty.com/12596.html
匿名

发表评论

匿名网友 填写信息

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: