文章目录(Table of Contents)
简介
这一篇文章,会简单介绍一下反向传播的相关内容。并说明一下梯度消失的原因。
数学基础
Chain Rule
这里主要介绍一下Chain Rule(链式法则),也只用到了Chain Rule.
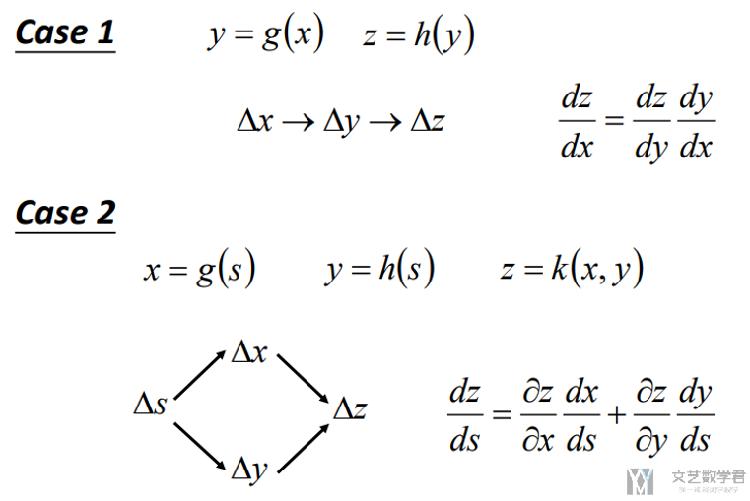
Sigmoid函数导数
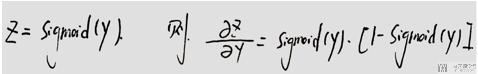
简单例子
下面这个例子,我们使用一下上面的链式法则,来尝试进行求导。
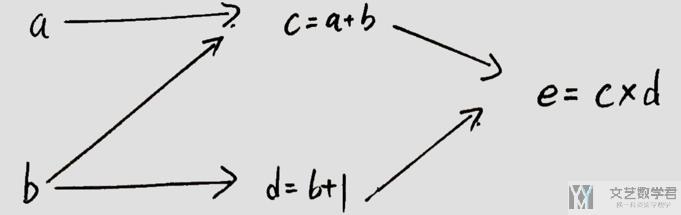
对于上面的网络结构,我们初始a=2, b=1(图中应该是b=1, 我写了a=1)。
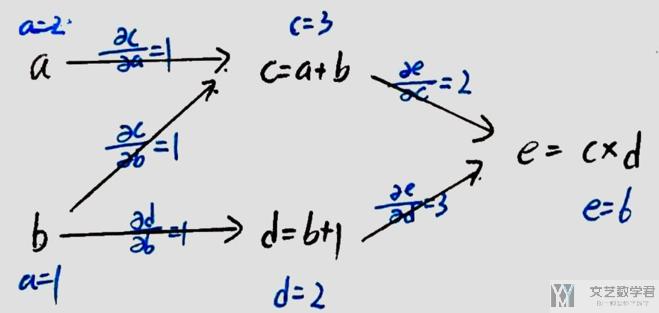
此时, 若想求e关于a和b的导数, 则可以使用链式法则,我们可以写成下面的表达式.
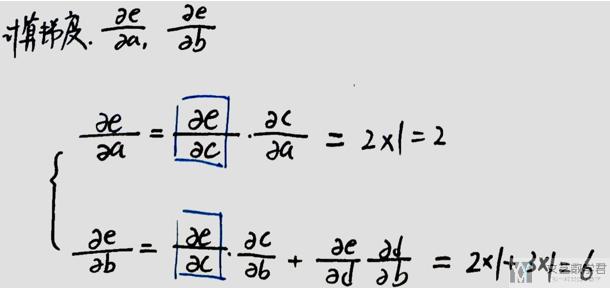
使用链式法则的一些问题
- 如求e关于b的偏导,需要找出e到b的所有路径, 正向求导比较麻烦;
- 一些值会重复使用, 具体看下面的一个例子.
全链接网络推导
我们看一个全连接网络的例子。我们想要求出loss关于w1,w2等的偏导.
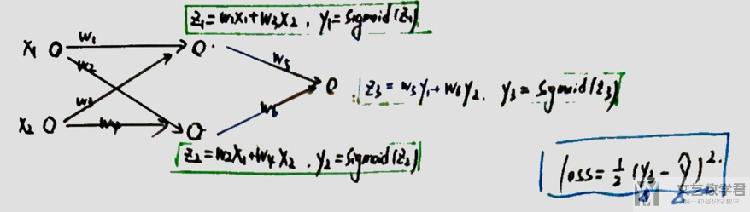
下面分别是loss关于w5和w1的偏导的求解. 我们可以看到在求loss关于w1的偏导数时, 红色部分是上面在求loss关于w5偏导时求过的值, 我们想到可以重复进行使用.
计算图与反向传播
在通常进行Backpropagation, 我们会使用计算图来进行表示, 我们看一下下面的例子.
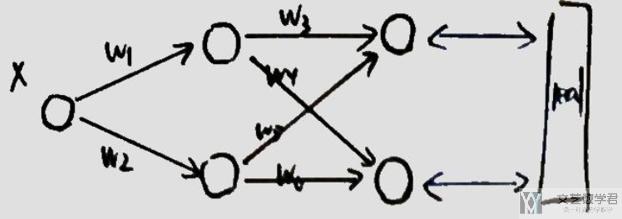
上面的网络,绘制为计算图时, 为如下的样子.
我自己重新手画一下,方便后面的书写。我们对其进行初始化与正向传播, 其中x=1, w1=(1,2), w2=((3,4),(5,6)), 图中蓝色标出的为正向传播时每一步的值.
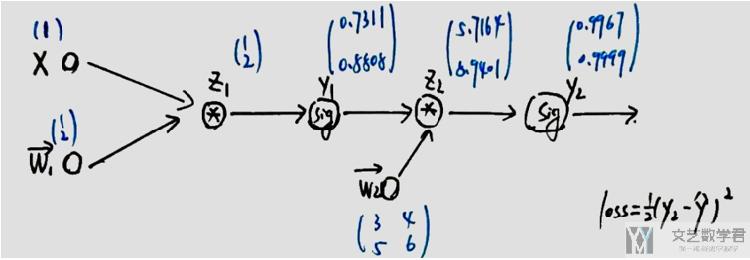
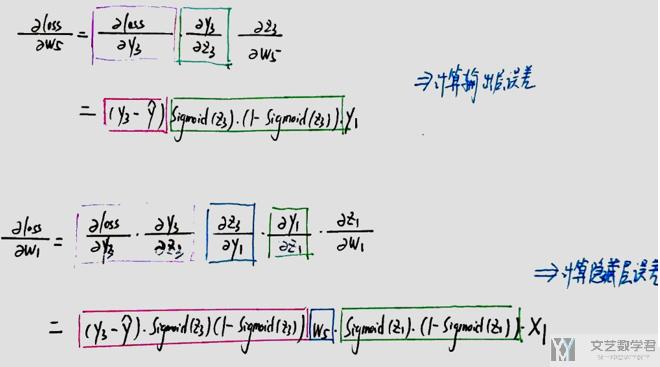
接着我们进行反向传播,即此时我们需要计算loss对于w2, w1的偏导数, 计算表达式如下所示.
求关于w2的偏导数:
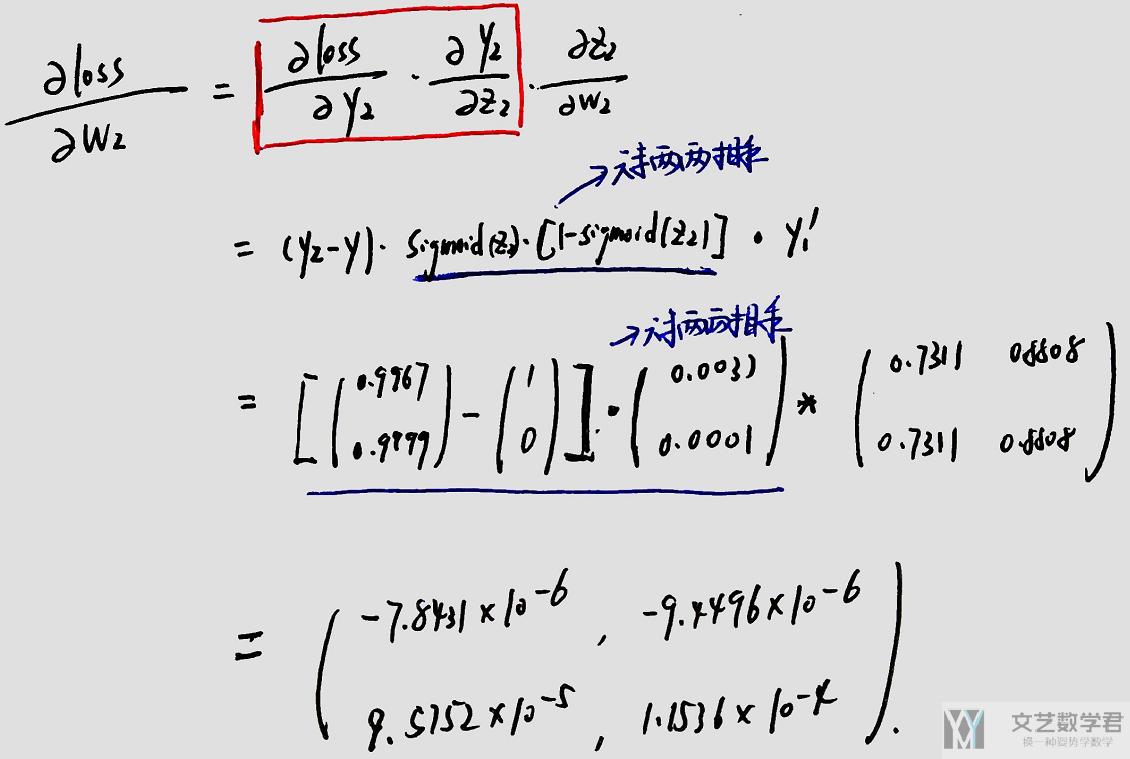
求关于w1的偏导数:
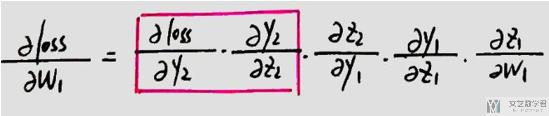
- 相当于从loss开始往前传递梯度.
- 会重复利用之前计算的梯度, 如上图中红色框出的部分.
- 如上图中红色框出的部分, 在计算loss对w2的偏导时, 计算完毕后会存储在起来(可以理解为存储在z2节点处), 下次在计算loss对w1的偏导时, 可以重复利用该值.
Pytorch实验
下面对于上面的计算图,我们使用Pytorch进行一下实验。也是记录一下如何在Pytorch中初始化网络的系数,打印梯度与系数。
网络的定义
- class NeuralNet(nn.Module):
- def __init__(self):
- super(NeuralNet, self).__init__()
- self.linear1 = nn.Linear(in_features=1, out_features=2, bias=False)
- self.linear2 = nn.Linear(in_features=2, out_features=2, bias=False)
- self.sig = nn.Sigmoid()
- def forward(self, x):
- out = self.linear1(x)
- print(out)
- out = self.sig(out)
- # y1 = out.detach().numpy().reshape(2,1)
- print(out)
- out = self.linear2(out)
- print(out)
- out = self.sig(out)
- # y2 = out.detach().numpy().reshape(2,1)
- print(out)
- # 可以自己尝试自己写一下梯度的计算
- # grad = np.dot(np.dot(np.dot(y2-np.array([[1],[0]]),y2.T),np.array([[1],[1]])-y2),y1.T)
- # print(grad)
- return out
初始化系数
首先查看一下网络的原始的weight
- # 网络的初始化
- model = NeuralNet()
- # 原始的weight
- for num, (name, params) in enumerate(model.named_parameters()):
- print(num,params.data.shape,'\n',params.data)

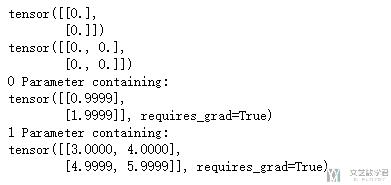
接着我们将系数设为给定的值, 方便实验.
- # 做初始化系数
- model.linear1.weight.data = torch.FloatTensor([[1],[2]])
- # model.linear1.bias.data = torch.FloatTensor([1,2])
- model.linear2.weight.data = torch.FloatTensor([[3,4],[5,6]])
- # model.linear2.bias.data = torch.FloatTensor([1,2])
- # 现在的系数
- for num, (name, params) in enumerate(model.named_parameters()):
- print(num,params)

正向传播
- # 正向传播
- input_data = Variable(torch.FloatTensor([1]))
- out = model(input_data)
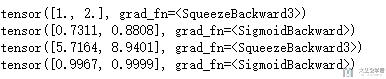
下面我们计算一下误差,target我们设置为(1,0),计算得到loss=0.4999
- # 计算误差
- label = Variable(torch.FloatTensor([1,0]))
- loss_fn = nn.MSELoss(reduction='mean')
- loss = loss_fn(out, label)
- loss
打印此时的梯度和weight,可以看到只进行正向传播并计算误差时,梯度还是没有进行计算的。
- # 打印梯度和系数
- print(model.linear1.weight.grad)
- print(model.linear2.weight.grad)
- # 现在的系数
- for num, (name, params) in enumerate(model.named_parameters()):
- print(num,params)

反向传播
接着我们进行反向传播,同时打印出现在的梯度和weight, 这里梯度就已经算出来很小了。
- # 反向传播
- loss.backward()
- # 打印梯度和系数
- print(model.linear1.weight.grad)
- print(model.linear2.weight.grad)
- # 现在的系数
- for num, (name, params) in enumerate(model.named_parameters()):
- print(num,params)

更新weight
接着就可以使用各种优化算法进行weight的更新了。(这里有与上面梯度算出来太小了, 就不把打印出来的值进行截图了)
- # 更新参数参数
- optimiser = optim.SGD(params=model.parameters(), lr=1) # 定义优化器
- optimiser.step()
梯度清零, 进行下一次计算loss
梯度清零后,在进行查看。可以看到此时的梯度为0.
- # 梯度清零
- optimiser.zero_grad()
- # 打印梯度和系数
- print(model.linear1.weight.grad)
- print(model.linear2.weight.grad)
- # 现在的系数
- for num, (name, params) in enumerate(model.named_parameters()):
- print(num,params)
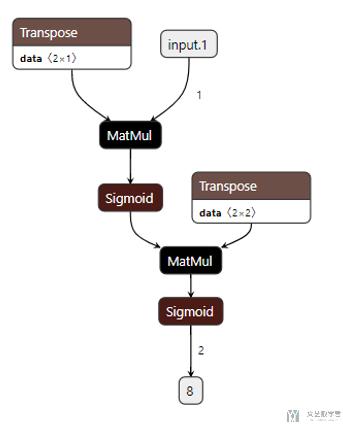
导出模型并绘图
下面我们将网络保存为onnx文件,可以进行网络结构的绘制。
- # 打印网络结构
- import torch.onnx
- # 输入测试数据
- input_data = Variable(torch.FloatTensor([1]))
- torch.onnx.export(model, input_data, "model2.onnx", export_params=True, verbose=True, training=True)
绘制工具参考这篇文章, 深度学习模型可视化-Netron
梯度消失
这一部分介绍一下在使用Sigmoid作为激活函数的情况下, 出现梯度消失的原因.
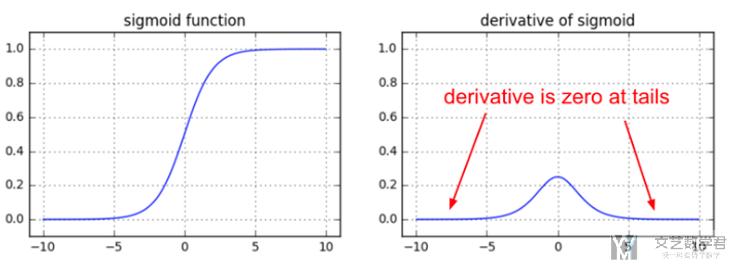
我们在上面数学基础知识部分可以看到, Sigmoid的导数可以写成z*(1-z)的样子. 有下面两个原因会导致梯度消失。
- 当y的绝对值取值较大时, Sigmoid的导数会趋于0
- 可以看下面的导数的图像
- 也可以理解为其导数为(1-z)*z, z容易趋于0或是1, 都会使导数趋于0
- 同时, (1-z)*z的最大值为1/4, 在z=1/2时取到, 也就是说每经过一个Sigmoid激活函数, 梯度会变为原来的1/4
关于Pytorch中backward的一点说明
在pytorch中backward中是可以传入参数的,这个传入的参数可以理解为偏导数的权重, 我们用下面的例子做一下解释.
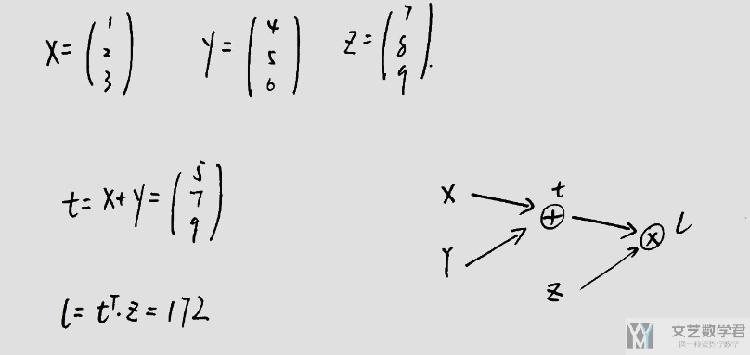
我们按照上面进行初始化值.
- x = Variable(torch.FloatTensor([[1],[2],[3]]), requires_grad=True)
- y = Variable(torch.FloatTensor([[4],[5],[6]]), requires_grad=True)
- z = Variable(torch.FloatTensor([[7],[8],[9]]), requires_grad=True)
- t = x + y
- l = torch.mm(t.reshape(1,3),z)
对于上面的式子,进行l.backward()与t.backward(z)是等价的, 我们可以认为在PyTorch中, 他最后还是对标量进行backward, 通过backward()内传入的向量作为系数.
直接进行l.backward()
- l.backward()
- # 打印梯度
- print(x.grad)
- print(y.grad)
- print(z.grad)

我们很好验证答案的正确,通过下面的式子即可进行验证.
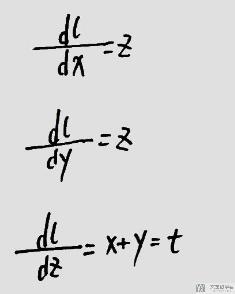
进行t.backward(z)进行反向传播
- # 这个等价于l.backward()
- t.backward(z)
- # 打印梯度
- print(x.grad)
- print(y.grad)
- print(z.grad)
这里打印的值是与上面相同的.

参考文章

直接搜索下面的关键词就可以搜索到了。
- Yes you should understand backprop[Andrej Karpathy]
- Getting Started with PyTorch Part 1: Understanding how Automatic Differentiation works
- 微信公众号
- 关注微信公众号
-

- QQ群
- 我们的QQ群号
-













评论